数3√5について述べた文として適切なものを、次のア～エから1つ選びなさい。 ア 3√5は、分母分子とも整数であるような分数で表すことができない。 イ 3√5は、循環する無限小数で表すことができる。 ウ 3√5は、2√10より小さい数である。 エ 3√5は、どんな有理数をかけても、結果は無理数である。 1とか、15とか、573とかは、きっちりした数なので、整数と言います。きっちりしてればよいので、－3とか、0だって整数です。ただし、整数は、3つに分類できます。①正の整数（自然数）②負の整数③0です。
小数と分数は別の者かというと、同じ者です。
全ての小数は、分数にすることができますね。では、全ての分数は、小数にすることができるでしょうか？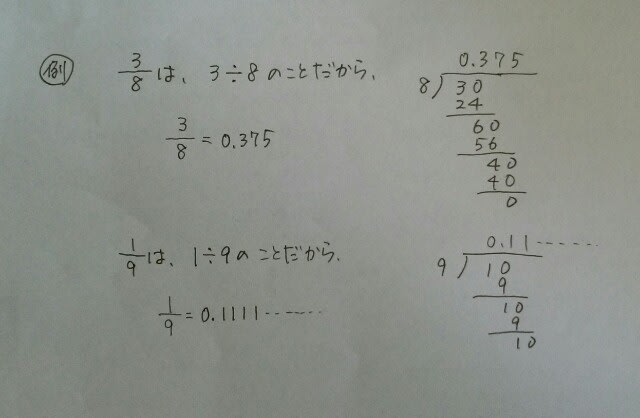
なんか、できるやつと、できないやつがありそう😩。でも、できるのです。なぜなら、どんな分数でも、それを小数に直すと、必ず循環するからです。（証明は省略）
整数、分数、小数のことを、有理数と言います。そのいずれにもあてはまらないものを、無理数と言います。代表的なものは、πと√です。ただし、√4は有理数です。なぜなら、√4は、2だからです。他にも、様々な無理数があるのですが、教養数学としては、無理数とは、πと、整数にならない√のことだなくらいで大丈夫です。 まとめます。結局、分母分子とも整数であるような分数で表すことができれば有理数、できなければ無理数です。
（注）のところですが、循環する小数は、全て、分母、分子とも整数である分数で表すことができ、その種の問題もたまに出題されています。 肢アは、言い換えると、3√5は、無理数である。となります。これは正しい。 肢イは、循環する無限小数で表すことができれば、それは分母分子ともに整数である分数になるので、有理数ということになるので、誤り。 肢ウは、
ということで誤り。 肢エは、3√5に、0という有理数を掛けると、0という有理数になるので誤り。 正解は、肢アです。
