大人の数学教室121(関数⑧)

【第8章】

(8)2次関数のグラフ

y=a(x-p)^2+q を「標準形」という。

y=ax^2+bx+c を「一般形」という。

一般形を、平方完成で標準形に変形する。

y=ax^2+bx+cのグラフ

頂点(-b/(2a),-(b2-4ac)/(4a))

軸x=-b/(2a), 原形 y=ax^2

2次関数のグラフの書き方

① 標準形 y=a(x-p)^2+q に変形する。

② 頂点(p,q) を取る。

③ 頂点を原点と思って、y=ax^2 のグラフを描く。

④ y 切片の座標を書く。(x=0 のy の値)

⑤ x 切片の座標を書く。(y=0 のx の値)

(※⑤ は必要に応じて書く。)

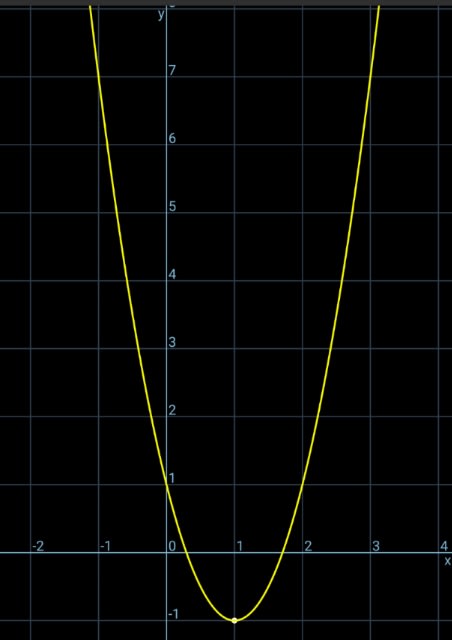
例)y=2x^2-4x+1 =2(x-1)^2-1 のグラフ

頂点(1,-1), 軸の方程式 x=1,

原形 y=2x^2