「NHK」による東京都の新型コロナウイルスの感染状況のデータをもとに、定点観測後の感染者数（推定値）の緩やかな推移からみて、今後の感染者数を今までの経験的な予測（推定式）に当てはめると、楽観的かも知れませんが緩やかに増加すると思われますので、注意してその推移を見守りたいと思います。
東京都における新型コロナ（COV-ID19）の感染者数（1週間単位）の推移
感染者数（1週間平均）の集計は2020年3月17日から3月23日の1週間の平均感染者数を第1週として現在まで163週までの約38ｶ月の推移を図１に示した。そのピークの周期は112日～182日であった。
第8波のピークは約145週当たり（2023年12月23日～30日）であり、図１の様に第7波に比べると小さかった。そして、
2023年5月８日からは、第5類になり数々の施策が変更される。
そこで、
５類移行後の感染者数の推移を今までの自然的な循環変動をもとに統計的に予測してみた（図2）。
楽観的・希望的な予測では図2の青色点線のように緩やかに推移すると思われるが、赤色点線のように急増する危険もあるので、今後（連休明けの5月8日以降）の推移に注目したいと思っている。
これは、
あくまでも個人的な推論に過ぎないことに留意して頂きたい。
図1 感染者数の推移
図2 感染者数の予測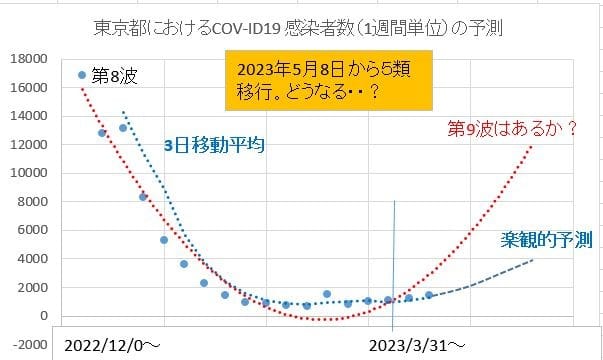
統計技術：第8章 要約統計量による効果量の計算(続き)
第8章-5：要約統計量（Summary）による効果量(続き)
下記URL（UCCS：Free Online Calcultoer）から、
https://www.psychometrica.de/effect_size.html
「#11. Effect size calculator for non-paraetric tests Mann-Whitney, Wilcoxon and Kruskal Wallis-H」を選択し、
代表的なノンパラメトリック検定の効果量を求めてみましょう。
図1 「#11」の画面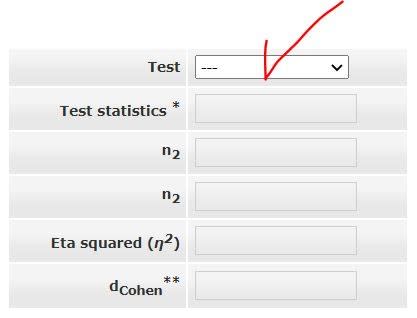
ここでは、η2 を計算するために、ウィルコクソンの符号順位検定、Mann-Whitney-U または Kruskal-Wallis-H の検定統計量から効果量を知ることができます。
赤矢印から「Test」方法を選択します。
「Test」方法は次の通りです。
・ Mann-Whitney-U
・ Wilcoxon-W → Wilcoxon signed-rank test（対応のある２群の検定）
・ Kuraskall-Wallis-H
簡単な例題「Gooブログ：統計のコツのこつ(34)」でやってみましょう。
https://blog.goo.ne.jp/k-stat/e/5902206eb2209b533f99ec160f0d6a7a
● 「マンーウイットニー順位のU検定の方法(Mann-Whitney-U test)」です。
図2 「Mann-Whitney-U」のための例題
このデータの検定結果は次の通りです。
U値＝89
ｐ値＝0.00278
ｎ１＝20、 ｎ２＝20
よって、下記（図3）のように入力します。
図３ 入力と出力の画面
「Eta squared(η^2)＝0.225 → Eta（η）＝√0.225≒0.47 （Eeffect size）」となります。
次に、
● 「ウイルコックスンの符号順位和検定の方法(Wilcoxon signed rank test)」（対応のある２群の有意差検定）です。
簡単な例題「Gooブログ：統計のコツのこつ(35)」でやってみましょう。
https://blog.goo.ne.jp/k-stat/e/4d607c86ceb4c03c8d3fea2991a2ad49
図４ 「Wilcoxon-W」のための例題
このデータの検定結果は次の通りです。
W値＝182
Ｚ値 ＝3.485892
P値＝0.00049
N＝19
ここではＺ値を用い、下記（図５）のように入力し効果量（η^2）を求めてみましょう。
図５ 入力と出力の画面
「Eta squared(η^2)＝0.64 → Eta（η）＝√0.64＝0.8（Eeffect size）」となります。
なお、
商用統計ソフトでは、「Rank-Biserial Correlation Coefficient 」（双列相関係数）で表している場合があります。
例えば、
「Wilcoxon signed rank test」の場合だと、
Rank-Biserial Correlation Coefficient≒0.92 となります。
次に、
●「クラスカル-・ウォ-リスの検定（Kruskal-Wallis-H test）」です。
簡単な例題「Gooブログ：統計のコツのこつ(38)」でやってみましょう。
https://blog.goo.ne.jp/k-stat/e/9e6499b621d713d75832ae004f14b784
図６ 「Kruskal-Wallis-H」のための例題
このデータの検定結果は次の通りです。
H値＝10.312
P値＝0.0058
N＝18
よって、下記（図7）のように入力します。
図7 入力と出力の画面
「Eta squared(η^2)＝0.554 → Eta（η）＝0.744（Eeffect size）」となります。
***
統計技術は終了します。
執筆は途中から情報統計研究所（アシスタントの”KUMI”）が担当しました。
統計技術：第8章 要約統計量による効果量の計算(続き)
第8章-4：要約統計量（Summary）による効果量(続き)
引き続き、
下記URLのUCCS（Free Online Calcultoer）を使って効果量（ES：Effect Size）を求める方法の紹介です。
https://www.psychometrica.de/effect_size.html
上記URLから、下記を選択してみて下さい。
#6. Computation of d from the F-value of Analyses of Variance (ANOVA)
ここでの効果量は、２群のANOVA test における統計量（Ｆ比）を用いて、独立したサンプル（Independent t-test）の場合と同じように効果サイズを計算するものです。
分散分析 (ANOVA) から効果サイズを解釈するのは総分散で説明された比率分散を反映する"η2 "（相関比：イータの2乗）です。この比率は、直接 d に変換されています。
それでは、簡単な例題でやってみましょう。
図１ ANOVA test 用の仮想データ（2つのmethod での評価の違い）
図２ 一元配置分散分析表（Excel の結果）
図３ 上記の「#6」から求めた効果量
ANOAVのF値から求めた効果量（ES)=1.243 でした。
このES値は、下記の方法と一致します。
#1. Comparison of groups with equal size.
#2. Comparison of groups with different sample size.
文責：
ISL assistant staff "KUMI"
次に続く！
統計技術：第8章 要約統計量による効果量の計算(続き)
第8章-3：要約統計量（Summary）による効果量(続き)
引き続き、
下記URLのUCCS（Free Online Calcultoer）を使って効果量（ES：Effect Size）を求める方法の紹介です。
https://www.psychometrica.de/effect_size.html
上記URLから、下記を選択してみて下さい。
#5. Calculation of d and r from the test statistics of dependent and independent t-tests.
ここでの効果量は、スチューデント t 検定などの仮説検定からの検定統計量を使用して取得することもできます。独立したサンプル（Independent t-test）の場合、結果は本質的に効果サイズの計算「#2 」と同じです。
例題は、
「統計のコツのこつ（31）」の要約統計量（summary data）を用いてみましょう（下記URL）。
https://blog.goo.ne.jp/k-stat/e/3ce0391051242c38d99a3a925be39d22
Summary data は次の通りです。
...........mean.......sd..........n........t-value
A 群....122.5......10.85.....30.......3.3062
B 群....133.4......12.25.....20
そでれは、上記「#5」を選択し、上記のsummary data を図１のように入力してみましょう。
図１ 「#5」(independent の場合)の入力と出力結果
Effect Size d = 0.954 となっており、
この値は、もともと、"Hedges" と "Olkin" は 修正された効果の大きさ "d" とも呼んだようで、いまだに混乱しているようです。
ここでの効果量は 1980 年代初頭から "g" と呼ばれており、最初に修正措置を提案した著者 Glass (Ellis, 2010) に由来しています。
このロジックに従って、"gHedges" は "g" ではなく" h" と呼ぶ必要がありまが、 通常、これは単純に "dCohen" または "gHedges" と呼ばれ、修正された測定値であることを示しています。
近似的に次式により"Cohen's d"を知ることができます。
d= t* sqrt(1/n1+ 1/n2)= 0.954
次に、
図１の「Mode of testing」で「dependent」を選べば、対応のあるｔ検定（Paired t-test）の効果量を知ることができます。
Summary data は次の通りです。
............mean.......sd..........n........t-value
Pre......207.93.....28.56.....15........6.6897
Post.....197.........24.39
図2 「#5」(dependent の場合)の入力と出力結果
例題（図１）の原データは図3のとおりです。
図３ 例題の原データ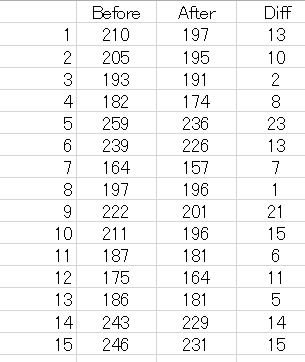
原データから計算した結果は図４のとおり、Summary の結果と一致しています。
図4 原データから計算した結果
"Free Online Calculator"(Statistics Kingdom)の結果。
しかし、
"summary data" による計算は、近似的な計算がなされている場合が多く、また、計算上の丸めなどで、必ずしも正確とは言えない場合がありますので、使用に当たってはご注意下さい。
次回の続く！
文責：
ISL assistant staff "KUMI"