東京都における新型コロナ感染者数の推移（１週間当たり）
2020年3月17日以降における東京都の新型コロナ感染者（COC-ID19陽性者）数の推移（１週間当たり）は
図１～図３の様に推移しており、黒色点線は移動平均による平滑化である。
これによると、その周期は112日～182日であり、現在（11月１１日時点）において、第8波に差し掛かっているように見受けられる。この周期は東京都民の免疫獲得に要する期間だと考えられないこともないが、予防対策など色々な要因が関与していると思われる。
図３を見ると、現在は第８波の入り口に差し掛かっているようであり、もし、この予測どおり推移すれば、第8波のピークは来年の3月頃だと推測される。
（データは「都道府県データランキング」より引用し編集した）
図１ 2020年の感染者数（１週間当たり）推移
図２ 2021年の感染者数（１週間当たり）推移 
図３ 2022年の感染者数（１週間当たり）推移
統計技術：第8章 要約統計量による効果量の計算(続き)
第8章-2：要約統計量（Summary）による効果量(続き)
前回に引き続き、
下記URLのUCCS（Free Online Calcultoer）を使って効果量（ES：Effect Size）を求める方法の紹介です。
https://www.psychometrica.de/effect_size.html
上記URLから、下記を選択してみて下さい。
#4. Effect size estimates in repeated measures designs
ここでの反復測定 t 検定 は、簡単に言うと、繰り返しのあるANOVA検定を2標本に適用した場合と考えて良いでしょう。
すなわち、
2 つの観測値にわたる時間または被験者内の連続結果の変化を相関関係を考慮して評価するために使用されています。
そのため、
これまでに紹介した「独立標本の t 検定」や「対応のあるｔ検定」とは異なります。
簡単な例題でやってみましょう。
図１ 対応のある t 検定の例題（仮定）を使用
Summary data( mean, sd)を使います。
上記UCCSの「#4」を開きます。
図２ Summary data の入力と結果 
Correlation= 0.5 の場合、
d_RM= 0.448 ( Cohen's effect size for repeated measures )
d_RM, pooled= 0.409
↓
この値は、次式と一致します。
S_diff= SQRT(sd1^2 + sd2^2 - 2 * r * sd1 * sd2)= 0.409
d_av= 0.413 (Cohen's d using an average variance )
↓
この値は、次式と一致します。
d_av= mean_diff／( ( sd1+ sd2 )/2)= 0.413
なお、
対応のあるt-test ( paired t- test ) の場合、その ES は、
Cohen’s d= (16.4 - 0 )／9.49 = 1.7281
・・となり、
反復測定 t 検定（repeated measures t-test）のESとは異なります。
すなわち、
反復測定は、同じ測定が時間の経過とともに繰り返されるペア データのサブタイプであり、複数のレベルで同じ被験者を使用するか、類似の特性または関係に基づいて各グループで参加者をペアにするかなど、介入試験の計画によって使い分けされます。
文責：ISL assistant staff KUMI
次回に続く！
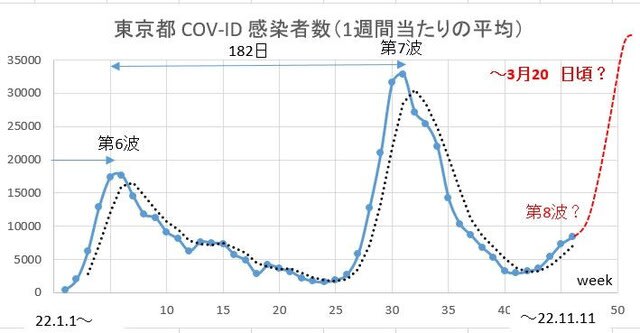
第Ⅲ部：第8章 要約統計量（Summary）による効果量の計算
ここでは、”Free Online Calculator”を利用し、”summary data”から効果量（ES：Effect Size）を求める方法を紹介しています。最近の学術誌などでは、要約統計量にESの記載が多く見られるようになり、また、査読者からESの記載を求められることが多くなってきています。そこで、
知りえた要約統計量からESを求める方法を具体的な例題でやってみたいと思います。
既に、
「第Ⅲ部：第６章-1 独立２標本の ｔ-検定の方法」では、下記の”Free Online Calculator”でその方法を紹介しています。
***
# 「Psychometrica の事例」
https://www.psychometrica.de/effect_size.html
このサイトでは、２群間の ｔ検定によるESの計算を下記により計算します、
・ サンプルサイズが同じとき（Cohen’s d and Glass Δ）→[1] を選択
・ サンプルサイズが異なるとき （Cohen's d, Hedges' g）→[2] を選択
上記[１] の場合（2 つのグループの n が同じである場合）；
そのＥＳは、「Cohenのd」 と呼ばれ、共通の標準偏差に関するグループ間の差を表します。
上記[2] の場合（2 つのグループの n が異なる場合）；
サンプルサイズの重みで調整することにより、標準偏差の正のバイアスを修正した「Cohenのd」 と全体的に同じで、修正された測定値であることを示しています。
上記[1][2]での、CLES(McGraw & Wong, 1992) はノンパラメトリックな効果サイズです。
第8章-1：要約統計量（Summary）による効果量（１）
この章では、下記の"Free Online Calculator"を紹介しますので、下記サイトにアクセスして下さい。
# 「Psychometrica の事例」
https://www.psychometrica.de/effect_size.html
上記サイトから、下記の「３」を選択して下さい。
# 3. Effect size for mean differences of groups with unequal sample size within a pre-post-control
上記[3]の場合、実験グループと対照グループの平均差のＥＳを求めます。
例えば、介入研究で、2 つのグループ (例えば、実験グループと対照グループ) を比較するときなどに提案されている方法です（retest-postest-Control design）。
この様な場合、両方のグループの効果サイズを計算することが考えられますが、”Carlson & Smith, 1999”によると、Pre-Postの平均の差を重み付けすることを主張しています。
次の簡単な例題で試してみましょう。
図１ PreTest - PosTest Data
本例でのsample size は同じですが、異なるときは自動的に修正されます。
図２ 入力と出力の画面
ESは、Morris (2008)=2.002 と Klauer(2001)=2.661 と出力され、共にHedge の g の差を表します。
ここで、単純な統計的検定として、２つのグループの前後差（diff.=Post-Pre）に注目するなら、図３のようになります。
図３ ２つの前後差（diff.=Post-Pre）の比較
すなわち、効果量 ES_d=2.697 となります。
一方、
２つの前後差（diff.=Post-Pre）を独立２群のｔ検定を行うと次のようになりました。
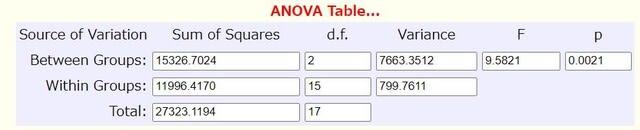
図４ 独立２群のｔ検定（前後差 diff.=Post-Pre）の結果
２群の「diff」（図１）から、その独立2群のｔ検定の結果は次の通りでした。
...diff......Treat Group......Control
..mean..........65...............-3.8
...sd............22.5.............28.2
....n...............5.................5
df=8
t value=4.2493
p value=0.0028
よって、effect r は次式のより求めることができます。
√t^2/t^2+df ＝0.8324
この計算を、”Free Online Calculator”で確かめたいなら、下記Web site を試してみて下さい。
UCCS：
https://lbecker.uccs.edu/
このサイトでは、下記の要約統計量で計算できます。
(1) means and standard deviations
(2) independent groups t test values and df
図５ 上記（１）の場合
図６ 上記（２）の場合
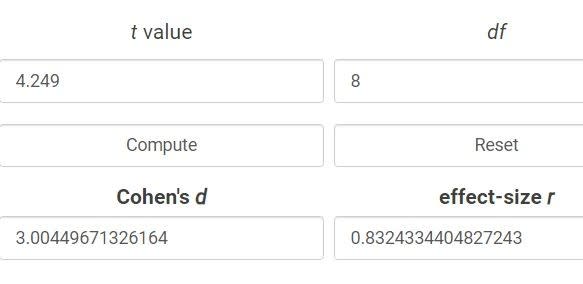
要約統計量の丸めにより多少の違いがあります。
その他として、次のようなsite があります。
# Practical Meta-Analysis Effect Size Calculator
https://www.campbellcollaboration.org/escalc/html/EffectSizeCalculator-R3.php
# Effect size converter
https://www.escal.site/
次回に続く！
文責：ISL assistant staff, KUMI
第Ⅲ部 Free Online Caluclator （例題集）
第7章 要約統計量（Summary）によるANOVA検定
３標本以上の平均値差の検定には、通常、一元配置分散分析で全体での有意差について知ることが出来ます。
有意な差があると判断されたら、どの標本間に有意差があるかを調べる必要が出てきます。これらの事につては既に、
下記のGooブログ：「第８章 多標本の平均値差の検定」で紹介しています。
https://blog.goo.ne.jp/k-stat/e/79168d9e0b668b178e025f72a9ae5b8f
http://toukei.sblo.jp/article/187495709.html?1589594310
ここでは、
”summary data” による”Free Online Calculator”での方法を紹介する訳ですが、その理由は次の様なものです。
１. The gereric method for any statistical technique used to analyze from summary data .
つまり、
要約データ（統計量）からの統計手法の一般的な方法の紹介です。
2. The intention of statistical testing technique is to attempt to predict the quality of the "Free Online Software (Calculator) product.
つまり、
その意図は、「無料オンライン ソフトウェア (電卓)」製品の保証です。
そして、
信頼できる"Free Online Calculator"によって、統計分析が身近になり、繰り返し検討出来るようになれば、なんとなく敬遠しがちな統計分析も、ごく普通の演算のように気軽に使える様になるかもしれません。
また、
要約統計量は、手元にあるデータを理解したり、データ に関する情報を伝達したりするのに役立つと共に、その後の統計分析にも役立ちます。
よろしければ、ISLの”久美”と一緒に簡単な例題を試してみましょう。
例題は下記URLの「血中コレステロール改善剤」の"Summary data" を用いてみましょう。ただし、”対応のない”ものとして実行します。
使用する”Calculator”は下記の通りです。
# StatPages.net website
● https://statpages.info/anova1sm.html
図１ summary data の入力画面
図２ 出力結果
ANOVA table（p<0.05）から全体の平均値には有意差があると判断されます。よって、どの組合せに有意な差があるかを「Post-hoc-test」で調べることになります。ここでの多重比較は「Tukey HSD ("Honestly Significant Difference")」となります。
図３ ”Post-hoc-test”の結果
”Tukey HSD test」から、有意差のある組み合わせは、次に通りでした。
● Group 1 vs Group 3: p=0.0016
● Group 2 vs Group 3: p=0.0385
最近の一元配置では、実験計画の要因効果よりも多重比較に注目する場合が多く、ANOVAを省略し、いきなり多重比較を行う事例が見受けられます。これは統計ソフトの普及と関連しているようです。
”Post-hoc-test”が必要ない場合は、下記のサイトも利用出来ます。
● https://home.ubalt.edu/ntsbarsh/Business-stat/otherapplets/SeveralMeans.htm
図４ summary data の入力画面
Sample Variance はSD^2 で良いでしょう。
図５ 出力結果
注釈：対応のない一元配置分散分析として実行しました。
今回の投稿から、ISLの”久美”(アシスタント・スタッフ)が担当致しますので、どうぞよろしくお願い致します。
第Ⅲ部 Free Online Caluclator （例題集）
第６章-2：対応する２標本のｔ-検定の方法
前章前項は独立２標本のｔ検定をsummary data を用いて検定する方法であり、統計技術的に"Free Online Calculator"を用いた簡単・容易な技術を紹介しました．
ここでは、
対応する２標本を手軽におこなえる方法を紹介しましょう．
この方法については、本稿「統計技術」で既に紹介していますが、"summary data" を用いて方法を簡単な例題でやってみたいと思います．
例題は、Gooブログ：統計技術 第Ⅰ部「第7章-5 対応する２標本の差の検定について」です．
http://toukei.sblo.jp/article/187434857.html
Summary data は次の通りです．
.......................夫のスコアー.....妻のスコアー
データ数(n)...........10
平均値(mean)........182.4...............147.6
標準偏差(sd).........14.57................13.69
使用する「Free Online Calculator」（下記Web サイトの場合）
# Statistics Kingdom
https://www.statskingdom.com/paired-t-test-calculator.html
実行
図１ sammary data の入力画面
Average(Xd:)は差の平均値(34.8)、Sample SD(sd:)は差の標準偏差(20.093)です．
↓
[ Calculate ]
図２ 出力結果
1. H0 hypothesis
Since the p-value < α, H0 is rejected.
The Before population's average is considered to be not equal to the After population's average.
In other words, the difference between the averages of Before and After is big enough to be statistically significant.
つまり、
1.H0仮説
p 値 < α であるためH0 は棄却され、前後の母集団の平均差は、等しくない、すなわち、前後で有意な差があると見なされる．前後 の平均値の差は、統計的に十分に有意であると言える．
2. P-value
The p-value equals 0.0003917, ( P(x≤5.4769) = 0.9998 ).
It means that the chance of type I error (rejecting a correct H0) is small: 0.0003917 (0.039%). The smaller the p-value the more it supports H1.
つまり、
p 値=0.0003917 で、タイプ I エラー (正しい H0 を拒否する) の可能性が小さいことを意味しており、p 値が小さいほど、H1 を支持してしている．
3. Test statistic
The test statistic T equals 5.4769, which is not in the 95% region of acceptance: [-2.2622, 2.2622].
The 95% confidence interval of After minus Before is: [20.4263, 49.1737].
つまり、
検定統計量 T=5.4769 で、95% の許容範囲 [-2.2622, 2.2622] にはなく、前後の 95% 信頼区間は [20.4263, 49.1737] である．
4. Effect size
The observed effect size d is large, 1.73.
This indicates that the magnitude of the difference between the average of the differences and the expected average of the differences is large.
つまり、
観測された効果量 d =1.73 で、前後差の平均が大きいことを示している．
もし、
携帯（スマートフォーン）なら、下記の「KASIO」サイトが便利かも知れません．
# KASIO
https://keisan.casio.jp/exec/user/1490619220#!
図３ CASIO の入力と出力画面
データの入力；
標本平均[34.8]、標本分散分析[403.73]（sd^2）、サンプルサイズ[10]
***
別の"Free Online Calculator"として、下記Webサイトを紹介しておきましょう．
# EPITOOLS (One-sample t-test on summary data)
https://epitools.ausvet.com.au/onesamplettest
summary data の入力は図１と同じ様にすれば良いでしょう．
***
文責：ISL asistant staff 久美
