こんにちは・・、情報統計研究所（ISL）の”久美”です。
私は”ISL”のアシスタントとして統計分析に必要な技術を学んでいるところです。
そして、統計分析で必要なことは”統計へのセンス”ではないかと思うようになりました。
”センス”は色々な経験から身につくものかも知れませんね！
現在、
Gooブログに投稿中の”統計技術”が少しでも皆様の”センス”に役立てば幸いです。
今後とも”ILS”をよろしくお願いします。
次回の統計技術は、
「第Ⅲ部 Free Online Caluclator （例題集）、第６章-2：対応する２標本のｔ-検定の方法」の予定です。
第Ⅲ部 Free Online Caluclator （例題集）
統計技術 第Ⅲ部 第６章-1(2)：独立２標本の ｔ-検定の方法（続き）
同章前項では、t 検定と Effect size を別々の"Free Online Calculator"で求めたが、ここでは ｔ検定と ESの結果を同時に見ることが出来るサイトを紹介しておこう．
下記のサイトにアクセスして、同章前項で用いた例題を試してみよう．
# Statistics Kingdom
https://www.statskingdom.com/140MeanT2eq.html
図１ Summary data の入力画面
↓
[ Calculate test ]
図２ 出力結果の画面
ここで、
1. H0 hypothesis
Since p-value < α, H0 is rejected.
The average of Group-1's population is considered to be not equal to the average of Group-2's population.
In other words, the difference between the sample average of Group-1 and Group-2 is big enough to be statistically significant.
つまり、
統計的にｐ値は有意（p<0.05）であり、2つの標本の母集団の平均値は等しくないと見なされ、その差は統計的に十分に大きいと判断される．
2. P-value
The p-value equals 0.005255, ( p(x≤T) = 0.002627 ). It means that the chance of type I error (rejecting a correct H0) is small: 0.005255 (0.53%). The smaller the p-value the more it supports H1.
つまり、
p 値は 0.005255（両側） は、第1種の過誤（TypeⅠerror ) 、すなわち誤って帰無仮説を採択する可能性が小さいことを意味している．
3. The statistics
The test statistic T equals -2.9714, which is not in the 95% region of acceptance: [-2.0281 : 2.0281].
x1-x2=-3.27, is not in the 95% region of acceptance: [-2.2319 : 2.2319]. The standard deviation of the difference, S' equals 1.1, is used to calculate the statistic.
つまり、
検定統計量 T＝ -2.9714 は 95% 許容領域 [-2.0281 : 2.0281] にはなく、また、平均値の差（x1-x2=-3.27） も、95% の許容範囲 [-2.2319 : 2.2319]にない．
4. Effect size
The observed effect size d is large, 0.96. This indicates that the magnitude of the difference between the average and average is large.
つまり、
効果量 d＝0.96と大きく、平均と平均の差の大きさが大きいことを示している．
また、次のようなコメントが表記される．
Based on a two-tailed F test, σ1 is considered as unequal to σ2 (p-value is 0.00594)．
つまり、
両側 F 検定に基づいて、σ1 は σ2 と等しくない（不等分散）と見なされる (p 値は 0.00594)．
***
両側 F 検定（不等分散）に基づいて、必要なら下記で"Welch's T-test" を行えば良い．
# Two Sample T-Test Calculator (Welch's T-test)
https://www.statskingdom.com/150MeanT2uneq.html
統計技術 第Ⅲ部：第６章 要約統計量（Summary）による検定法
統計技術 第Ⅲ部では、Free Online Caluclator として「Wessa.net」紹介してきた．
統計事例によっては原（生）データ（Raw data）ではなく、要約統計量（データ数、平均値、標準偏差・・など）から平均値差の検定や効果量（effect size）などを知りたい場合がある．その様なときに役立つ" Free Online Caluclator "の事例を紹介しておこう．
第６章-1：独立２標本の ｔ-検定の方法（2-sample t-test for summary data）
例題として、下記URLの「統計技術：第Ⅰ部第７章」の統計量を用いてやってみよう．http://toukei.sblo.jp/article/187281663.html
Summary data は次の通りである．
--------------------------
.........................ｘ............y
平均値......10.65......13.92
分散.............4.69......18.32
標準偏差....2.166......4.28
データ数......19..........19
---------------------------
利用する「Free Online Caluclator」(URL)にアクセスしてみよう．
# EPITOOLS の事例
https://epitools.ausvet.com.au/twosamplettest
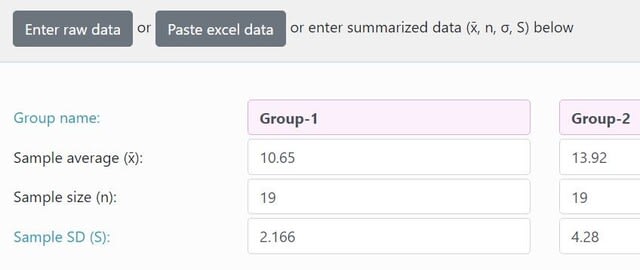
図１-1：Summary data の入力画面（１）
図１-2：Summary data の入力画面（２）
図２：Summary data の出力画面（Ｅｘｃｅｌへの出力を編集したもの）
「Download Excel file of result」をクリックすればよい．
図３：Summary data の95％ＣＩ グラフ
最近の学会発表や学術誌への投稿などでは、効果量（ES：effect size）の記載が求められることが多くなっている．ESについては、当該Gooブログで紹介しているが、代表的な" ES Caluclator "を紹介しておこう．
# Psychometrica の事例
https://www.psychometrica.de/effect_size.html
Top ページ
↓
Effect Size
↓
1. Comparison of groups with equal size
[+]をクリック
↓
図５ 入力と出力画面
ここで、
Effect Size d_Cohen ＝ 0.964 である.
これは、次式によって求められる（サンプル数が同じとき）．
d=(mean_1 - mean_2)／sample SD pooled
sample SD pooled=sqrt((SD1^2 + SD^2)／2)
従って、
d=abs(10.65-13.92)/sqrt((2.199^2 + 4.28^2)/2)=3.27/3.392=0.964
となる．
サンプル数が異なるときは、sample SD pooled の計算が異なるので、次の例題を試してみょう．
統計のコツのこつ(31)
https://blog.goo.ne.jp/k-stat/e/3ce0391051242c38d99a3a925be39d22
----------------------------------------------------------------------
(A) 年齢 30～39才, 30名の平均値 Ｘa＝122.5 mmHg, 標準偏差 SDa＝ 10.85 mmHg
(B) 年齢 40～49才, 20名の平均値 Ｘb＝133.4 mmHg, 標準偏差 SDb＝ 12.24 mmHg
----------------------------------------------------------------------
# Psychometrica の事例
Top ページから次の項目を選択する．
2. Comparison of grouos with different sample size (Cohen's d, Hedges'g)
↓
図６ Summary data の入力と出力結果の画面
ここでの、
Effect size = 0.954 は"Hedges's g" の値と一致する．
これは、次式によって求められる（サンプル数が異なるとき）．
g=(mean_1 - mean_2)／sample SD pooled
sample SD pooled=((n1-1)*SD1^2 + (n2-1)*SD^2)／(n1+n2-2)
従って、
g=10.9/11.4247=0.954073
となる．
また、
図６ の[*][**]については欄外に注釈があり、大雑把に言うと次のようである．
-------------------------------------------------------------------------------
[* ]：これは単純に dCohen または gHedges と呼ばれ、修正された測定値であることを示す．
[**]：あるグループのサンプルが別のグループのサンプルよりも大きい確率である.
-------------------------------------------------------------------------------
通常なら、Effect Sizeとして「Cohen's d 」を採用すれば良いだろう．
しかし、
Hedges'g は"unbiased Cohen's d" と呼ばれるように、求める計算式が違っており、今だ混乱しているので、「Cohen's d 」か「Hedges’g」を明確しておくことをお勧めする．
統計技術 第Ⅲ部 Free Online Caluclator （例題集）
第5章-2：2-way ANOVA
二元配置分散分析（2-way ANOVA）は、すでに、第Ⅰ部：「第11章-2 ２元配置分散分析(繰返しあり)」（下記URL）で紹介している．
https://blog.goo.ne.jp/k-stat/e/81cb98056a300b37bba3727efbfe7a3f
ここでは、上記URLを参考に「Free Online Caluclator」（Wassa）で「R」を気軽に使ってみよう．
Wessa.net のTop ページ
http://wessa.net/
↓
Statistica Hypothesis Testing Software
↓
Bivariate and Multivariate Statistical Hypothesis Testing
- Ungrouped Data
↓
2-way ANOVA
グループ間のANOVAを計算する．
↓
Data X を確認
↓
Names of X columns を確認
↓
Response：Variable 1 を確認
↓
Factor：Variable 2 を確認
Factor：Variable 3 を確認
↓
Compute
出力結果：
図1 ANOVA table
図２ Tukey Honest の対比較検定の結果
図３ グループごとのBoxPlot
図３ グループ間の相互作用のグラフ
2つの直線（FとM）の伸びは異なっており、交互作用がグラフから確認できる．
それでは、
第Ⅰ部：「第11章-2 ２元配置分散分析(繰返しあり)」での例題でやってみよう．
図４ 「R」のためのデータフォーム
このデータのfactor(A, B)に「” ”」を付けて、Data Xに入力するか、事前にExcel で作成したものをコピー＆ペーストすればよい．
その分析結果（出力）は図５のとおりである．
図５-1 入力データ（図４）の出力結果(1)：ANOVA model 係数
この例題でのANOVA modelでは・・、
「Resoponce~ Treatment_A * Treatment_B」となっているが、実際には「Value~ factor_A * factor_B」から求めた係数であり、2 つの予測変数間の [*] は交互作用効果もテストすることを示している．
この例では、
応答変数として「Value」 を使用し、2 つの予測変数として「factor_A と factor_B」を使用して、 ANOVA モデルを適合させている．
なお、
このANOVA model から、次により各グループ間の平均値を求めることができる．
図5-2 ANOVA model から求めた各グループ間の平均値
図6 入力データ（図４）の出力結果(2)：ANOVA table
２元配置分散分析表であり、「Treatment→facter」である．
図7 入力データ（図４）の出力結果(3)：Tukey Honest の多重比較
多重比較の結果を示している．
図8 入力データ（図４）の出力結果(4)：グループ間の相互作用のグラフ
この図から、交互作用のあることが視覚的に確認できる（図６のTreatment_A：Treatment_Bのｐ値＝0.004 で有意である）．
さらに、
「R」での”Box Plot の描き方”と”グループ間（A、B）の平均値”を紹介しておこう．
「R」コマンド：
----------------------------------------------
ibrary(dplyr) # 事前にインストールしておく
library(ggplot2) # 事前にインストールしておく
# Box Plot の描写
ggplot(data = dat, aes(x = A, y = Value, colour = B)) +
geom_boxplot()
# グループ間の平均値
group_by(dat, A, B) %>%
summarise(mean=mean(Value))
----------------------------------------------
出力結果：
図10 グループ間のBox Plot
図11 グループ間の平均値
統計技術 第Ⅲ部 Free Online Caluclator （例題集）
第5章：1-way ANOVA
一元配置分散分析（1-way ANOVA）は、すでに第Ⅰ部：第9章-2 ３群における"One way ANOVA" で紹介している（下記URL）．
http://toukei.sblo.jp/article/187608681.html
上記URLを参考に、ここでは「Free Online Caluclator」で「R」を気軽に使ってみよう．
ここでの"1-way ANOVA" calculator は、一元配置分散分析 表(ANOVA tacle) を迅速かつ簡単に作成するのに役立ち、これには、平方和、平均平方、自由度、F 値、P 値など、観測データ セットからのすべての関連情報が出力される．
それでは、やってみよう．
Wessa.net のTop ページ、
http://wessa.net/
↓
Statistica Hypothesis Testing Software
↓
Bivariate and Multivariate Statistical Hypothesis
Testing- Ungrouped Data
↓
1-way ANOVA
↓
グループ間のANOVAを計算する．
↓
Data X を確認
↓
Names of Treatment を確認
↓
Response Variable と Facter Variable を確認
↓
Compute
↓
図１ 出力結果(1)：分散分析表
図2 出力結果(2)：多重比較
「Tukey Honest」とは のテューキーのHSD (honestly significant difference) の多重比較のことである．
図3 出力結果(3)：等分散性の検定
等分散性の検定(Levens Test)の結果が出力される．
それでは、別のSampe の事例「第Ⅰ部：第9章-2 ３群における"One way ANOVA"」で使用したデータを使ってやってみよう・・、結果は図４の通りである．
図４ 「第Ⅰ部：第9章-2」の原データ
上記データを図５のように入力する．
図５ 図４のデータの入力様式
「R」のaov() を使用しているので、結果は当然、Free Online Calculator(Wessa.net)と一致する．
