前回に続き効果量と検出力について考えて見ましょう。
母平均の差の検定には、常に、2つの過誤(α-error と β-error)が付きものです。
図:2つの過誤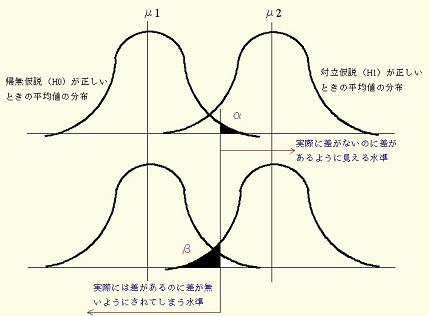
検出力は、検出力=1-β であり、本当に差がある場合に正しく検出できる確率です。
参照先(やさしい医学統計手法「3.1.3」)
URL:
http://kstat.sakura.ne.jp/medical/med_001.htm
前回の例題における標本検出力は、検出力=f(Na , Nb , e.s. , α)から、適切な検出力があったか、どうかを知る事が出来ます。適切な検出力かどうかは、
「A Power Primer by Tacob. Cohen ( 1992 )」の「Table1; ES Indexes and Their values of Small , Medium and Large Effects」を参考にして下さい。t-test での e.s. のは、
Small=0.20 , Medium=0.50 , Large=0.80
となっていますので、0.80を目安にすれば良いと思います。前回の例題から、
有意差のあったA年代間の有意水準(α=0.05)の検出力は次の通りです。
t-value(p-value) e.s. power
A年代とB年代 3.297(0.0018) 0.952 0.898
A年代とC年代 2.445(0.0325) 0.893 0.664
ここで、A年代とC年代間のPower を上げるには、C年代のデータ数(N)を増やす必要が有りそうです。C年代のデータ数を N=21 にしたとき、
Welth t-value=3.278、p=0.002 となり、e.s.=0.933、Power=0.895
となりました。この様に、2つの平均値の差の検定結果に、e.s. と Power を併記するようになれば、検定結果の信頼性を高めるかも知れません。









