統計技術 第Ⅲ部:第2章 多変量記述統計
第2章 Bivariate Descriptive Statistics (二変量記述統計)
Wessa.net 事例集から、2つ以上の変量からなるデータの統計量記述に関する技術を紹介する.
多変量、すなわち2つ以上ののグループ化されていない独立した2つ以上の標本の生データの統計量であり、2つ以上の相関関係や代表値の有意差検定など多岐の分析となる.
なお、例題は、そのまま利用するので、実際の分析に当たってはサイトの使用方法に従って実行されたい.
● Free Statistics Software (Calculator) - Web-enabled scientific services & applications
https://www.wessa.net
第2章-1 Bivariate Descriptive Statistics (二変量統計記述)
二変量記述統計では、2つの標本の変数を分析・比較して、変数間に関係を要約する.
「Wessa.net」のTop ページから、
Descritive Statistisc を選択
↓
下方にスクロースして、
図1 「Bivariate Descriptive Statistics」のデータ入力画面
↓
● Correrationを選択
↓
図1 データ入力画面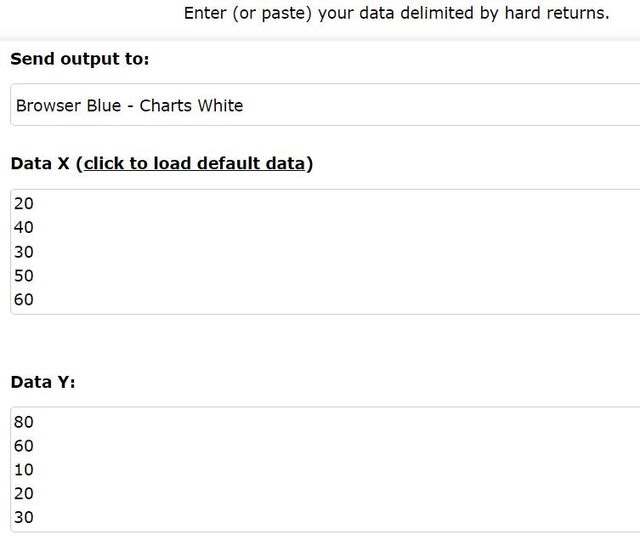
↓
「Compute」をクリック
図3 出力結果(1)
ここで、
.統計量とExcel 関数は次の通りである.
------------------------------------------------------------------------------
Mean:平均値.....=AVERAGE()
Biased Variance:母集団分散.....=VAR.P()
Biased Srandard Deviation:母集団標準誤差.....=STDEV.P()
Covariance:標本共分散.....=VAR.S()
Correlation:相関係数(r).....=CORREL()
Determination:決定係数(R^2).....=r^2
T-Test:相関係数のt検定....Excel の「データ分析→回帰分析」
p-value(2 sided):相関係数のt検定の両側p値....上記から
p-value(1 sided):相関係数のt検定の片側p値
95% CI of Correlation:母相関係数の95%CI...下記参照
Degree of Freedom:自由度....N-2=5-2=3
Number of Observations:データ数....N=5
-------------------------------------------------------------------------------
「95% CI of Correlation」計算の参照先URL:
情報統計研究所(やさしい医学統計手法)
↓
「6.3. 相関と回帰について」を参考にExcel で計算できる.
図3 出力結果(2):Normality Test(正規性の検定)
Bivariate-4.jpg
ここで、
・jarque-Bera Normality Test(ジャック-ベラ検定)
data: X
JB=0.35208 (p=0.8386、片側検定)
data: Y
JB=0.54552 (p=0.7613、片側検定)
正規分布に従うSkewness(歪度)かKurtosis(尖度 )かを調べるもので、p値から正規分布と判断される.
なお、
小標本の場合には有意に傾きやすいので、p値の補正が必要との説もある.
次回に続く!









