分析依頼が立て込むと投稿が途切れてしまいました。バタバタしていましたが、今回も色々な統計学的検定での効果量についてご紹介したいと思います。それでは、
「すぐに役立つ統計のコツ」(第4章:29ページ)の一元配置分散分析での効果量です。
第4章の冒頭は、多重比較の方法を紹介しています。これは、どの組み合わせに有意差があるかに重点をおいたものです。
***
注釈:
「ホルム・ボンフェローニやチューキのHSD」はF値を用いないので、分散分析と切り離しても良いと考えています
***
注釈:
「ホルム・ボンフェローニやチューキのHSD」はF値を用いないので、分散分析と切り離しても良いと考えています
***
一元配置分散分析については、本書(35ぺージ)に紹介しています。ここでの例題(表4.3)で分散分析にける効果量を求めて見ましょう。但し、
今回は無料のソフトでやって見たいと思います。
今回は無料のソフトでやって見たいと思います。
効果量を求める色々な無料ソフト(webオンラインソフトなど)がありますが、ここでは、その中でも、名の知れた検出力分析ソフト「G・Power」をご紹介しましょう。
まずは、
下記URLにアクセスして下さい。
下記URLにアクセスして下さい。
http://www.gpower.hhu.de/
上記から、圧縮ファイル(GPowerWin_3.1.9.2.zip)をダウンロードします(2017年3月現在)。
warranty whatsoever.
Download G*Power 3.1.9.2 for Windows XP, Vista, 7, 8, and 10 (about 20 MB). Please make sure to choose “unpack with folders” in your unzip tool.
Download G*Power 3.1.9.2 for Windows XP, Vista, 7, 8, and 10 (about 20 MB). Please make sure to choose “unpack with folders” in your unzip tool.
圧縮ファイルを適当なフォルダーに解凍し、「setup.exe」を起動させインストールすれば、Window10の場合、通常、下記のホルダーに実行ファイルが作成されると思います。
ローカルディスク(c)→ProgramData→Microsoft→Windows→スタートメニュー→プログラム→GPower→GPower 3.1を実行
Windows10であれば、
アプリの「G」に「GPower」のアイコンが出来ていると思います。それでは、
アプリの「G」に「GPower」のアイコンが出来ていると思います。それでは、
「GPower3.1」をクリックして実行して見て下さい。
図1の様な画面が立ち上がったと思います。
図1 初期画面
そして、
図2の番号の手順で行えば良いでしょう。
図2の番号の手順で行えば良いでしょう。
図2 GPowerによる手順
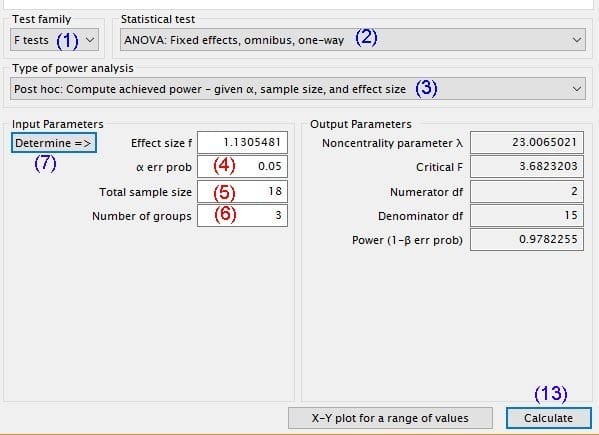
(1)F test→(2)ANOVA:Fixed effect, omnibus, one-way→(3)Post hoc:→(4)(5)(6)
「(4)はα=0.05、(5)(6)は「すぐに役立つ統計のコツ」34ページの表4.3から、全サンプル数=3×6=18と列数=3 を入力します」→(7)Determine をクリック→図3の画面へ
図3 効果量の計算

図3の画面で、
「Select procedure」をクリック→(8)「Effec size from variance」を選択→(9)(10)は「すぐに役立つ統計のコツ」36ページ(表4.8)の分散分析表から、
(9)=変動要因:グループ間の「15330」を、(10)=グループ内の「11994」を入力→
(11)Calculate をクリック→Effect size f が出力されます→
(12)Calculate and transfer to main window をクリックすれば図2に効果量が転送されますので、
最後に、
図2の(13)Calculate をクリックすれば、Output Parameters が出力されます。
図2の画面から、
効果量(Effect size f)=1.1305、検出力(Power)=0.9782(97.82%)
であることが分かります。
***
効果量の筆算:
効果量の筆算:
「すぐに役立つ統計のコツ」36ページ(表4.8)の分散分析表から、
f <- sqrt( SSa / SSe ) =√(グループ間の変動/グループ内の変動)=√(15330/11994)=1.131
となります。ここで、
寄与率(ρ):全変動の何%が変動要因(SSa)によって説明されるかの指標は、
ρ=SSa / SSt=グループ間の変動/全体の変動=15330/27324=0.561(56.1%)
となりますが、純変動を用いた寄与率(ρ´)は、
ρ´=(SSa-df_a×Ve )/ SSt=(グループ間の変動-自由度_a×グループ内分散)/全体の変動=(15330-2×799.6)/27324=0.503
ρ=SSa / SSt=グループ間の変動/全体の変動=15330/27324=0.561(56.1%)
となりますが、純変動を用いた寄与率(ρ´)は、
ρ´=(SSa-df_a×Ve )/ SSt=(グループ間の変動-自由度_a×グループ内分散)/全体の変動=(15330-2×799.6)/27324=0.503
で求めることができます。
ここで、
グループ内分散とは、誤差分散のことです(すぐに役立つ統計のコツ:36ページ参照)。
また、
純変動とは変動から自由度に比例した分の誤差分散を引いたものだということです。
グループ内分散とは、誤差分散のことです(すぐに役立つ統計のコツ:36ページ参照)。
また、
純変動とは変動から自由度に比例した分の誤差分散を引いたものだということです。
なお、
η^2(イータの2乗)=SSa/SSt=0.561
η^2(イータの2乗)=SSa/SSt=0.561
であり、寄与率(ρ)と同じです。
商用統計ソフトによって、計算方法の違いから多少の違いがありますのでご注意下さい。
詳しくは、
下記のwebサイトをご参考になさって下さい。
統計学入門 第4章(杉本典夫先生)
http://www.snap-tck.com/room04/c01/stat/stat04/stat0401.html
http://www.snap-tck.com/room04/c01/stat/stat04/stat0401.html
次回に続きます。
情報統計研究所はここから!


















