統計のコツのこつ(31)

 

このブログは「すぐに役立つ統計のコツ」(オーム社）に紹介されている内容に沿って書いています。
本書をお読みいただければ分かり易いかと思います。

今回は前回と同じように、
２つの標本の大きさ(n1,n2)、平均値(m1,m2)、標準偏差(s1,s2)だけが分かっている場合の"独立２群の平均値の差"の検定をやって見ましょう。

● 本書の第３章（10ページ）を参考にして下さい。

例題は、
「やさしい医学統計手法」(情報統計研究所：下記URL)から引用します。

URL:

http://kstat.sakura.ne.jp/medical/med_014.htm

 

例題は次の様になっています。

(A)年齢 30～39才, 30名の平均値 Ｘa＝122.5 mmHg, 標準偏差 SDa＝ 10.85 mmHg
(B)年齢 40～49才, 20名の平均値 Ｘb＝133.4 mmHg, 標準偏差 SDb＝ 12.24 mmHg
(C)年齢 50才～～, 10名の平均値 Ｘc＝139.0 mmHg, 標準偏差 SDc＝ 20.40 mmHg

 

筆算の過程は「やさしい医学統計手法」を見て下さい。

ここでは、
Excelの関数を使った方法のご紹介です。

図１の様なフォーマットを作ります。

 

図１　ｔ検定のためのフォーム

 

 

そして、以下の関数式を各セルに入力しておいて下さい。

 

・平均値の差 Ｃ列５行(1)：=C2-C3
・95%CI_Lower Ｄ列５行(2):=ROUND(C5-T.INV.2T(0.05,B2+B3-2)*E10,3)
・95%CI_Upper Ｅ列５行(3)：=ROUND(C5+T.INV.2T(0.05,B2+B3-2)*E10,3)
・自由度　
　Ａ群 Ｃ列７行(4)：=B2-1
　Ｂ群 Ｄ列７行(5)：=B3-1
  全体 Ｅ列７行(6)：=B2+B3-2
・併合した分散
　Ａ群 Ｃ列８行(7)：=D2^2*(B2-1)
　Ｂ群 Ｄ列８行(8)：=D3^2*(B3-1)
　全体 Ｅ列８行(9)：=(C8+D8)/E7
・併合した標準偏差 Ｅ列９行(10)：=SQRT(E8)
・平均値差の標準誤差 Ｅ列10行(11)：=E9*SQRT(1/B2+1/B3)
・ｔ値 Ｅ列11行(12)：=C5/E10
・ｐ値 Ｅ列12行(13)：=T.DIST.2T(ABS(E11),E7)
・標本効果量 Ｃ列13行(14)：=ROUND(ABS(E11*SQRT((B2+B3)/(B2*B3))),5)
　S_e.s. Ｅ列13行(15)：=SQRT((B2+B3)/(B2*B3)+C13^2/(2*E7))
・e.s. 95%CI Ｃ列14行(16)：=ROUND(C13-1.96*E13,3)
　e.s. 95%CI Ｄ列14行(17)：=ROUND(C13+1.96*E13,3)

 

ここで、
例数(n)、平均値(m)、標準偏差(sd)を入力すれば、次の結果(Student's t-test)が出力されます。

 

・平均値の差の95% 信頼区間
・ｔ値
・ｐ値
・効果量(e.s.)
・効果量の95％信頼区間

 

それでは、黄色のセルに例題(A)の数値を入力して下さい。

 

検定結果は、
図２で示した緑色セルに次のように出力されます。

 

図２　独立２群(対応のない)ｔ検定の結果

 

 

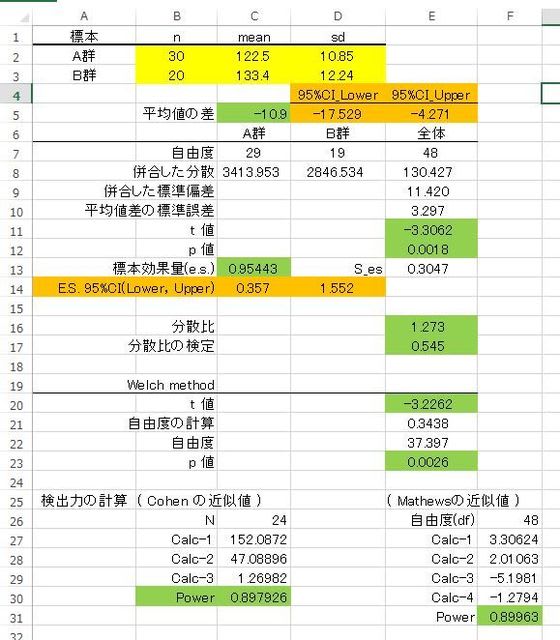
・平均値の差＝-10.9（95% CI＝-17.529～-4.271）
・ｔ値＝-3.3062（ｐ値＝0.0018）
・効果量(e.s.)＝0.954（e.s.の95％CI＝0.357～1.552）

なお、
分散比、及び、その検定と Welch method による t 値、自由度、p 値 は 図３の関数式で求められます。

 

図３ Welch method による関数式

　

 

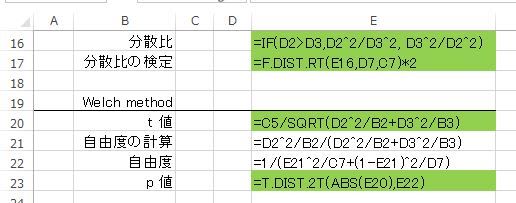
この例題での分散比は 1.273(ｐ＝0.545)で等分散と見なされます。

もし、
等分散でなければ「Welch method」の結果の採用を検討します。

詳しくは、
「すぐに役立つ統計のコツ」(18ページ)を見て下さい。

 

また、
検出力は図４、図５の関数式で近似値を求めることが出来ます。

 

図４　Cohen による近似値を求める関数式

 

 

図５　Mathews による近似値を求める関数式

 

 

・検出力（1-β）：
    Cohen近似値＝0.897926(89.8%)、Mathews近似値＝0.89963(89.9%)

 

・「R」による正確な近似値＝0.8993719（89.9％）

 

「R」による正確な検出力は次により実行して下さい。
---------------------------------------------------
library(pwr)
pwr.t2n.test(n1=30, n2=20, d=0.95, sig.level=0.05)

出力結果  
t test power calculation            
n1 = 30             
n2 = 20              
d = 0.954      
sig.level = 0.05          
power = 0.8993719    
alternative = two.sided
---------------------------------------------------

最近の論文等の記述では、効果量の併記が多く見られます。

情報統計研究所はここから！