統計のコツのこつ(52)

先のブログ「統計のコツのこつ(48)(49)」では、過去のCPK活性値のデータの一部を抜き出して、色々な回帰分析をご紹介しました。
別に、CPK活性値の統計学的な検討を目的とした訳ではなかったのですが、杉本典夫先生から級内相関(ICC)に関するご教示を頂きました。

ICCについては、杉本典夫先生の下記HPを見て下さい。

統計学入門-第5章(5.4 級内相関係数と一致係数)
http://www.snap-tck.com/room04/c01/stat/stat05/stat0504.html

 

ICCについて、解りにくいと思われた Viewers のためになるかどうか分かりませんが・・、ここでは、
ExcelでICCを筆算してみましょう。

 

例題は先の血清CPK活性値(図1)を用いてやってみます。

 

図１　血清CPK活性値(A1h：室温放置１時間、B1h：冷所保管１時間)

 

Excelでの方法：
Excel→データ→データ分析→分析ツール[分散分析：繰り返しのない二元配置]→
：入力範囲[$A$1：$C$21]、☑ラベル、α[0.05]、◎出力先｢任意に決める｣：→OK

 

この結果は、図２の分散分析表のようになります。

 

図２　血清CPK活性値(A1h：B1h)の二元配置分散分析表

 

 

 

図２の黄色セル部分(Within)は、次により計算で求めたもので出力されません。

Withuin[変動：=F4+F5、自由度：=G4+G5、分散：=F6/G6]

 

図２の各分散の値を用いてICC(図３)を求めます。

図３　各ICCの計算結果

 

 

 

図３の関数式は次の通りです。

 

 

 

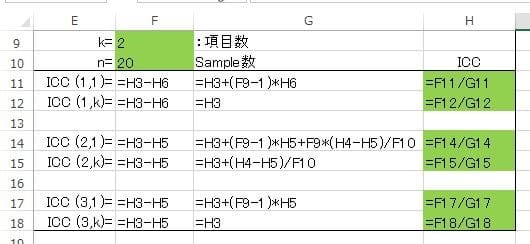
以上の様に、
ICCにはCase1、Case2、Case3 の3種類があり、

・検者内信頼性：ICC(1,1)やICC(1,k)............一元配置変量モデル
・検者間信頼性：ICC(2,1)やICC(2,k)、絶対一致..二元配置変量モデル
・検者間信頼性：ICC(3,1)やICC(3,k)、相対一致..二元配置混合モデル

 

での信頼性の指標と言えるでしょう。

もし、
SPSSの環境があるなら、次により３つのICCの関係が良く分かるかも知れません。

・SPSS→分析→信頼性分析→OK→項目選択［A1h, B1h］→統計［☑級内相関]、モデル[一元配置変量]→続行→OK
　[Single Measure Intraclass Correration = 0.9151]、[Average  Measure Intraclass Correration = 0.9557]

・SPSS→分析→信頼性分析→OK→項目選択［A1h, B1h］→統計［☑級内相関]、モデル[二元配置変量][絶対一致]→続行→OK
　[Single Measure Intraclass Correration = 0.9155]、[Average  Measure Intraclass Correration = 0.9559]
・SPSS→分析→信頼性分析→OK→項目選択［A1h, B1h］→統計［☑級内相関]、モデル[二元配置変量][一致性]→続行→OK
　[Single Measure Intraclass Correration = 0.9253]、[Average  Measure Intraclass Correration = 0.9612]

未熟な筆者ゆえ、やさしく悦明することの難しさを感じています。

 

情報統計研究所はここから！