情報統計研究所へのアクセスはここから．
PSPP の試用経験(２)
今回は、２×２分割表によるカイ二乗検定の方法を試みます。
PSPP のための演習データファイル（CrossData．sav）を下記 ＵＲＬ より DownLoard して下さい。
http://sky.geocities.jp/dqcdr872/dbase/pspp.html
基本的に前回と同じ方法で、次により行います。
・「File →Open」→「CrossData．sav」
・サンプルデータが「Data View」に表示されます。
・「Variable View」を表示し、「Name」と「Label」を”Mittel”と”Effect”に、
「Measure」を”Nominal”にします。
・「Analyze」→「」Descript Statistics」→「Crosstabs」
・変数選択画面で、「Mittel」→「Columns」、「Effect」→「Rows」
・「statistics」をクリック→「chisq」をチェック→「continue」
・「cells」をクリック→「Count」「Row」「Column」「Total」にチェック→「Continue」
・「OK」
output 画面に結果が出力されます。
データがクロス集計表にまとめられているときは次の様に入力します。
そして、
・「Data」→「Weight Case」→「Frequeny Variable」→「Count」を選択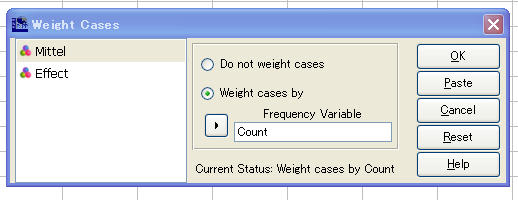
・以下、前記の手順で実行します。
注釈：
やさしい医学統計手法（表８：分割表にまとめられたデータ）から引用。
結果は、
Mittel（偽薬=0、実薬=1）、Effect（無効=0、有効=1）の名義尺度となっています。
精密には、
・補正なし：
X-squared = 12.1979, df = 1, p-value = 0.0004784
・補正あり：
X-squared = 10.151, df = 1, p-value = 0.001442
となり、
偽薬と実薬の効果の割合には統計学的な有意差があり、その効果は偽薬で低く、実薬で高いと判断されます。
詳しくは、「やさしい医学統計手法」（3.1.2 離散量にかかわるとき）の解説を見て下さい。
なお、
「Analyze」→「Non-Parametric Statistics」→「Chi-Square」はカイ二乗の適合度検定です。
「Analyze」→「Descriptive Statistics」（記述統計）では、次の分析が出来ます。
・「Frequency」（度数分布）
・「Descriptive」（記述統計）
・「Explore」（探索的）
・「Crosstabs」（クロス集計表）
次回に続く！
