統計技術 第Ⅲ部:第3章-3:Bias-Reduced Logistic Regression(続き)
統計技術 第Ⅲ部 Free Online Caluclator (例題集)
第3章-3(2):「R」による Penalized regression model の検証
前回の”Free Online Culculator”で紹介した"Bias-ReducedLogisticRegression"は、2値の目的変数のデータ数に大きな違いがある場合などに適用される例題を紹介した.
その際に、
Penalized regression(正則化回帰モデルとも言う)について記述したが、これに対する杉本典夫先生(統計学入門)からのコメントを頂いたので要約して紹介する.
コメントの抜粋:
-------------------------------------------
試験を実施する時は、複数の観察項目間の関連性を説明するために、まず最初に科学的に合理的と思われるモデルを想定します。
そして次に、そのモデルを数学的に近似して解析するために、回帰モデルや相関モデルを当てはめます。
さらに、それらの回帰モデルや相関モデルを用いた解析結果の信頼性が高くなるように、試験デザインと試験の例数を決めて試験計画を立てます。
そしてそれから、実際に試験を実施するのが原則です。
:
後略
-------------------------------------------
このコメントは実験等における大切な原理・原則・・・、でも稀少な臨床実験データ等では、そうも行かない事例が多いのも事実である.
そこで、
「Penalized regression model」とは・・、どの様なものかを「R」を用いた検証を簡単に紹介しよう.
ペナルティ付きロジスティック回帰とは、簡単に言うと、変数が多いためにロジスティック・モデルにペナルティを与えて寄与度の低い変数の係数を縮小させることを回帰係数の制約(正規化)と言っており、1つの変数選択であるかもしれない.
主に、ビッグデータなど機械学数(AI)の分野が対象であり、リッジ回帰(ridge)とラッソ回帰(lasso)が知られている.
そして、変数選択によって最的な回帰モデルを見つけることを、”スパースモデリング(sparse modeling)”と言うなど、機械学習独特の呼び方があるが、ここでは、
単に回帰モデルの係数の違いをデータ解析環境「R」で見てみよう.
例題は、
前回の”Free Online Culculator”で紹介した"Bias-ReducedLogisticRegression"の既存データ(Data X)を選択しExce にペーストし、「R」に読み込んで使用した.ただし、データ数が少ないので、不正確であるかもしれないが、あくまでも1例として体験されたい.
「R」の実行:
------------------------------------------------
dat<- read.delim("clipboard", header=T) # Excel から読込む
head(dat) # 読込んだデータの確認
dx<- data.matrix(dat[,-1]) # X1, X2, X3 のデータマトリクス
dy<- dat[,1] # Y の抽出
head(dy) # Yデータの確認
head(dx) # Xデータの確認
library(glmnet) # ライブラリーを事前にインストールしておく
set.seed(123)
cv.lasso <- cv.glmnet(dx, dy, alpha = 1, family = "binomial") # alpha = 1 は lasso
model.1 <- glmnet(dx, dy, alpha = 1, family = "binomial", lambda = cv.lasso$lambda.min)
coef(model.1) # 係数の出力
cv.ridge <- cv.glmnet(dx, dy, alpha = 0, family = "binomial") # alpha = 0 は ridge
model.2 <- glmnet(dx, dy, alpha = 0, family = "binomial", lambda = cv.ridge$lambda.min) # alpha = 1 は lasso
coef(model.2) # 係数の出力
# 比較のために"brglm"と"glm" の「R」コマンド
attach(dat)
library(brglm) # 事前に"brglm" ライブラリーをインストールしておく
mlb<- brglm(Y~ X1+ X2+ X3, family = "binomial", data=dat)
summary(mlb)
glmModel<- glm(Y~ X1+ X2+ X3, family = "binomial", data=dat)
summary(glmModel)
-----------------------------------
出力結果の係数をまとめると図1のようになった.
図1 各回帰モデルの係数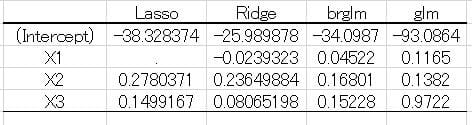
Lasso ではX1が除外され、通常のロジスティック回帰モデル(glm)ではX3の値が他に比較して大きく、係数の比重が大きいことが分かる.
このことから、
目的変数(Y)の2値のデータ数に大きな違いがあると・・、すなわち、バイアスが大きいと回帰モデルに影響を与えるので、注意すべきことが分った.
ただし、
この例題のデータ数自体が少数であるので、不正確であるかも知れないので留意されたい.


















