統計技術 第Ⅲ部 Free Online Caluclator (例題集)
第3章-3:Bias-Reduced Logistic Regression(ロジスティック回帰)
ロジスティック回帰分析は、多くの場合名義尺度(0, 1))からなる2値の目的変数に対して適用されるが、
2値のデータ数に大きな違いがある場合などは、DavidFirth(英国の統計家)によって提案された"Bias-ReducedLogisticRegression"を用い、推定値と標準誤差の修正することがある.
したがって、よく用いられる "Logistic Regression"の結果とことなるので、データ数に大きなバイアスがなければ、通常の方法で良い.
ここで紹介する方法はデータ数に大きなバイアスがあるときの方法である.
それでは、
下記のURLで試してみよう.
使用する Free Online Calculator :
● Free Statistics Software (Calculator) - Web-enabled scientific services & applications
https://www.wessa.net
上記URLのトップページから、
↓
Regression Software
↓
Logistic Regession
↓
[Data X]を確認
↓
Compute をクリック
出力結果:
-------------------------------------
図1 推定値などの統計量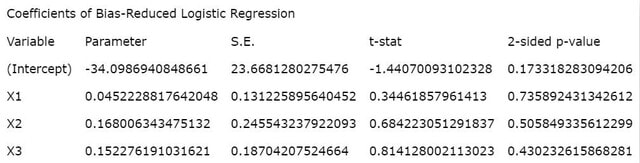
図2 統計量の記述
ここで、
Deviance とは、回帰モデルの適合性統計(逸脱の指標)であり、すなわち、モデルへのフイティング(当てはめ)の良さを表す.
また、
Penalized regression(正則化回帰モデルとも言う)とは、制約付き最小二乗法や罰則化回帰モデルとも呼ばれるもので、通常の最小二乗法では、説明変数が増えると過学習してしまうことがある.
予測モデルは未知のデータに対して既存のデータから学習した推定式による予測の当てはまり(フイティング)をよくすることであるが、学習データを過剰に学習して、かえって、未知のデータへの当てはまりを悪くしている場合があり、これを過学習と言っている.
すなわち、
必要以上の説明変数を用いることで、かえって予測の精度を悪くしている場合がある.
これを防ぐために、変数選択をしたりするが、その1つの方法として正則化項を入れた"Penalized regression model"がある.
ここでは、
専門的な詳細は割愛するので、専門書やWebサイトを参照されたい.
「参照」
統計技術 第11章-5 ロジスティック回帰分析
http://toukei.sblo.jp/article/188015481.html
また、
ホスマー・レメショウ検定( Hosmer-Lemeshow test)もロジスティック回帰モデルへの適合度を調べる統計学的検定である.
図3 ROC曲線
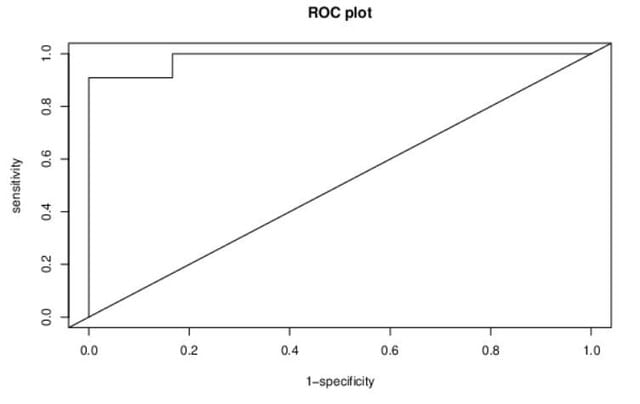
ここでのROC 曲線はかなり大雑把であるので、下記のサイトを紹介しておこう.
情報統計研究所(やさしい医学統計手法)「9.6. ROC(Receiver Operating Characteristic)について」
http://kstat.sakura.ne.jp/medical/med_038.htm


















