情報統計研究所へのアクセスはここからお気軽に
主成分回帰分析(Pricipal Component Regression)について。
図1は主成分分析での第1主成分(COMP-1)と第2主成分(COMP-2)の主成分スコアを2次元座標にプロットしたものです。
図1 主成分スコアー散布図
図1では明らかに2つの群に分かれており特徴的な散布図です。この散布図のデータは表1のようになっています。
表1:主成分分析に用いたデータ
表1の変数(status)は目的変数であり、ここでは、細胞とか微生物とか何らかの計測値の結果(good=0、poor=1)を、そして、「w1~w4」は週単位などの時間を表しています。
主成分分析結果は表2の通りであり、主成分負荷量と寄与率を示しました。
表2 主成分負荷量と寄与率
図1と表2から、ここでのデータの寄与率は十分に大きなCOMP-1 と COMP-2 で説明できそうです。主成分回帰(PCR)は、
ここでの COMP-1 の主成分スコアを説明変数として重回帰型分析を行ったものです。
ここでは、
目的変数(status)が「0」と「1」の2値ですので、logistic 回帰分析を適用します。
「R」プログラムの環境があれば、次の様になります。
pcr<- princomp ( mydata , cor = TRUE )
summary ( pcr , loading=TRUE )
comp.1<- pcr$scores [ , 1 ]
logit.model<- glm ( status ~ comp.1, binomial , data=mydata)
summary ( logit.model )
この結果は表3に示したようになりました。
表3 「R」の出力結果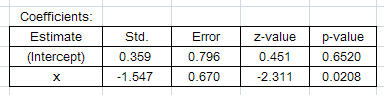
さて・・・、
重回帰分析では多重共線を問題にしていました・・・、そうです、相関の強いものは除くのでした・・・。
ここでのデータは status を時間経過で計測していますので、当然、w1~w4 の相互間には強い相関関係が見られます。
多重共線性を無視して良いのでしょうか・・・
次回に続く!


















