統計技術:第8章 要約統計量による効果量の計算(続き)
第8章-3:要約統計量(Summary)による効果量(続き)
引き続き、
下記URLのUCCS(Free Online Calcultoer)を使って効果量(ES:Effect Size)を求める方法の紹介です。
https://www.psychometrica.de/effect_size.html
上記URLから、下記を選択してみて下さい。
#5. Calculation of d and r from the test statistics of dependent and independent t-tests.
ここでの効果量は、スチューデント t 検定などの仮説検定からの検定統計量を使用して取得することもできます。独立したサンプル(Independent t-test)の場合、結果は本質的に効果サイズの計算「#2 」と同じです。
例題は、
「統計のコツのこつ(31)」の要約統計量(summary data)を用いてみましょう(下記URL)。
https://blog.goo.ne.jp/k-stat/e/3ce0391051242c38d99a3a925be39d22
Summary data は次の通りです。
...........mean.......sd..........n........t-value
A 群....122.5......10.85.....30.......3.3062
B 群....133.4......12.25.....20
そでれは、上記「#5」を選択し、上記のsummary data を図1のように入力してみましょう。
図1 「#5」(independent の場合)の入力と出力結果
Effect Size d = 0.954 となっており、
この値は、もともと、"Hedges" と "Olkin" は 修正された効果の大きさ "d" とも呼んだようで、いまだに混乱しているようです。
ここでの効果量は 1980 年代初頭から "g" と呼ばれており、最初に修正措置を提案した著者 Glass (Ellis, 2010) に由来しています。
このロジックに従って、"gHedges" は "g" ではなく" h" と呼ぶ必要がありまが、 通常、これは単純に "dCohen" または "gHedges" と呼ばれ、修正された測定値であることを示しています。
近似的に次式により"Cohen's d"を知ることができます。
d= t* sqrt(1/n1+ 1/n2)= 0.954
次に、
図1の「Mode of testing」で「dependent」を選べば、対応のあるt検定(Paired t-test)の効果量を知ることができます。
Summary data は次の通りです。
............mean.......sd..........n........t-value
Pre......207.93.....28.56.....15........6.6897
Post.....197.........24.39
図2 「#5」(dependent の場合)の入力と出力結果
例題(図1)の原データは図3のとおりです。
図3 例題の原データ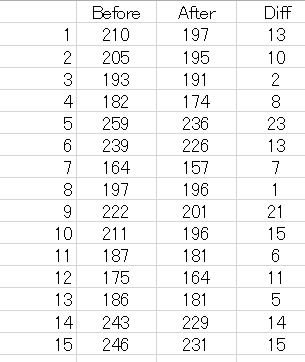
原データから計算した結果は図4のとおり、Summary の結果と一致しています。
図4 原データから計算した結果
"Free Online Calculator"(Statistics Kingdom)の結果。
しかし、
"summary data" による計算は、近似的な計算がなされている場合が多く、また、計算上の丸めなどで、必ずしも正確とは言えない場合がありますので、使用に当たってはご注意下さい。
次回の続く!
文責:
ISL assistant staff "KUMI"









