統計技術:第8章 要約統計量による効果量の計算(続き)
第8章-5:要約統計量(Summary)による効果量(続き)
下記URL(UCCS:Free Online Calcultoer)から、
https://www.psychometrica.de/effect_size.html
「#11. Effect size calculator for non-paraetric tests Mann-Whitney, Wilcoxon and Kruskal Wallis-H」を選択し、
代表的なノンパラメトリック検定の効果量を求めてみましょう。
図1 「#11」の画面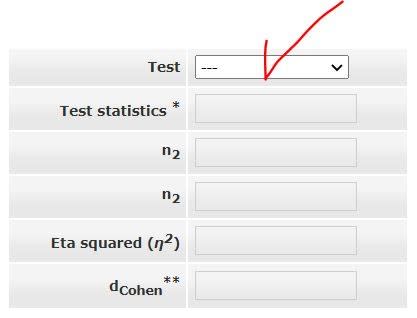
ここでは、η2 を計算するために、ウィルコクソンの符号順位検定、Mann-Whitney-U または Kruskal-Wallis-H の検定統計量から効果量を知ることができます。
赤矢印から「Test」方法を選択します。
「Test」方法は次の通りです。
・ Mann-Whitney-U
・ Wilcoxon-W → Wilcoxon signed-rank test(対応のある2群の検定)
・ Kuraskall-Wallis-H
簡単な例題「Gooブログ:統計のコツのこつ(34)」でやってみましょう。
https://blog.goo.ne.jp/k-stat/e/5902206eb2209b533f99ec160f0d6a7a
● 「マンーウイットニー順位のU検定の方法(Mann-Whitney-U test)」です。
図2 「Mann-Whitney-U」のための例題
このデータの検定結果は次の通りです。
U値=89
p値=0.00278
n1=20、 n2=20
よって、下記(図3)のように入力します。
図3 入力と出力の画面
「Eta squared(η^2)=0.225 → Eta(η)=√0.225≒0.47 (Eeffect size)」となります。
次に、
● 「ウイルコックスンの符号順位和検定の方法(Wilcoxon signed rank test)」(対応のある2群の有意差検定)です。
簡単な例題「Gooブログ:統計のコツのこつ(35)」でやってみましょう。
https://blog.goo.ne.jp/k-stat/e/4d607c86ceb4c03c8d3fea2991a2ad49
図4 「Wilcoxon-W」のための例題
このデータの検定結果は次の通りです。
W値=182
Z値 =3.485892
P値=0.00049
N=19
ここではZ値を用い、下記(図5)のように入力し効果量(η^2)を求めてみましょう。
図5 入力と出力の画面
「Eta squared(η^2)=0.64 → Eta(η)=√0.64=0.8(Eeffect size)」となります。
なお、
商用統計ソフトでは、「Rank-Biserial Correlation Coefficient 」(双列相関係数)で表している場合があります。
例えば、
「Wilcoxon signed rank test」の場合だと、
Rank-Biserial Correlation Coefficient≒0.92 となります。
次に、
●「クラスカル-・ウォ-リスの検定(Kruskal-Wallis-H test)」です。
簡単な例題「Gooブログ:統計のコツのこつ(38)」でやってみましょう。
https://blog.goo.ne.jp/k-stat/e/9e6499b621d713d75832ae004f14b784
図6 「Kruskal-Wallis-H」のための例題
このデータの検定結果は次の通りです。
H値=10.312
P値=0.0058
N=18
よって、下記(図7)のように入力します。
図7 入力と出力の画面
「Eta squared(η^2)=0.554 → Eta(η)=0.744(Eeffect size)」となります。
***
統計技術は終了します。
執筆は途中から情報統計研究所(アシスタントの”KUMI”)が担当しました。










