母方のいとこが定期的に集まり、一泊の旅行をするいとこ会、名称は「こすもす(秋桜)会」を続けている。”こすもす”という名前は、母の実家の姓から”秋”という1字を採ったものである。
こまめな幹事役のSさんたちが、祖父母、親、子世代を含む四世代の名簿を作ってくれていて、ここには、祖父母に始まり、9人の親世代、18人の我々いとこ世代、そして36人の子供世代の名前が記されている。各世代の配偶者を合わせて、合計91名の名前と生(没)年月日をここに見ることができる。

大阪・箕面でのいとこ会の余興風景(2009.10.16 撮影)

大阪・箕面でのいとこ会参加の女性陣(2009.10.17 撮影)
二年ほど前に、鹿児島に住んでいる従弟と、その姉の従妹とその娘の3人が私の母を訪ねて大阪に来たことがあった。
その時、この「いとこ会」のことが話題になり、従弟のYさんが「いとこ会の名簿を見ていると、同じ誕生日のペアがたくさんあって、少し不思議に思う」と話した。
実は、私も同じことを感じていて、確率論的にみてどんなものか計算してみたいと思っていたのだが、その時はどのような計算をすればいいのかすぐに思いつかず、そのままになっていた。今回思い立ってこれを実行することにした。

淡路島でのいとこ会(2010.11.26 撮影)

淡路島でのいとこ会(2010.11.27 撮影)
名簿に名前のある91人の中に、誕生日が同じペアが11組存在している。その内、一組は双子で、私の母とYさんの母である。また、叔父の一人だが夫婦で同じ誕生日、それも年月日すべてが同じという組もある。
双子のケースを他のケースと同様に扱っていいものかどうか、疑問の残るところであるが、とりあえず91人の集団に、11組の誕生日が同じペアがいる確率を計算してみることとした。
この計算は意外に面倒である。

叔母のマジックショウ(2012.3.17 撮影)
ウィキペディアには、「誕生日のパラドックス」というページがあって、ここで誕生日が同一の2人(以上)がいる確率を議論している。集団の人数と、その中に誕生日が同じ2人が見つかる確率のグラフは次のようである。これによると、70人しか集まらなくてもその確率は99.9%を超え、50%を超えるのに必要な人数は、わずか23人で、その時の確率は50.7%(0.507)であるとしている。集団の中に、同じ誕生日の2人が見つかる確率は、意外に高いのである。
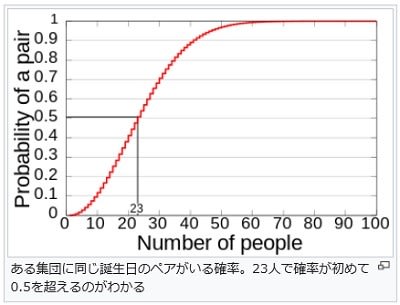
ある集団に同じ誕生日のペアがいる確率(ウィキペディア「誕生日のパラドックス」
⦅2017年9月28日 (木) 09:16⦆より)
ここで、パラドックスという言葉は、論理的な矛盾に基づいているという意味でのパラドックスではなく、結果が一般的な直感と反しているという意味でのパラドックスであるとしているが、確かに、誕生日の数が(閏年は除くとして)365種類あることを考えると、上の確率計算結果は直感とは合致しないように思える。
ところで、ここで採用されている計算は、誕生日が同一の2人以上がいる確率であり、誕生日が同一の2人が一組だけ見つかる確率ではない。計算方法は下記のようなもので、余事象を用いて行われていて、上記のように直感との比較をするのであれば、これでいいのかもしれないが、今私が求めようとしている目的には使えないと思われた。
ウィキペディアを始めとして、ネットを検索して見つけることができるもののほとんどは、n人の中で同じ誕生日の人が少なくとも2人いる場合の確率P2を計算で求めていて、その方法は、n人の誕生日が全て異なる場合の確率p1を計算して、この確率を1から引くという方法である。
p1(n) = 364/365x363/365x362/365x・・・・x(365-n+1)/365 = 365!/365^nx(365-n)!
p2(n) = 1-365!/365^nx(365-n)!
となって、n=23のとき、p2=0.507・・となり、50%を超えるという訳である。

有馬温泉でのいとこ会余興風景(2013.11.3 撮影)

有馬温泉でのいとこ会参加メンバー(2013.11.4 撮影)
では、誕生日が同一の2人が複数組見つかる確率を計算するには、どうすればいいか。余事象によらない、直接事象計算をする別な計算式を使わなければならない。この場合の方法として、トランプのポーカーの手ができる確率計算の方法などがあり、これらを参考にすると次の確率計算の方法が適当と思われた。
n人の中で同じ誕生日の人が一組だけ見つかる確率の計算法は、n人から2人を選ぶパターン数をXとして、誕生日のパターン数Yは365であり、2人のペア以外の(n-2)人の誕生日のパターン数Zは、先の2人とは重複しないように順次選ぶと、
X = n(n-1)/2, Y = 365, Z = (365-1)(365-2)・・・(365-n+2)
であり、これらすべての積を、すべての誕生日のパターン数Wで割ることで、その確率が得られる。
W=365^n
であるから、n=23 の場合の結果は
XxYxZ/W=0.363
である。この値はウィキペディアが示す、少なくとも一組の同じ誕生日のペアが見つかる確率 0.507に比べるとだいぶ小さい値になるが、ウィキペディアの場合には同じ誕生日の組み合わせの、他の多くのパターンが含まれていたことを考えれば理解できるであろう。
では、91人の中で同じ誕生日のペアが11組見つかる確率はどうなるか、同じ方法を用いて計算してみる。計算の方法は、91人から2人のペアを11組選ぶパターン数をXとして、誕生日のパターン数Yを365,364・・・と11組に対して順次減らし、2人のペア以外の(91-22)人の誕生日のパターン数Zは、先の22人、11組とは重複しないので、
X = 91(91-1)/2x(91-2)(91-3)/2x・・・x(91-20)(91-22+1)/2/11!, Y = 365x(365-1)x・・・x(365-11+1), Z = (365-11)x(365-12)x・・・x(354-91+23), W = 365^91
であるから、計算するとその確率は、
XxYxZ/W = 0.054
という結果になる。
さて、この約5%強という結果をどう見ればいいのか。迷うところであるが、かなり珍しいということになるのではないだろうか。従弟のYさんと私の直感は当たっていたということになるのかもしれない。

淡路島のイングランドの丘でコアラを見る(2015.10.4 撮影)

鳴門でのいとこ会参加メンバー(2015.10.4 撮影)
ところで、今回誕生日が同じ人のペアが多数見つかることを共に指摘したYさんと私であるが、我々の母親は双子であった。昨年私の母が亡くなり、すでに二人ともこの世にはいないのだが、この双子の叔母と母のそれぞれの子供を見ると、叔母の子供は、女(3=女・女・男)・女(2=女・男)・男(2=女・女)の3人、母の子供は、男(2=男・女)・女(3=女・女・女)・女(2=男・女)の3人と順番が異なるが共に女2人と男一人の3人である。またそれぞれの孫の数も()内に示した通りで、女5人、男2人と同じになっている。更に、叔母の長女の娘の一人と私の娘の職業が共にCAであった。
大正生まれの私の母と、叔母とは双子として生まれたが、生後すぐに私の母は養女として、祖父母の友人の家にもらわれていった。満州でのできごとであった。その後、母は自らが双子であったことを知らずに、一人っ子だと思って育ったという。結婚後に、或ることから自分には双子の妹がいることを知ったが、その時にはその妹は、鹿児島の枕崎に嫁ぎ、暮らしていた。
このように、遠く離れ育った双子の2人の家族の間に、いくつかの共通点があることにも、確率論的な興味がわく。叔母と母とは、後年近畿大学と東京大学の双子を研究するチームからの依頼があって、協力していたと聞いたことがある。一体どのような調査であったのか知りたくなってくるのであるが。
妻に、妻の側にも私の場合と同じような資料があるかと聞いたが、そんなものはないという。91人もの親類の生年月日の判る名簿があることのほうが、よほど珍しいということらしい。
こまめな幹事役のSさんたちが、祖父母、親、子世代を含む四世代の名簿を作ってくれていて、ここには、祖父母に始まり、9人の親世代、18人の我々いとこ世代、そして36人の子供世代の名前が記されている。各世代の配偶者を合わせて、合計91名の名前と生(没)年月日をここに見ることができる。

大阪・箕面でのいとこ会の余興風景(2009.10.16 撮影)

大阪・箕面でのいとこ会参加の女性陣(2009.10.17 撮影)
二年ほど前に、鹿児島に住んでいる従弟と、その姉の従妹とその娘の3人が私の母を訪ねて大阪に来たことがあった。
その時、この「いとこ会」のことが話題になり、従弟のYさんが「いとこ会の名簿を見ていると、同じ誕生日のペアがたくさんあって、少し不思議に思う」と話した。
実は、私も同じことを感じていて、確率論的にみてどんなものか計算してみたいと思っていたのだが、その時はどのような計算をすればいいのかすぐに思いつかず、そのままになっていた。今回思い立ってこれを実行することにした。

淡路島でのいとこ会(2010.11.26 撮影)

淡路島でのいとこ会(2010.11.27 撮影)
名簿に名前のある91人の中に、誕生日が同じペアが11組存在している。その内、一組は双子で、私の母とYさんの母である。また、叔父の一人だが夫婦で同じ誕生日、それも年月日すべてが同じという組もある。
双子のケースを他のケースと同様に扱っていいものかどうか、疑問の残るところであるが、とりあえず91人の集団に、11組の誕生日が同じペアがいる確率を計算してみることとした。
この計算は意外に面倒である。

叔母のマジックショウ(2012.3.17 撮影)
ウィキペディアには、「誕生日のパラドックス」というページがあって、ここで誕生日が同一の2人(以上)がいる確率を議論している。集団の人数と、その中に誕生日が同じ2人が見つかる確率のグラフは次のようである。これによると、70人しか集まらなくてもその確率は99.9%を超え、50%を超えるのに必要な人数は、わずか23人で、その時の確率は50.7%(0.507)であるとしている。集団の中に、同じ誕生日の2人が見つかる確率は、意外に高いのである。

ある集団に同じ誕生日のペアがいる確率(ウィキペディア「誕生日のパラドックス」
⦅2017年9月28日 (木) 09:16⦆より)
ここで、パラドックスという言葉は、論理的な矛盾に基づいているという意味でのパラドックスではなく、結果が一般的な直感と反しているという意味でのパラドックスであるとしているが、確かに、誕生日の数が(閏年は除くとして)365種類あることを考えると、上の確率計算結果は直感とは合致しないように思える。
ところで、ここで採用されている計算は、誕生日が同一の2人以上がいる確率であり、誕生日が同一の2人が一組だけ見つかる確率ではない。計算方法は下記のようなもので、余事象を用いて行われていて、上記のように直感との比較をするのであれば、これでいいのかもしれないが、今私が求めようとしている目的には使えないと思われた。
ウィキペディアを始めとして、ネットを検索して見つけることができるもののほとんどは、n人の中で同じ誕生日の人が少なくとも2人いる場合の確率P2を計算で求めていて、その方法は、n人の誕生日が全て異なる場合の確率p1を計算して、この確率を1から引くという方法である。
p1(n) = 364/365x363/365x362/365x・・・・x(365-n+1)/365 = 365!/365^nx(365-n)!
p2(n) = 1-365!/365^nx(365-n)!
となって、n=23のとき、p2=0.507・・となり、50%を超えるという訳である。

有馬温泉でのいとこ会余興風景(2013.11.3 撮影)

有馬温泉でのいとこ会参加メンバー(2013.11.4 撮影)
では、誕生日が同一の2人が複数組見つかる確率を計算するには、どうすればいいか。余事象によらない、直接事象計算をする別な計算式を使わなければならない。この場合の方法として、トランプのポーカーの手ができる確率計算の方法などがあり、これらを参考にすると次の確率計算の方法が適当と思われた。
n人の中で同じ誕生日の人が一組だけ見つかる確率の計算法は、n人から2人を選ぶパターン数をXとして、誕生日のパターン数Yは365であり、2人のペア以外の(n-2)人の誕生日のパターン数Zは、先の2人とは重複しないように順次選ぶと、
X = n(n-1)/2, Y = 365, Z = (365-1)(365-2)・・・(365-n+2)
であり、これらすべての積を、すべての誕生日のパターン数Wで割ることで、その確率が得られる。
W=365^n
であるから、n=23 の場合の結果は
XxYxZ/W=0.363
である。この値はウィキペディアが示す、少なくとも一組の同じ誕生日のペアが見つかる確率 0.507に比べるとだいぶ小さい値になるが、ウィキペディアの場合には同じ誕生日の組み合わせの、他の多くのパターンが含まれていたことを考えれば理解できるであろう。
では、91人の中で同じ誕生日のペアが11組見つかる確率はどうなるか、同じ方法を用いて計算してみる。計算の方法は、91人から2人のペアを11組選ぶパターン数をXとして、誕生日のパターン数Yを365,364・・・と11組に対して順次減らし、2人のペア以外の(91-22)人の誕生日のパターン数Zは、先の22人、11組とは重複しないので、
X = 91(91-1)/2x(91-2)(91-3)/2x・・・x(91-20)(91-22+1)/2/11!, Y = 365x(365-1)x・・・x(365-11+1), Z = (365-11)x(365-12)x・・・x(354-91+23), W = 365^91
であるから、計算するとその確率は、
XxYxZ/W = 0.054
という結果になる。
さて、この約5%強という結果をどう見ればいいのか。迷うところであるが、かなり珍しいということになるのではないだろうか。従弟のYさんと私の直感は当たっていたということになるのかもしれない。

淡路島のイングランドの丘でコアラを見る(2015.10.4 撮影)

鳴門でのいとこ会参加メンバー(2015.10.4 撮影)
ところで、今回誕生日が同じ人のペアが多数見つかることを共に指摘したYさんと私であるが、我々の母親は双子であった。昨年私の母が亡くなり、すでに二人ともこの世にはいないのだが、この双子の叔母と母のそれぞれの子供を見ると、叔母の子供は、女(3=女・女・男)・女(2=女・男)・男(2=女・女)の3人、母の子供は、男(2=男・女)・女(3=女・女・女)・女(2=男・女)の3人と順番が異なるが共に女2人と男一人の3人である。またそれぞれの孫の数も()内に示した通りで、女5人、男2人と同じになっている。更に、叔母の長女の娘の一人と私の娘の職業が共にCAであった。
大正生まれの私の母と、叔母とは双子として生まれたが、生後すぐに私の母は養女として、祖父母の友人の家にもらわれていった。満州でのできごとであった。その後、母は自らが双子であったことを知らずに、一人っ子だと思って育ったという。結婚後に、或ることから自分には双子の妹がいることを知ったが、その時にはその妹は、鹿児島の枕崎に嫁ぎ、暮らしていた。
このように、遠く離れ育った双子の2人の家族の間に、いくつかの共通点があることにも、確率論的な興味がわく。叔母と母とは、後年近畿大学と東京大学の双子を研究するチームからの依頼があって、協力していたと聞いたことがある。一体どのような調査であったのか知りたくなってくるのであるが。
妻に、妻の側にも私の場合と同じような資料があるかと聞いたが、そんなものはないという。91人もの親類の生年月日の判る名簿があることのほうが、よほど珍しいということらしい。
















