昨年からガラスショップをオープンして、日々仕入れ・売上げ・在庫の管理と数字との格闘が続いていて、3月には青色申告と確定申告をしなければならず、慣れないことに大いに悩まされたが、今はそれも済んでほっと一息という状態である。ただ、もともと数字を眺めたり扱うことは嫌いではなくむしろ好きな方なので、こうした作業を楽しんでいるというところもある。
小学生のころ、親から「学習百科」という名前だったと思うが、主要教科に関するあれこれが書かれた分厚い本を買ってもらって隅から隅まで熱心に読んだ記憶がある。その中の算数の部分に、自然数、素数といった言葉のほかに、2、3、4、5、などの数で割り切れる大きな自然数の見分け方といったことや、魔方陣の作り方が解説されていて興味深く読んだ。3で割り切れる数、すなわち3の倍数の見分け方は、もちろんご存知の方も多いことと思うが、各桁の数字を加えてその合計が3の倍数になれば、元の大きな数も3で割り切れるというものであり、子ども心にとても感心した。たとえば、
12345という数はは各桁の合計が1+2+3+4+5=15で3の倍数なので、12345÷3=4115と割り切れるが、23456の場合は、2+3+4+5+6=20なので、23456÷3=7818・・・2と割り切れず、3の倍数ではないといったぐあいである。
もう一つの、魔方陣というのは3x3、4x4,5x5・・・のマス目にそれぞれ1~9、1~16、1~25・・・までのすべての数字を入れて、タテ・ヨコ対角の数字の合計がどこも同じ値になるように配置したもので、自分で考えて作ろうとすると、なかなかむつかしいのだが、本に書かれている方法だと3x3や5x5などの奇数x奇数のマス目の場合は簡単に作れてしまうので大いに感心したのであった。
奇数x奇数のマス目の魔方陣の作り方については、ご存知の方も多いと思うが、次のように書かれていたことを覚えている。解法は、すべて共通しているが、3x3のマス目の場合で言うと、次の図の右側のように、中央の行と列をひとマスだけ外にはみ出させてできるひし形のマス目に、一番上から左下(右下でもいいが)に向かって1から順に3まで数字を置いてゆき、4は1の右下(左下)に置いてまた同じように6までを置く、7から9までも同様にしてマス目を埋め終わったら、外にはみ出している数字を、3x3のマス目内に戻す作業をする。その時のルールは矢印で示したように上下左右に移動させるが、一番遠い位置に戻すのである。
5x5のマス目の場合でも、ルールは全く同様なので確認していただければと思う。ただし、はみ出させるマス目の数は変化する。

3X3マス目の魔方陣の答え(左)と作り方(右)、タテ・ヨコ対角の数字の合計はすべて15になる

5X5マス目の魔方陣の答えの1例(左)と作り方(右)、タテ・ヨコ対角の数字の合計はすべて65になる
3x3のマス目の魔方陣は上下・左右の対称的配置は除くと、答は上記の配列だけである。一方、5x5のマス目の魔方陣については答は非常に多く、2億7530万5224通りあるとされている。上記解法で得られるものは、その1例に過ぎない。
4x4のマス目の魔方陣についての解法は出ていなかったように思うが、正確な記述についてはもう忘れてしまった。この4x4のマス目の魔方陣の答えは880通りあるとされているが、答えの一例は次のようなものである。
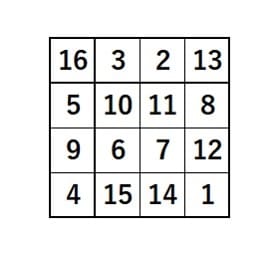
4X4マス目の魔方陣の答えの1例、タテ・ヨコ対角の数字の合計はすべて34になる
7x7のマス目の場合の解法も基本的に同じであるが。外にはみ出ている数字を戻す場合に、一番遠い位置という考えはできなくなるので、下図のように同じ色で示した2つの数字はそのまま一緒に同じ色の場所へ上下左右に移動させることで成立する。

7X7のマス目の魔方陣の答えの1例(左)と作り方(右)、タテ・ヨコ対角の数字の合計はすべて175になる
魔方陣に関する情報を検索していくと、更に大きなマス目の魔方陣や複雑なものも見られるが、この話題はこれくらいにしておく。
上記のマス目の問題は、自然数nの2乗に関する話ということもできるのであるが、これについてもう一つ興味深い話題がある。これは、知人の書いた「Why? 数の不思議あそび」(北川恵司著 2007年サイエンステイスト発行)で紹介されているものであるが、自然数nの2乗の数が見せるちょっと不思議な話題である。
10の2乗=100、11の2乗=121、12の2乗=144 といっても何の不思議もないが、これらの右辺の合計を見ると、100+121+144=365となり、どこかで見た数字になる。そう、1年の日数と一致している。話はこれだけで終わらない、続く13の2乗=169、14の2乗=196を見ると、169+196=365と再び365が登場する。これは何故か。もちろん数字の世界と、地球が太陽の周りを公転する周期と自転周期の比である1年の日数との間に関係などあるはずもなく、偶然の一致ということになろうが、数字の世界と自然界のもつ数値との関係を感じさせるということでちょっとした不思議である。
話は少し飛ぶが、数字と自然・宇宙との間にはなにか特別な関係が存在しているのではないだろうかという問題を考えた数学者は数多くいて、その究極が今からちょうど160年前に提出され、未だに解かれていないという数学史上最大の難問「リーマン予想」ということになる。
昨年2018年9月に、1859年に提出されたこのリーマン予想の証明が行われたとの報道がなされたが、数学の証明が正式に認められるまでには、2年間をかけての検証が必要とされているから、現時点ではまだ何とも言えない。
1,2,3,4,5,6,7,8,9,10・・・と続く自然数。その中には素数が含まれている。素数という数は1またはそれ自身以外に約数を持たない自然数ということになるが、2,3,5,7,11,13,17・・・という小学校で学ぶ数列である。この素数の謎を解明しようとした何人もの天才数学者の取り組みの中から生まれてきたのが、この「リーマン予想」だったということもできる。
もうずいぶん前にNHKのTV番組で素数問題に取り組む数学者をとりあげたことがあった。とても興味深い内容であったので、今もその放送を録画したディスクを大切に持っている。放送は2回、別々の番組として行われたが、内容はほぼ同じであった。探し出してみると「魔性の難問~リーマン予想・天才たちの戦い~」、「素数の魔力に囚われた人々~リーマン予想・天才たちの150年の闘い」というタイトルでそれぞれ、2009.11.15日と2009.11.21日に放送されたものの録画であった。
この放送はご覧になった方もおられることと思うが、次のような内容であった(今はYouTube で見ることができる)。
2,3,5,7,11,13,17・・と無限に続く素数には一見何の規則もなくランダムに出現しているように思える。素数であることを確認しながら、ずっと自然数を追っていくと次々と素数が見つかる場所があるかと思うと、しばらくは全く素数が現れない場所もあって、規則性などまったくないように思える。
しかし、この素数にはなにか宇宙の秘密が隠されているのではと直感的に感じた数学者もいて、根気よく素数を調べていった。その一人が、1700年代のスイス人の天才数学者・天文学者と言われているオイラー(1707.4.15~1783.9.18)であった。
彼は素数だけを用いた次のような数式(オイラー積)を考えてみた。するとその結果は収束して円周率π(パイ)の2乗を6で割った数字になることを見出した。このことからやはり素数にはなにか大自然とのつながりのある秘密が隠されているのではないかとの確信を深めていったが、当時はそれ以上進むことはなかった。

オイラーの肖像(ウィキペディアから)
次に番組で紹介されているのは、やはり天才数学者・天文学者・物理学者といわれたドイツ人ガウス(1777.4.30~1855.2.23)である。彼は15歳の頃、毎日1000個の自然数を検証することを自らに課し、その中にいくつの素数が含まれているかを数えたとされているが、その結果300万までの自然数のなかの素数を確認したとされている。

ガウスの肖像(ウィキペディアから)
一方、彼が素数の秘密に迫るために採ったアプローチは、自然対数表を用いるもので、見つかった素数Pをその素数の自然対数で割り答えQを求め、これをPが何番目の素数であるかを示すRと比較していった。素数Pが小さい間はQとRは一致せず、例えば素数9227に対するQ=1010、R=1144という具合であったが、次第に大きい素数になっていくにしたがって、素数262069の場合には、Q=21005、R=22992と、次第に両者の誤差が小さくなり、最終的にはQ=Rに収束するという発見をする。
このことは、素数が自然対数の底であるe(ネイピア数、=2.7182818284・・・)という、自然界でπ(パイ)と並んで最も重要な定数と関係していることが示された。
ガウスから約50年後に登場するのが、リーマン予想を提出したドイツ人の数学者リーマン(1826.9.17~1866.7.20)その人である。彼はオイラーやガウスの採ったアプローチに不満があったとされ、もっと数学的に厳密な方法で素数の並びに意味があるかどうかを調べようとして、オイラーが用いた式を少し変えた式リーマンゼータ関数というものを考案した。次のようなものである。

リーマンゼータ関数
この関数がゼロになる点、すなわち「ゼロ点」を先ず4つほど求めてみたところ、予想外の結果が得られた。4個のゼロ点は一直線上に並んでいた。

リーマンの肖像(ウィキペディアから)
TV放送では特に触れられていなかったが、この関数の変数は複素数で、ゼータ関数がゼロになる位置=ゼロ点は複素平面上の直線上に並んでいるということになる。
この結果を見て、リーマンはこのあと何人もの天才数学者の人生を翻弄することになる「リーマン予想」を提出することになる。それは次のようである。
リーマン予想:「ゼータ関数の非自明なゼロ点はすべて一直線上に並ぶはずだ」
ここで、非自明という言葉が使われているのは、自明なゼロ点というものも存在するからであるが、ここではこれ以上は触れない。
リーマンは、このリーマンゼータ関数のゼロ点という概念を素数の問題に取り込むことによって、「素数の並びには意味があるか」という漠然とした問題を素数だけからなる「ゼータ関数のゼロ点は直線上にだけ現れるか」という数学的な問題に置き換えることに成功した。
番組ではこのあと1950年代に、リーマン予想を証明しようと取り組んだ天才数学者を紹介していくが、かれらは次々と挫折し、その人生を狂わせていく。この挑戦者とは次のような人々である。
・ゴッドフレイ・ハーディー(1877.2.7~1947.12.1 英国・数学者)
・ジョン・リトルウッド(1885.6.9~1977.9.6 英国・数学者)
・ジョン・ナッシュ(1928.6.13~2015.5.23 アメリカ・数学者)
・アラン・チューリング(1912.6.23~1954.6.7 英国・数学者、論理学者、暗号解読者、コンピュータ学者)
3人目のジョン・ナッシュ博士は、1994年のノーベル経済学賞を受賞しているが、リーマン予想に取り組む中で、精神を病んでいく物語は、「ビューティフル・マインド」という映画に描かれたという。後年、ナッシュ博士は「数学的に考えるということは、心の内面に向き合うことであり、ある時には論理的にあるときは非論理的に考える必要があり、そうして心を病んでいった。」と振り返っている。
リーマン予想に取り組んだ数学者の多くは、自らも素数と自然界のつながりを信じ、これを証明しようとした。しかし、4人目の第二次大戦中にナチスドイツのエニグマ暗号を解読したことで知られるチューリング博士の場合は違っていた。彼は、素数の並びに意味があるとは信じておらず、ゼータ関数の4個のゼロ点が乗っている直線上以外の場所にあるセロ点をコンピュータを駆使してしらみつぶしに探していった。しかし、3カ月かけて1000個以上のゼロ点を見つけたものの、これらはすべて直線上にあり、直線の周辺にはまったく見つからなかった。さらにその後、チューリング博士は謎の死を遂げるという不幸に見舞われる。
仮に1個でも直線から外れた場所にゼロ点を見つけることができれば、リーマン予想はその意味を一気に失うことになったのであるが・・・。
このように不幸な出来事が続いた結果、リーマン予想に取り組むこと、あるいは取り組んでいるということを知られることは数学会のタブーのようになっていく。
放送で、その挑戦者の最後の一人として紹介されているのが、すでに数学の分野で多くの業績を挙げてきているフランス人数学者のルイ・ド・ブランジェ博士(放送当時77歳、1932.8.21~)であった。博士もまた素数と自然界との間の強い関係を信じ、独自の見解を持ち、素数を研究していた。それは素数は原子や素粒子などのミクロの世界とつながっているはずだというものであった。

ド・ブランジェ博士(ウィキペディアから)
この素数とミクロの世界とのつながりは、その後劇的なかたちで展開を見せる。舞台はヨーロッパからアメリカに飛ぶが、プリンストン高等研究所のお茶の時間に数学者ヒュー・モンゴメリ博士(ミシガン大学教授)と理論物理学者・宇宙物理学者フリーマン・ダイソン博士(プリンストン高等研究所名誉教授)が出会い、お互いの研究テーマを紹介しあったところ、それぞれの分野で取り組んでいる内容を数式化したものがぴったりと一致することが判った。
すなわち、ヒュー・モンゴメリ博士が示したものはリーマン以後数多く見出されてきている、ゼータ関数のゼロ点の間隔を数式化したものであり、フリーマン・ダイソン博士が示したものは元素ウラン(U)の原子核の飛び飛びのエネルギー状態の間隔を示すものであった。このことが公表され、これまで疑問視されていた、素数と自然界の関係性についての関心が一気に高まり、1996年年にはアメリカ・シアトルで第1回世界リーマン予想会議が開催されるに至った。
ド・ブランジェ博士の抱いていた素数とミクロ世界にはつながりがあるという考え方の正しさが証明された形になった。ただ、リーマン予想そのものはまだ解決していない。
番組では、ド・ブランジェ博士はこれまでに3度リーマン予想を証明したと発表したものの、これらはその後証明が不完全であることがわかり、オオカミ少年になっていると紹介しているが、博士は全くこれを気にしている様子はなく、4度目の挑戦をしている姿を映している。
ある日の二人だけの食事の時に、博士が夫人に「(君は)いつだって疑うんだ・・・」とつぶやき、夫人が「時には信じているけど・・・」、「分からないわ・・・」と答える場面を紹介している。私はこの場面がとても好きだ。こうした家庭内のやりとりが、ド・ブランジェ博士の精神を健全に保ち、過去の多くの天才数学者が辿った道を歩ませていない理由なのだろうと思える。
番組は4回目のリーマン予想への挑戦論文を書きあげ、博士が口笛を吹きながら歩く姿を紹介し、これが正しいかどうか2年後に判る・・・として終わる。
前述のように、最近の情報として、昨年英国エディンバラ大学の名誉教授マイケル・アティヤ博士(1929.4.22~2019.1.11 英国・数学者、発表当時89歳)が2018年9月24日に発表した論文で、リーマン予想を証明したと伝えられているが、このことは同時に、ド・ブランジェ博士の4回目の挑戦もまた失敗であったことを物語っている。
マイケル・アティヤ氏は、リーマン予想の証明を発表する際に次のように語ったとされている。「ある物理定数を数学的に導出する過程で、リーマン予想を背理法を使って証明できた」。
博士の証明が正しいものかどうか、今後1年半後に判明することになるが、証明が正しいと認められたとしたらその時何がおきるのだろうか。多くの天才数学者が夢見た宇宙の大法則、根本原理が導かれることになるのだろうか。とても楽しみである。
小学生のころ、親から「学習百科」という名前だったと思うが、主要教科に関するあれこれが書かれた分厚い本を買ってもらって隅から隅まで熱心に読んだ記憶がある。その中の算数の部分に、自然数、素数といった言葉のほかに、2、3、4、5、などの数で割り切れる大きな自然数の見分け方といったことや、魔方陣の作り方が解説されていて興味深く読んだ。3で割り切れる数、すなわち3の倍数の見分け方は、もちろんご存知の方も多いことと思うが、各桁の数字を加えてその合計が3の倍数になれば、元の大きな数も3で割り切れるというものであり、子ども心にとても感心した。たとえば、
12345という数はは各桁の合計が1+2+3+4+5=15で3の倍数なので、12345÷3=4115と割り切れるが、23456の場合は、2+3+4+5+6=20なので、23456÷3=7818・・・2と割り切れず、3の倍数ではないといったぐあいである。
もう一つの、魔方陣というのは3x3、4x4,5x5・・・のマス目にそれぞれ1~9、1~16、1~25・・・までのすべての数字を入れて、タテ・ヨコ対角の数字の合計がどこも同じ値になるように配置したもので、自分で考えて作ろうとすると、なかなかむつかしいのだが、本に書かれている方法だと3x3や5x5などの奇数x奇数のマス目の場合は簡単に作れてしまうので大いに感心したのであった。
奇数x奇数のマス目の魔方陣の作り方については、ご存知の方も多いと思うが、次のように書かれていたことを覚えている。解法は、すべて共通しているが、3x3のマス目の場合で言うと、次の図の右側のように、中央の行と列をひとマスだけ外にはみ出させてできるひし形のマス目に、一番上から左下(右下でもいいが)に向かって1から順に3まで数字を置いてゆき、4は1の右下(左下)に置いてまた同じように6までを置く、7から9までも同様にしてマス目を埋め終わったら、外にはみ出している数字を、3x3のマス目内に戻す作業をする。その時のルールは矢印で示したように上下左右に移動させるが、一番遠い位置に戻すのである。
5x5のマス目の場合でも、ルールは全く同様なので確認していただければと思う。ただし、はみ出させるマス目の数は変化する。

3X3マス目の魔方陣の答え(左)と作り方(右)、タテ・ヨコ対角の数字の合計はすべて15になる

5X5マス目の魔方陣の答えの1例(左)と作り方(右)、タテ・ヨコ対角の数字の合計はすべて65になる
3x3のマス目の魔方陣は上下・左右の対称的配置は除くと、答は上記の配列だけである。一方、5x5のマス目の魔方陣については答は非常に多く、2億7530万5224通りあるとされている。上記解法で得られるものは、その1例に過ぎない。
4x4のマス目の魔方陣についての解法は出ていなかったように思うが、正確な記述についてはもう忘れてしまった。この4x4のマス目の魔方陣の答えは880通りあるとされているが、答えの一例は次のようなものである。

4X4マス目の魔方陣の答えの1例、タテ・ヨコ対角の数字の合計はすべて34になる
7x7のマス目の場合の解法も基本的に同じであるが。外にはみ出ている数字を戻す場合に、一番遠い位置という考えはできなくなるので、下図のように同じ色で示した2つの数字はそのまま一緒に同じ色の場所へ上下左右に移動させることで成立する。

7X7のマス目の魔方陣の答えの1例(左)と作り方(右)、タテ・ヨコ対角の数字の合計はすべて175になる
魔方陣に関する情報を検索していくと、更に大きなマス目の魔方陣や複雑なものも見られるが、この話題はこれくらいにしておく。
上記のマス目の問題は、自然数nの2乗に関する話ということもできるのであるが、これについてもう一つ興味深い話題がある。これは、知人の書いた「Why? 数の不思議あそび」(北川恵司著 2007年サイエンステイスト発行)で紹介されているものであるが、自然数nの2乗の数が見せるちょっと不思議な話題である。
10の2乗=100、11の2乗=121、12の2乗=144 といっても何の不思議もないが、これらの右辺の合計を見ると、100+121+144=365となり、どこかで見た数字になる。そう、1年の日数と一致している。話はこれだけで終わらない、続く13の2乗=169、14の2乗=196を見ると、169+196=365と再び365が登場する。これは何故か。もちろん数字の世界と、地球が太陽の周りを公転する周期と自転周期の比である1年の日数との間に関係などあるはずもなく、偶然の一致ということになろうが、数字の世界と自然界のもつ数値との関係を感じさせるということでちょっとした不思議である。
話は少し飛ぶが、数字と自然・宇宙との間にはなにか特別な関係が存在しているのではないだろうかという問題を考えた数学者は数多くいて、その究極が今からちょうど160年前に提出され、未だに解かれていないという数学史上最大の難問「リーマン予想」ということになる。
昨年2018年9月に、1859年に提出されたこのリーマン予想の証明が行われたとの報道がなされたが、数学の証明が正式に認められるまでには、2年間をかけての検証が必要とされているから、現時点ではまだ何とも言えない。
1,2,3,4,5,6,7,8,9,10・・・と続く自然数。その中には素数が含まれている。素数という数は1またはそれ自身以外に約数を持たない自然数ということになるが、2,3,5,7,11,13,17・・・という小学校で学ぶ数列である。この素数の謎を解明しようとした何人もの天才数学者の取り組みの中から生まれてきたのが、この「リーマン予想」だったということもできる。
もうずいぶん前にNHKのTV番組で素数問題に取り組む数学者をとりあげたことがあった。とても興味深い内容であったので、今もその放送を録画したディスクを大切に持っている。放送は2回、別々の番組として行われたが、内容はほぼ同じであった。探し出してみると「魔性の難問~リーマン予想・天才たちの戦い~」、「素数の魔力に囚われた人々~リーマン予想・天才たちの150年の闘い」というタイトルでそれぞれ、2009.11.15日と2009.11.21日に放送されたものの録画であった。
この放送はご覧になった方もおられることと思うが、次のような内容であった(今はYouTube で見ることができる)。
2,3,5,7,11,13,17・・と無限に続く素数には一見何の規則もなくランダムに出現しているように思える。素数であることを確認しながら、ずっと自然数を追っていくと次々と素数が見つかる場所があるかと思うと、しばらくは全く素数が現れない場所もあって、規則性などまったくないように思える。
しかし、この素数にはなにか宇宙の秘密が隠されているのではと直感的に感じた数学者もいて、根気よく素数を調べていった。その一人が、1700年代のスイス人の天才数学者・天文学者と言われているオイラー(1707.4.15~1783.9.18)であった。
彼は素数だけを用いた次のような数式(オイラー積)を考えてみた。するとその結果は収束して円周率π(パイ)の2乗を6で割った数字になることを見出した。このことからやはり素数にはなにか大自然とのつながりのある秘密が隠されているのではないかとの確信を深めていったが、当時はそれ以上進むことはなかった。

オイラーの肖像(ウィキペディアから)
次に番組で紹介されているのは、やはり天才数学者・天文学者・物理学者といわれたドイツ人ガウス(1777.4.30~1855.2.23)である。彼は15歳の頃、毎日1000個の自然数を検証することを自らに課し、その中にいくつの素数が含まれているかを数えたとされているが、その結果300万までの自然数のなかの素数を確認したとされている。

ガウスの肖像(ウィキペディアから)
一方、彼が素数の秘密に迫るために採ったアプローチは、自然対数表を用いるもので、見つかった素数Pをその素数の自然対数で割り答えQを求め、これをPが何番目の素数であるかを示すRと比較していった。素数Pが小さい間はQとRは一致せず、例えば素数9227に対するQ=1010、R=1144という具合であったが、次第に大きい素数になっていくにしたがって、素数262069の場合には、Q=21005、R=22992と、次第に両者の誤差が小さくなり、最終的にはQ=Rに収束するという発見をする。
このことは、素数が自然対数の底であるe(ネイピア数、=2.7182818284・・・)という、自然界でπ(パイ)と並んで最も重要な定数と関係していることが示された。
ガウスから約50年後に登場するのが、リーマン予想を提出したドイツ人の数学者リーマン(1826.9.17~1866.7.20)その人である。彼はオイラーやガウスの採ったアプローチに不満があったとされ、もっと数学的に厳密な方法で素数の並びに意味があるかどうかを調べようとして、オイラーが用いた式を少し変えた式リーマンゼータ関数というものを考案した。次のようなものである。

リーマンゼータ関数
この関数がゼロになる点、すなわち「ゼロ点」を先ず4つほど求めてみたところ、予想外の結果が得られた。4個のゼロ点は一直線上に並んでいた。

リーマンの肖像(ウィキペディアから)
TV放送では特に触れられていなかったが、この関数の変数は複素数で、ゼータ関数がゼロになる位置=ゼロ点は複素平面上の直線上に並んでいるということになる。
この結果を見て、リーマンはこのあと何人もの天才数学者の人生を翻弄することになる「リーマン予想」を提出することになる。それは次のようである。
リーマン予想:「ゼータ関数の非自明なゼロ点はすべて一直線上に並ぶはずだ」
ここで、非自明という言葉が使われているのは、自明なゼロ点というものも存在するからであるが、ここではこれ以上は触れない。
リーマンは、このリーマンゼータ関数のゼロ点という概念を素数の問題に取り込むことによって、「素数の並びには意味があるか」という漠然とした問題を素数だけからなる「ゼータ関数のゼロ点は直線上にだけ現れるか」という数学的な問題に置き換えることに成功した。
番組ではこのあと1950年代に、リーマン予想を証明しようと取り組んだ天才数学者を紹介していくが、かれらは次々と挫折し、その人生を狂わせていく。この挑戦者とは次のような人々である。
・ゴッドフレイ・ハーディー(1877.2.7~1947.12.1 英国・数学者)
・ジョン・リトルウッド(1885.6.9~1977.9.6 英国・数学者)
・ジョン・ナッシュ(1928.6.13~2015.5.23 アメリカ・数学者)
・アラン・チューリング(1912.6.23~1954.6.7 英国・数学者、論理学者、暗号解読者、コンピュータ学者)
3人目のジョン・ナッシュ博士は、1994年のノーベル経済学賞を受賞しているが、リーマン予想に取り組む中で、精神を病んでいく物語は、「ビューティフル・マインド」という映画に描かれたという。後年、ナッシュ博士は「数学的に考えるということは、心の内面に向き合うことであり、ある時には論理的にあるときは非論理的に考える必要があり、そうして心を病んでいった。」と振り返っている。
リーマン予想に取り組んだ数学者の多くは、自らも素数と自然界のつながりを信じ、これを証明しようとした。しかし、4人目の第二次大戦中にナチスドイツのエニグマ暗号を解読したことで知られるチューリング博士の場合は違っていた。彼は、素数の並びに意味があるとは信じておらず、ゼータ関数の4個のゼロ点が乗っている直線上以外の場所にあるセロ点をコンピュータを駆使してしらみつぶしに探していった。しかし、3カ月かけて1000個以上のゼロ点を見つけたものの、これらはすべて直線上にあり、直線の周辺にはまったく見つからなかった。さらにその後、チューリング博士は謎の死を遂げるという不幸に見舞われる。
仮に1個でも直線から外れた場所にゼロ点を見つけることができれば、リーマン予想はその意味を一気に失うことになったのであるが・・・。
このように不幸な出来事が続いた結果、リーマン予想に取り組むこと、あるいは取り組んでいるということを知られることは数学会のタブーのようになっていく。
放送で、その挑戦者の最後の一人として紹介されているのが、すでに数学の分野で多くの業績を挙げてきているフランス人数学者のルイ・ド・ブランジェ博士(放送当時77歳、1932.8.21~)であった。博士もまた素数と自然界との間の強い関係を信じ、独自の見解を持ち、素数を研究していた。それは素数は原子や素粒子などのミクロの世界とつながっているはずだというものであった。

ド・ブランジェ博士(ウィキペディアから)
この素数とミクロの世界とのつながりは、その後劇的なかたちで展開を見せる。舞台はヨーロッパからアメリカに飛ぶが、プリンストン高等研究所のお茶の時間に数学者ヒュー・モンゴメリ博士(ミシガン大学教授)と理論物理学者・宇宙物理学者フリーマン・ダイソン博士(プリンストン高等研究所名誉教授)が出会い、お互いの研究テーマを紹介しあったところ、それぞれの分野で取り組んでいる内容を数式化したものがぴったりと一致することが判った。
すなわち、ヒュー・モンゴメリ博士が示したものはリーマン以後数多く見出されてきている、ゼータ関数のゼロ点の間隔を数式化したものであり、フリーマン・ダイソン博士が示したものは元素ウラン(U)の原子核の飛び飛びのエネルギー状態の間隔を示すものであった。このことが公表され、これまで疑問視されていた、素数と自然界の関係性についての関心が一気に高まり、1996年年にはアメリカ・シアトルで第1回世界リーマン予想会議が開催されるに至った。
ド・ブランジェ博士の抱いていた素数とミクロ世界にはつながりがあるという考え方の正しさが証明された形になった。ただ、リーマン予想そのものはまだ解決していない。
番組では、ド・ブランジェ博士はこれまでに3度リーマン予想を証明したと発表したものの、これらはその後証明が不完全であることがわかり、オオカミ少年になっていると紹介しているが、博士は全くこれを気にしている様子はなく、4度目の挑戦をしている姿を映している。
ある日の二人だけの食事の時に、博士が夫人に「(君は)いつだって疑うんだ・・・」とつぶやき、夫人が「時には信じているけど・・・」、「分からないわ・・・」と答える場面を紹介している。私はこの場面がとても好きだ。こうした家庭内のやりとりが、ド・ブランジェ博士の精神を健全に保ち、過去の多くの天才数学者が辿った道を歩ませていない理由なのだろうと思える。
番組は4回目のリーマン予想への挑戦論文を書きあげ、博士が口笛を吹きながら歩く姿を紹介し、これが正しいかどうか2年後に判る・・・として終わる。
前述のように、最近の情報として、昨年英国エディンバラ大学の名誉教授マイケル・アティヤ博士(1929.4.22~2019.1.11 英国・数学者、発表当時89歳)が2018年9月24日に発表した論文で、リーマン予想を証明したと伝えられているが、このことは同時に、ド・ブランジェ博士の4回目の挑戦もまた失敗であったことを物語っている。
マイケル・アティヤ氏は、リーマン予想の証明を発表する際に次のように語ったとされている。「ある物理定数を数学的に導出する過程で、リーマン予想を背理法を使って証明できた」。
博士の証明が正しいものかどうか、今後1年半後に判明することになるが、証明が正しいと認められたとしたらその時何がおきるのだろうか。多くの天才数学者が夢見た宇宙の大法則、根本原理が導かれることになるのだろうか。とても楽しみである。