図Ⅰの図形A及びB上に点ア～オが与えられている。A又はBを、一直線上を滑ることなく回転させたとき、その図形上の点が描く軌跡が図Ⅱのようになった。このときの点として最も妥当なのはどれか。
①ア②イ③ウ④エ⑤オ 円が転がるときの、円の中心の軌跡と、円周上の点の軌跡は、次のようになります。
扇形の場合は、次のようになります。
ポイントは、ここです。
そうすると、本問では、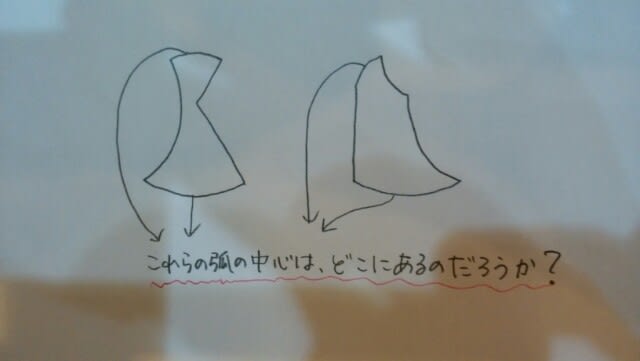
ということになりますね。
次に、
同じ記号どうしは、同じ軌跡になっています。○、△、×、□、☆で、元に戻っています。その間に、横一直線が2回出てきますね。（×と☆）そして、地面にくっつくときがあります。点アは、図形の内側にある点だから、地面にくっつくことはありません。
結局、○地面にくっつかない。○横一直線の軌跡が二つある。以上二つの理由で、正解は肢3です。要するに、図形Aと図形Bは、このような形に変形して考えれば速かったのです。
①ア②イ③ウ④エ⑤オ 円が転がるときの、円の中心の軌跡と、円周上の点の軌跡は、次のようになります。扇形の場合は、次のようになります。ポイントは、ここです。そうすると、本問では、ということになりますね。次に、同じ記号どうしは、同じ軌跡になっています。○、△、×、□、☆で、元に戻っています。その間に、横一直線が2回出てきますね。（×と☆）そして、地面にくっつくときがあります。点アは、図形の内側にある点だから、地面にくっつくことはありません。結局、○地面にくっつかない。○横一直線の軌跡が二つある。以上二つの理由で、正解は肢3です。要するに、図形Aと図形Bは、このような形に変形して考えれば速かったのです。