東京消防庁2類no18

4つの自然数A～Dがあり、この中から異なる2つの自然数を選び、その和をつくったところ、和は10、14、18、22、26の5通りであった。A＜B＜C＜Dのとき、Bの値として、最も妥当なのはどれか。 ① 6 ② 7 ③ 8 ④ 9 ⑤ 10　　　　　　　　　　　　　　　　　　　　次のような法則があります。本問は、4つの自然数ですが、5つでも6つでも、何個でも構わない。本問は、異なる2つの自然数の和ですが、3つの和でも4つの和でも、何個の和でも構わない。その和の、上位2つと下位2つは決まるが、それ以外は決まらない。本問は、A＋Bが一番小さく、A＋B＝10でA＋Cが2番目に小さく、A＋C＝14です。そして、C＋Dが一番大きく、C＋D＝26で、B＋Dが2番目に大きく、B＋D＝22です。すると、あとは18しか残っていないので、A＋DもB＋Cも18です。よって、正解は肢2です。
にほんブログ村

東京消防庁2類no17

ある商品100個を、仕入れ価格の3割増しで60個、1割増しで30個売り、10個を廃棄したときの利益は3300円であった。このとき、100個すべてを仕入れ価格の2割増しで売った場合の利益として、最も妥当なのはどれか。　　　　　①5400円②6000円③6400円④6800円⑤7200円よって、正解は肢2です。
にほんブログ村

東京消防庁2類no16

下の図のように正方形ABCDと△ABEの面積の比が4：3、△DEFの面積が1㎠であるとき、△CFBの面積として、最も妥当なのはどれか。正方形ABCDと△ABEの面積の比が4：3だから、正解は肢4です。
にほんブログ村

東京消防庁2類no15

0、1、2、3、4の5つの数字のうち、相異なる数字を用いてできる3桁の偶数の個数として、最も妥当なのはどれか。　　　　　　　　　　1. 30個　　2. 42個　　3. 48個　　4. 56個　　5. 60個普通というのは、それぞれの位の数が何通りあるかを調べて、掛け合わせるだけということです。並べるカードの中に0が入っていて、偶数が何個できるかという問題は、場合分けが必要なので、これら4パターンの中では、一番よく出題されます。このように、1の位が0のときと、1の位が0以外の偶数のときとで、百の位の場合の数が違ってくるからです。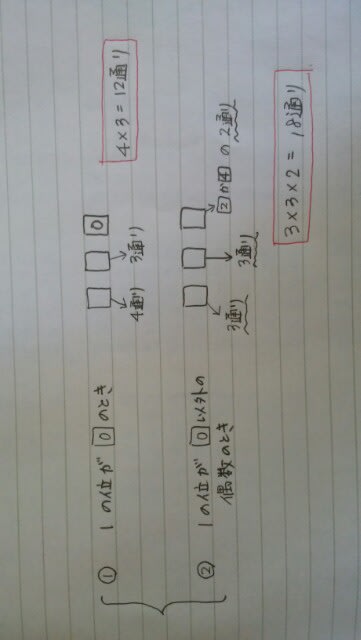よって、正解は肢1です。
にほんブログ村今日のオマケ蝉の群団

東京消防庁2類no14

下の図のような、長方形ABCDの紙をアとイの2通りの方法で折ってできる形として、最も妥当なのはどれか。ア　頂点Aと頂点Cが重なるように折った後、頂点Bと頂点Dが重なるように折る。　　　　イ　直線BDで折った後、頂点Aと頂点Cが重なるように折る。アについて。AとCが重なるように折ったときの折り目は、線分ACの垂直二等分線です。次に、BとDが重なるように折るので、線分BDの垂直二等分線を折り目として折ります。イについて。BDで折ると、次にAとCが重なるように折るので、テストでは、コンパス等は使用できませんので、だいたいの作図しかできませんが、アもイも、最後は四角形になるということさえ分かれば、面積は関係なしに、肢5しかありません。お手元の紙を自分で折って、確かめて下さい。