1と、その数自身しか約数を持たない自然数を「素数」といいます。ただし、1は素数から除外します（理由はかなり複雑）。 ゆえに、一番小さい素数は2ということになります。 また、2以外の偶数は、1と自分自身の他に、2という約数を持ってしまうので、素数ではなくなります。よって、2以外の素数は全て奇数です。 それでは問題です。 平成29年国家一般職（大卒）より。
数的推理というより、数学ですねぇ。まずは、－315を右辺に移項して、文字式を因数分解して、
この式から、（a＋b）も（a＋c）も、315の約数だなあと分かります。315の約数（正の約数）って何個あるのかなあ？と気になりますが、公式がありますね。これです。
よって、315は、正の約数を12個持ちます。
なので、（a＋b）（a＋c）＝315から先は、こうなります。
ただし、一番小さい素数が2で、その次に小さい素数が3ですから、（a＋b）は、5以上。2つは消去できます。
この次がハイライトです。 残った数は、全て奇数です。ということは、a＝2です。なぜだか分からない方は、もう一度この記事のはじめの方を読み直してみて下さいね。 素数は、ただ1つの例外を除いて、全て奇数です。（例外は2）よって、2つの素数の和は偶数になるはずです。なのに和が奇数なのだから、必ず2という素数が含まれているのです。a＝2と決まると、bもcも決まります。
3通りあります。正解は、肢2です。 ここをポチッとお願いします。→にほんブログ村 公務員系資格（公務員試験）
いろいろな平均の速さの問題を集めました。 Ⅰ 片道12kmの道のりを、行きは平均時速4kmで、帰りは平均時速6kmで歩いた。往復の平均時速を求めよ。（富山県教員採用試験）前回の公式より、
Ⅱ 太郎さんは、家から駅までの道のりを行きは時速6km、帰りは時速4kmで歩いた。往復の平均時速はどれだけか、正しいものを①～⑤から一つ選んで番号で答えなさい。①時速4.8km②時速5km③時速5.1km④時速5.2km⑤時速5.4km（京都市教員採用試験小学全科） Ⅰ の、行きと帰りの速さが逆になっているだけ。正解は肢①。 Ⅲ 12km離れたA町からB町へ行くのに、行きは平均4km/時で歩いた。往復の平均の速さを6km/時にしたい。帰りは平均でどのくらいの速さにすればよいか。（とある問題集）帰りの平均時速をxとすると、
正解は12km/時。公式を使うときは、距離（この場合は12km）は関係ないので、解くときには12は無視できるのでしたよね。 では、最後に、公式が使えない問題です。 Ⅳ A町からB町の間には上りの区間と平地の区間と下りの区間があり、上りの区間と平地の区間の距離は等しく、下りの区間は上りの区間の3倍の長さがある。いま、上りを3km/時、平地を6km/時、下りを9km/時の速さで行ったとき、平均の速さはいくらになるか。①5.0km/時②5.4km/時③5.6km/時④5.8km/時⑤6.0km/時（とある問題集） ある区間を往復している訳ではありませんし、全ての区間が同じ長さでもありませんので、きちんとやるしかありません。
距離は、l＋l＋3l＝5l（km）。かかった時間は、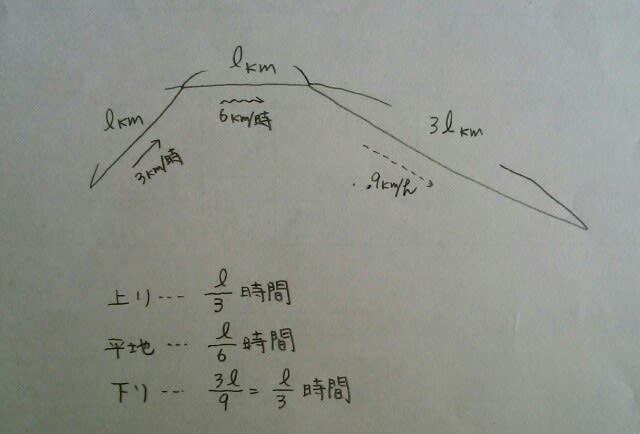
よって、
正解は、肢⑤です。ここをポチッとお願いします。→
「私はイチゴのケーキが欲しい」と、「私は、ケーキのイチゴが欲しい」は、どう違うのでしょう？ 前者は、ケーキを欲していますし、後者は、イチゴを欲しているのです。 イチゴのケーキは、あくまでも「ケーキ」であり、ケーキのイチゴは、「イチゴ」なのです。だから、「平均の速さ」を求めよといわれれば、我々は、「速さ」を求めなければいけないのです。 速さは、距離÷時間をして求めるのですね。Xkmの道のりを、行きは時速Akm、帰りは時速Bkmの速さで往復した。このときの平均の速さはいくらか。正しいものを1つ選び番号で答えなさい。ただし、単位はすべて［km／時］とする。
平均という修飾語につられて、肢5を選んではいけません。A＋Bは、距離ではありませんし、2は、時間ではありません。この人は、Xkmを往復したのだから、2Xkmという距離を進んだ訳です。では、往復にかかった時間はどれだけでしょうか？
だから、
正解は、肢4です。 実は、この式は、往復の平均の速さを求める有名な公式なのです。必ず覚えておきましょう。距離のXが、約分で消えましたね。つまり、この公式を使って平均の速さを求めるときは、距離はどうでも良いのです。まとめておきます。
また、誤解のないように言っておくと、これはあくまでも往復のことなので、
ほな、さいなら。あっ、ここをポチッとお願いします。→
あけましておめでとうございます。今年もよろしくお願いします。 ある製品が直線状のベルトコンベアにX（m）の間隔で配置され、一定の速さで運ばれている。図のように、検査員がベルトコンベアの横に立っていたところ、1分当たり3個の製品が通り過ぎていった。また、検査員がベルトコンベアの進行方向と同じ向きに、毎分20mの速さで移動していったところ、1分当たり2個の製品を追い越した。このとき、X（m）はいくらか。
①2m②4m③6m④8m⑤10m（平成29年地方上級より） 先に正解をいうと、20÷5＝4なので、肢②です。 まず本問は、ベルトコンベアで製品が流れてくるので、流水算かな、と思う人もいるかと思いますが、それは勘違いです。なぜなら、検査員は、ベルトコンベアに乗って移動する訳ではないからです。 ベルトコンベアに乗って移動する製品がA君、検査員がB君で、2人が同時にジョギングを始めたくらいの感じで本問をみて下さい。そうすると、こうなりますね。「検査員がベルトコンベアの横に立っていたところ、1分当たり3個の製品が通り過ぎていった。」ということは、
検査員は、1分当たり2個の製品を追い越した、ということは、
ところで、検査員は毎分20mの速さなのだから、
それにしても、毎分20mなどという速さで歩こうとすれば、あまりに遅すぎて、かなりストレス溜まりそうです。 時速にすると、1.2km／時。大人が普通に歩くと4km／時。小さな子供と手を繫いでゆ～くり歩くと2km／時。野球のピッチャーからホームベースまでが、確か18.44mだったと思うのですが、1分で20mというのは、実際に可能なのかどうか？とりあえず、ここをポチッとお願いします。→