前回のT検定は、いわゆる通常の検定でした。
JASPの特徴は、最近、話題の”ベイズ推定のT検定”が出来ることかも知れません。
そこで、
JASPの特徴でもある”ベイズ推定のT検定”をご紹介しましょう。
JASPの特徴は、最近、話題の”ベイズ推定のT検定”が出来ることかも知れません。
そこで、
JASPの特徴でもある”ベイズ推定のT検定”をご紹介しましょう。
前回と同じように、「T-Test」アイコンから、
“BayesianIndependent Samples T-Test”を選択して下さい。
変数の選択は、前回と同じ”GTP”と”Group-1"とします。
図1 変数と検定項目の選択
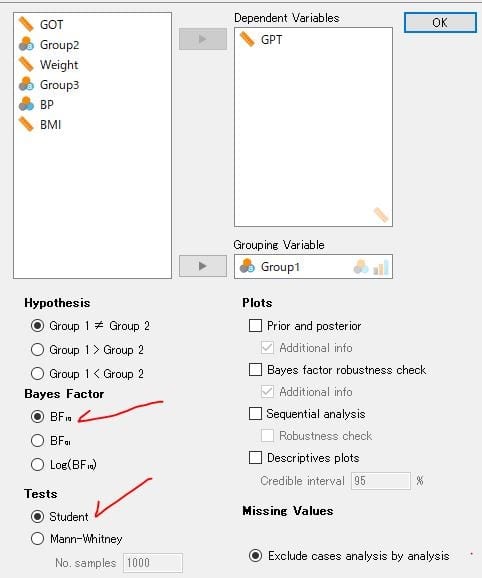
注釈;
*****
Dependent Variables(従属変数)→GPT
Grouping Variable(群分変数)→Group1
Hypothesis(仮説)→Group 1≠Group 2
Bayes Factor(ベイズファクター)→BF10
Test(検定)→Student
*****
ここで、
”ベイジアン t 検定”が”通常のt検定”と違うところは、平均値差の効果量が「0」と言う帰無仮説を立てます。
従って、対立仮説は「0」でないことであり、その判定は「ベイズファク ター」(仮説検定の証拠となる指標)で決まります。
通常、
”ベイジアン t 検定”(ベイズファク ター)で、
● BF10の大きさは対立仮説を採用する(2群の平均値に差がある)判断基準となる。
● BF01の大きさは帰無仮説を採用する(2群の平均値に差はない)判断基準となる。
”ベイジアン t 検定”が”通常のt検定”と違うところは、平均値差の効果量が「0」と言う帰無仮説を立てます。
従って、対立仮説は「0」でないことであり、その判定は「ベイズファク ター」(仮説検定の証拠となる指標)で決まります。
通常、
”ベイジアン t 検定”(ベイズファク ター)で、
● BF10の大きさは対立仮説を採用する(2群の平均値に差がある)判断基準となる。
● BF01の大きさは帰無仮説を採用する(2群の平均値に差はない)判断基準となる。
・・このことを意味し、表1の基準で判断が出来ます。
表1Bayes(BF値)のFactor基準
----------------------------
1- 3:乏しい
3- 10 :中程度
10-30:強い
30-100:とても強い
>100:非常に強い
----------------------------
1- 3:乏しい
3- 10 :中程度
10-30:強い
30-100:とても強い
>100:非常に強い
----------------------------
では、
例題(GPT)の結果をみてみましょう(図2)。
図2 GPTの”ベイジアンt検定”の結果
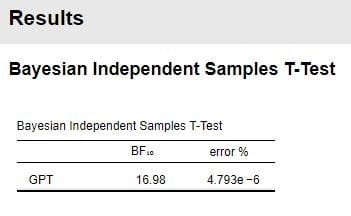
BF10 の値は「16.98」であり、表1から Factor の基準は「強い」と判断されます。
すなわち、
平均値差に関する効果量が「0」という帰無仮説を破棄し対立仮説(平均値に差があること)を採用することになります。
すなわち、
平均値差に関する効果量が「0」という帰無仮説を破棄し対立仮説(平均値に差があること)を採用することになります。
では、
図1において「BF01」を選択したときは、どうなるでしょうか。
図1において「BF01」を選択したときは、どうなるでしょうか。
「BF01=0.059」となり、「0」に近く帰無仮説(平均値に差がないこと)の採用は極めてと乏しいと言えます。
それでは、
「GOT」ではどうでしょうか。GOTの BF値は次のようになりました。
「GOT」ではどうでしょうか。GOTの BF値は次のようになりました。
BF10=0.310
BF01=3.221
BF01=3.221
よって、帰無仮説(平均値に差がないこと)を支持することが出来ます。
なお、Log(BF10)はBF10の自然対数変換値です。
次回に続く!
情報統計研究所はここから









