二元配置分散分析をやってみましょう。
例題は、
「統計学入門、第4章 多標本のデータ処理」(杉本典夫 先生)から引用させて頂きます。
下記URLにアクセスして、
http://www.snap-tck.com/room04/c01/stat/stat04/stat0403.html
「統計学入門、第4章 多標本のデータ処理」(杉本典夫 先生)から引用させて頂きます。
下記URLにアクセスして、
http://www.snap-tck.com/room04/c01/stat/stat04/stat0403.html
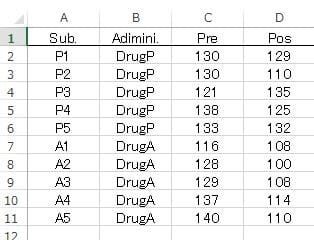
・・・「表4.3.4 薬剤投与前後の収縮期血圧」 のデータを図1のようにExcelに入力し編集し、例えば、
「TwoWayRep.csv」として保存して下さい。
「TwoWayRep.csv」として保存して下さい。
図1 Excel データの入力形式
*****
JASP の起動→「TwoWayRep.csv」の読込
↓
ANOVA→Repeated Measures ANOVA
↓
図2 変数の選択(変数PreとPosの名義を Scaleに変更)
JASP の起動→「TwoWayRep.csv」の読込
↓
ANOVA→Repeated Measures ANOVA
↓
図2 変数の選択(変数PreとPosの名義を Scaleに変更)

Between Subject Factors→Admini
↓
図3 Repeated Measures ANOVA の結果
↓
図3 Repeated Measures ANOVA の結果

↓
図4 TwoWay ANOVAのグラフ作成

結果の解釈などは、
「統計学入門、第4章 多標本のデータ処理」の「表4.3.5 繰り返し測定データの分散分析表」などを参考に理解して欲しいと思います。
なお、
ベイズの方法は、
「Bayesian Repeated Measures ANOVA」
↓
図5 BRM ANOVA の結果
ベイズの方法は、
「Bayesian Repeated Measures ANOVA」
↓
図5 BRM ANOVA の結果

ところで、
「表4.3.5 繰り返し測定データの分散分析表」の「SUB:被験者」の統計量はJASPで出力されません。
そこで、
「表4.3.5 繰り返し測定データの分散分析表」の「SUB:被験者」の統計量はJASPで出力されません。
そこで、
図2の「Between Subject Effect」から、
*****
Sum of Squares の合計=432.4+501.6=934
df の合計=1+8=9
Mean Square の計算=934/9=103.78
F値の計算=103.78/被験者残差Ms=1.69997
P値の計算=F.DISTRT(1.999967,9,8)=0.2332
Sum of Squares の合計=432.4+501.6=934
df の合計=1+8=9
Mean Square の計算=934/9=103.78
F値の計算=103.78/被験者残差Ms=1.69997
P値の計算=F.DISTRT(1.999967,9,8)=0.2332
*****
・・・となります。
さて、
ベイズを簡単に要約すると、
*****
何らかの事前情報(分布)のあるデータから事後の分布(確率)を予想すること。
*****
・・・と言えるでしょうか。
ベイズを簡単に要約すると、
*****
何らかの事前情報(分布)のあるデータから事後の分布(確率)を予想すること。
*****
・・・と言えるでしょうか。
JASPでは事前情報のない無情報事前分布を一様分布として扱っています。
色々と議論のあるところと思いますが、このブログではJASPのマニュアルに従ってご紹介したいと思います。
色々と議論のあるところと思いますが、このブログではJASPのマニュアルに従ってご紹介したいと思います。
次回に続く!
情報統計研究所はここから。









