Gooブログ「新・医学と統計」では、近年、注目されている「フリー統計解析ソフト:JASP」でのベイズ統計を簡単な例題で、その方法をご紹介しています。「統計=難しい」と敬遠される向きもありますが、まずは職場などで統計を取りれたプレゼンをして欲しいと思っています。
このブログでは、
統計学よりも統計的方法のご紹介を旨としていますが、今回の新・医学と統計(18)の内容について貴重なコメントを頂きましたのでご参考になさて下さい。
杉本典夫先生のコメント1(原文):
<<<
Fisherの正確検定とχ2乗検定の関係について少しコメントします。
これら2種類の手法はよく混同されて用いられていますが、実は検定している評価指標が少し異なります。
Fisher の正確検定は 2群の出現率の差 (リスク差) の検定であり、それが 0かどうかを検定します。
図2「新・医学と統計(18)」の「Contingency Tables」で言えば、
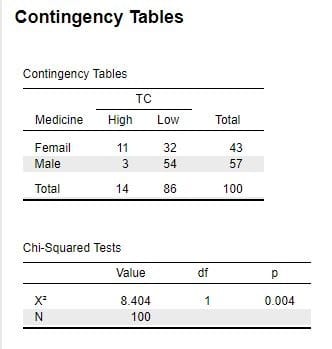
FemaleのTC-High(またはTC-Low)の出現率と、MaleのTC-High(またはTC-Low)の出現率の差が 0かどうかを検定するわけです。そして計算の前提として、
Female群の例数と Male群の例数には誤差がなく、TC のHighと Lowの例数だけに誤差があると仮定していて、その仮定から理論的に導かれる超幾何分布を利用して計算します。
このようなデータは、
Female群の例数と Male群の例数をあらかじめ指定し、TC のHighと Low の例数を観測した「前向き研究」から得られたものでそれに対してχ2乗検定は、2種類の分類項目間の関連性(独立性)の検定であり、名義尺度同士の相関係数に相当する連関係数(Cramerの連関係数)が 0かどうかを検定します。
そして計算の前提として、
全体の例数には誤差がなく、Femaleと Maleの例数にも、TC-HighとTC-Low の例数にも誤差があると仮定していて、その仮定から近似的に導かれるχ2乗分布を利用して計算します。
全体の例数をあらかじめ指定し、TC のHighと Low の例数を観測した「横断的研究」から得られたものです。









