新・医学と統計(21)

前回「新・医学と統計(18)」の分割表（Frequency.csv）を用いて「Baysian Contingency Tables」をやってみましょう。

 

JASP→Frequencies→Bayesian Contingency Tables
↓
新・医学と統計(18)の図１と同じ要領で変数を選択
↓
図１　検定方法の選択　

 

 

 

Statistics のデフォルトは、
◎ Indep.multinominal row fixed（行の固定）

 

となっています。

 

Additional Statistics☑ Log odds ratio (2×2 only)をチェックしてみましょう。
↓
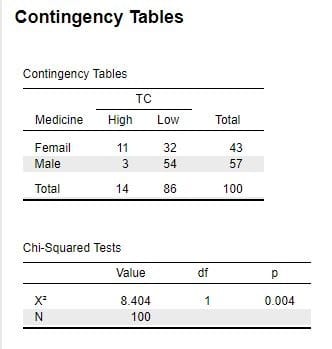
図２　出力結果　

 

 

***
医学研究などにおいて分割表の形式は研究（実験）方法によって変わってくるものです。

通常、次のような場合が考えられます。
・度数が固定されていない。
・総度数が決まっている。
・行の度数が決まっている。
・列の度数が決まっている。

 

これらは、医学実験などによって決まっていたりします。
例えば、
被験者数などが事前に決まっている場合などでは総数固定になります。

 

分割表のベイズ分析のために開発された主に次の４つのプラン（スキーム）を検討することが出来ます。
Poisson（ポアソン）、 joint multinomial（結合又は同時多項）、independent multinomial（独立多項）、hypergeometric（超幾何）

 

Poisson（ポアソン）：
各セル数はすべてランダムでポアソン分布に従うものです。

 

joint multinomial（結合多項）：
ポアソンと同じですが総数が固定されています。

 

independent multinomial（独立多項）：
これは行と列の合計が決まっているもので実験心理学でよく用いられています。
JASPでは default となっています。

 

hypergeometric（超幾何）：
これは行と列の両方の合計が固定された Fisher's test の計算と考えて下さい。

Fisher's test の計算は「すぐに役立つ統計のコツ」（オーム社刊）の 44ページに Excelでの計算法をご紹介しています。

 

文献：
Jamil, T., Ly, A/, & Wagenmakers, E-J.(2017). Default "Gunel and Dickey" Bayes factors for contingency tables.
 Manuscript submitted for publication (Preprint).

 

 

次回に続く！

 

情報統計研究所をご気軽にご利用くださいませ。

 

情報統計研究所刊：「すぐに役立つ統計のコツ」立読み
↓
https://e-hon.cloudpages.jp/viewer/asp/9784_274_218163

 

 

新・医学と統計(20)

Gooブログ「新・医学と統計」でご紹介している「フリー統計解析ソフト：JASP」は、ある程度の統計学の知識が必要かと思います。また、

JASPが注目される理由の１つに比較的簡単にベイズ統計を経験できるところかも知れません。
ベイズ統計を経験するつもりで、JASPをお楽しみ下さい。
なお、
杉本典夫先生には「Gooブログ：新・医学と統計」を補完する貴重なコメントでを賜り心より感謝申し上げます。

前回に引き続き、
杉本典夫先生のコメントをご紹介します。

 

杉本典夫先生のコメント1（原文）：
<<<
Fisherの正確検定とχ2乗検定の関係と同様のことが、回帰係数の検定と相関係数の検定の関にも存在します。
回帰分析は、
説明変数xの値には誤差がなく、目的変数yの値にだけ誤差があるという前提で理論を組み立てています。そのため回帰分析を適用するデータは、原則として前向き研究から得られたデータです。
そして、
標本回帰係数は自由度(n-2)の t分布をするため、この分布を利用して回帰係数が 0かどうかの検定を行います。
それに対して相関分析は、
両方のデータに誤差があるという前提で理論を組み立てています。そのため相関分析を適用するデータは、原則として横断的研究から得られたデータです。
そして、
標本相関係数は 2次元 t分布をするため、厳密な検定をするのは非常に面倒です。
そこでFisherは、
母相関係数=0 の時、標本相関係数の分布が自由度(n-2)の t分布で近似できることを証明し、相関係数の検定に回帰係数の検定と同じ計算式を用いることを提唱しました。
ただし、
母相関係数≠0 の時は近似が悪いので、z変換という特殊な変換をして正規分布で近似し、それを母相関係数の区間推定に利用することにしました。
これと同様のことを、
Fisherの弟子のYates がχ2乗検定に応用しました。
連続修正を加えたχ2乗分布によって超幾何分布を近似し、出現率の差の検定を、計算方法が簡単なχ2乗検定によっても行えるようにしたのです。
これが、
連続修正(Yatesの補正)付きχ2乗検定です。
ただし
連続修正付きχ2乗検定は連関係数の検定としては誤差が大きいので、連関係数の検定にはオリジナルのχ2乗検定を用いるのが普通です。
連続修正の原理については、

僕のサイトの次のページをご覧ください。
www.snap-tck.com/room04/c01/stat/stat03/stat0302_2.html

>>>

 

次回は Baysian Contingency Tables の予定です。

 

情報統計研究所をご気軽にご利用くださいませ。

 

 

新・医学と統計(19)

Gooブログ「新・医学と統計」では、近年、注目されている「フリー統計解析ソフト：JASP」でのベイズ統計を簡単な例題で、その方法をご紹介しています。「統計＝難しい」と敬遠される向きもありますが、まずは職場などで統計を取りれたプレゼンをして欲しいと思っています。
このブログでは、
統計学よりも統計的方法のご紹介を旨としていますが、今回の新・医学と統計（18）の内容について貴重なコメントを頂きましたのでご参考になさて下さい。

杉本典夫先生のコメント1（原文）：
<<<
Fisherの正確検定とχ2乗検定の関係について少しコメントします。
これら2種類の手法はよく混同されて用いられていますが、実は検定している評価指標が少し異なります。
Fisher の正確検定は 2群の出現率の差 (リスク差) の検定であり、それが 0かどうかを検定します。
図2「新・医学と統計(18)」の「Contingency Tables」で言えば、

FemaleのTC-High(またはTC-Low)の出現率と、MaleのTC-High(またはTC-Low)の出現率の差が 0かどうかを検定するわけです。そして計算の前提として、
Female群の例数と Male群の例数には誤差がなく、TC のHighと Lowの例数だけに誤差があると仮定していて、その仮定から理論的に導かれる超幾何分布を利用して計算します。
このようなデータは、
Female群の例数と Male群の例数をあらかじめ指定し、TC のHighと Low の例数を観測した「前向き研究」から得られたものでそれに対してχ2乗検定は、2種類の分類項目間の関連性(独立性)の検定であり、名義尺度同士の相関係数に相当する連関係数(Cramerの連関係数)が 0かどうかを検定します。

そして計算の前提として、
全体の例数には誤差がなく、Femaleと Maleの例数にも、TC-HighとTC-Low の例数にも誤差があると仮定していて、その仮定から近似的に導かれるχ2乗分布を利用して計算します。

このようなデータは、
全体の例数をあらかじめ指定し、TC のHighと Low の例数を観測した「横断的研究」から得られたものです。

このように2種類の手法は評価指標が異なり、計算の前提が異なり、利用する分布が異なるので、当然、結果も異なります。

>>>

杉本典夫先生のコメント2 は次回に！