ガラスを構造面で見れば非晶質、原子配列に(長距離)規則性のないランダム配列を持つ物質ということになる。
物質は、気体、液体、固体に分けることができるが、気体、液体中の原子・分子の配列はランダムであり、規則的な原子配列は固体の特徴である。
ガラスは固体でありながら、規則的な原子配列を持たず、液体状態の原子配列を保ったまま固体化したものといえ、規則配列を持つ結晶の対極にあるといえる。
さて今回は、ちょっと横道にそれるが、そのガラスと結晶の間に見つかったもう一つの個体、1984年にイスラエルの金属学者ダニエル・シェヒトマン(Daniel Shechtman, 1941.1.24- )によって発見された準結晶についてのお話。
規則配列は、固体の特徴と書いたが、実際には液体の中にも、固体結晶に匹敵するような高度の規則配列を持つ物質があり、液晶と呼ばれている。
液晶には、その規則性の程度に応じて、ネマティック液晶、スメクティック液晶、コレステリック液晶の3種があるが、現在我々の周辺に溢れている液晶ディスプレイ(LCD)はこのうちの、ネマティック液晶が持つ規則的な配列のある性質を利用したものである。
液晶は、準結晶よりもずいぶん早く、1888年にオーストリアの植物学者フリードリッヒ・ライニッツァ-(Friedrich Reinitzer, 1857.2.25-1927.2.16)によって発見されていたが、実用的な開発が進められたのは第二次大戦後になってからであった。
そして、この液晶研究関連では、1991年のノーベル物理学賞が、フランスのピエール=ジル・ド・ジェンヌ(Pierre-Gilles de Gennes, 1932.10.24-2007.5.18 )に授与された。
その理由は「単純な系の秩序現象を研究するために開発された手法が、より複雑な物質、特に液晶や高分子の研究にも一般化され得ることの発見」とされている。
本題の準結晶に戻るが、先ずペンローズにより見出された「ペンローズタイル」について触れておく必要がある。
少し前(2018.6.8 公開)に、エッシャーの版画を紹介し、その時に「滝」などの3次元の成立不能図形が、イギリスの数学者、宇宙物理学・理論物理学者ペンローズ(Sir Roger Penrose, 1931.8.8- )が発見した「ペンローズの三角形」をヒントにしたものであったことに触れた。
このとき示したエッシャーのもう一つの作品「メタモルフォーゼ」に代表される2次元の不思議なタイリングパターンについては、ペンローズが発見したもう一つの図形「ペンローズタイル」との関係があったとされている。
ペンローズは二次元平面を埋め尽くす5回対称図形を考案したが、それがこの「ペンローズタイル」である。
1種類の正多角形を用いて平面充填が可能になるのは、正三角形、正四角形(正方形)、正六角形の3種に限られ、正五角形は図のように、平面を埋め尽くすことができない。このことは、古くアルキメデスにより数学的に証明されている。
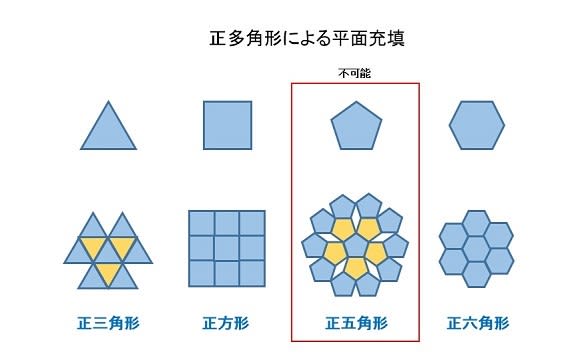
正多角形による平面充填
また、正三角形、正方形、正六角形で実現した平面充填パターンは、並進対称性、すなわち充填図形を一定の方向にずらした場合に、元の図形と一致する性質を持つ。
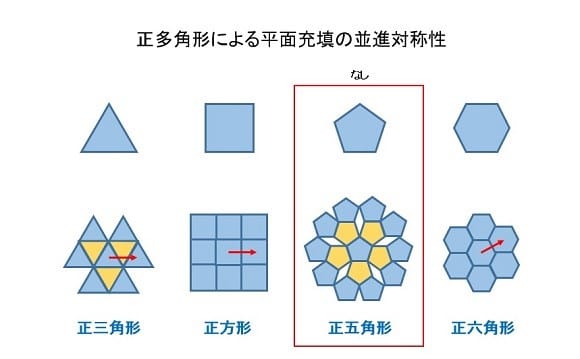
正多角形の充填図形が示す並進対称性
これらの図形にはもうひとつの対称性、回転対称性があり、正三角形、正方形、正六角形による充填図形には、図形面に垂直な軸の周りに、それぞれ120°、90°、60°回転させた場合に、元の図形と一致する性質をもち、それぞれ3回対称、4回対称、6回対称と呼ばれる。
ところで、正五角形はどうかというと、平面充填ができず、並進対称性はないが、次図のように配列させた正五角形は、5回対称性を持つことがわかる。

正多角形からなる充填図形が示す回転対称性
「ペンローズタイル」はこの5回対称性を持ち、平面充填が可能な図形を2種類の菱形を用いて実現したものである。

ペンローズタイルを構成する2種類の菱形
この鋭角が72°と36°の2種類の菱形からなるペンローズタイルのパーツを、図の矢印の色と方向が一致するように厳密につなぎ合わせるというルールで平面充填させたものがペンローズタイルと呼ばれているパターンである。
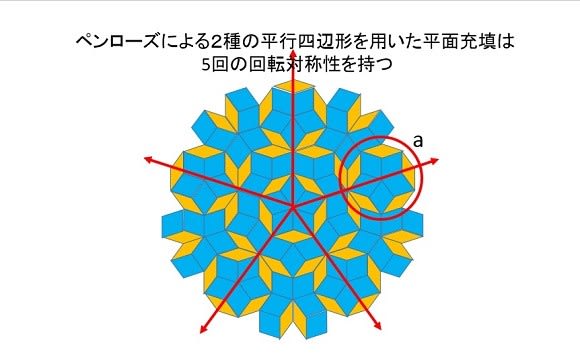
ペンローズタイル
この図から判るように、ペンローズタイルは5回対称性をもち、中心から外に向かって無限に広がるパターンであり、並進対称(周期)性は持たない。ただし、厳密な並進周期姓はないものの完全なランダム配列でもなく、周期構造に近い構造すなわち「準周期構造」を持っていることが明らかにされている。
前記の厳密なつなぎ合わせの条件をはずすと、この2種類の菱形を用いて平面充填をさせうる配置の組み合わせは、無限に存在する。たとえば、図中に「a」で示した正10角形は、中心軸の周りに回転させうるが、これにより、異なる配列パターンができる。同様の正10角形は、この図を外に向かって拡大していくと、その図形中に無数に存在していることから前記のことが理解される。
このペンローズパターンは、当初は単に興味深い平面充填パターンとして関心をもたれていただけであったが、後に発見された準結晶が、このペンローズパターンどおりの原子配置を持つことが判り、にわかに注目されるようになった。
準結晶は、液体状態から急冷したAlとMnの合金から発見された。初期のこの準結晶は不安定で、加熱するとより安定な結晶相が析出していたが、やがて安定な準結晶が続々と発見されている。
2011年には、最初にこの準結晶を発見したダニエル・シェヒトマンにノーベル化学賞が授与された。
ペンローズパターンは2次元の非周期性の平面充填構造であるが、実際の3次元準結晶ではどのような原子配列になっているのか興味あるところである。
シェヒトマンにより発見された準結晶の電子線回折図形は、結晶の回折図形のような回折スポットの集合であるにも関わらず、2回、3回の回転対称性に加え、結晶には存在しない5回対称性を示し、正20面体の持つ対称性を有していた。
その後に発見された準結晶Al-Ni-Co系などには、正10角柱と同じ対称性をもつ準結晶相も存在する。この準格子は2次元ペンローズパターンであり、この面が積層した構造をもつとされる。この場合、平面方向には準周期構造、これと垂直な軸方向には周期構造を有している。このほか、8角形相、12角形相の準結晶が見つかっている。
準結晶に特有の物性といったものはどうだろうか。金属元素から構成されたものとしては異常に高い電気抵抗があげられている。例えば、アルミニウム、銅、鉄は単体ではいずれも良導体であるが、これらからなる準結晶Al-Cu-Feでは電気抵抗が10万倍にも達し、周期構造の欠如が原因と考えられている。また、準結晶は、その非周期性のためへき開を形成し難く、このため比較的硬くて強靭である。それに、テフロン並みに低い表面エネルギーのものが見つかっていて、Al-Fe-Cu準結晶はフライパンのコーティング材として使用されているという。
これまで得られている準結晶は人工的に作られたものであるが、熱力学的に安定な平衡状態にあるとすれば、自然には存在しないものだろうかという疑問が沸く。
この点については、2016年に、宇宙からやってきた隕石中から準結晶が見つかったとの報告がされている。イタリア、フローレンス大学の地質学者Luca Bindi博士らのチームが極東ロシアのハトゥイルカ地方に5年前に落ちた隕石の破片の中に、数ミクロンの準結晶構造を見つけている。
この隕石の内部に準結晶構造が見つかったのは3度目のことであった。この準結晶もアルミニウム、銅、鉄の原子から構成されており、5回対称の構造を持っているとされる。
今年に入って、名古屋大学は2018年1月20日、豊田工業大学、東北大学、豊田理化学研究所との共同研究により、超伝導になる準結晶を世界に先駆けて発見したと発表した。この研究は、磁石や超伝導をもたらす「電子の長距離秩序」が準結晶では本質的に不在なのかを解明することを目的として行われ、Al、Zn、Mg の3元素を組み合わせ、高速急冷法により準結晶を合成し行われたものであった。
ペンローズは数学者であり、理論・宇宙物理学者でもある。米国の同じ理論・宇宙物理学者のリサ・ランドール(Lisa Randall、1962.6.18- )はペンローズタイプの準結晶の構造をとりあげて、その著書「ワープする宇宙・5次元時空の謎を解く」(原題 Warped Passages, 向山信治監訳 塩原通緒訳、2007年 NHK出版発行)の中で次のように述べている。
「余剰次元-(筆者注:われわれが存在している三次元空間とは別の次元のこと)-の痕跡が、あなたの台所にも隠れているかもしれない--と言ったら驚くだろうか。それは『準結晶』でコーティングした焦げつかないフライパンである。準結晶というのは不思議な構造で、その根本的な秩序は余剰次元でしか解明されない。ふつうの結晶は、原子や分子がきわめて対称的な格子状になって一定の基本配列で繰り返し並んでいる。三次元で結晶がどんな構造を形成するかはわかっているし、どんな並びがありうるかもわかっている。しかし準結晶における原子と分子の配列は、その並びのいずれとも合致しないのだ。
準結晶の並びの一例が、図2(筆者注:ペンローズタイルの図が示されている)である。ここには結晶に見られる厳密な規則性が欠けている。普通の結晶ならば、もっと方眼紙のマス目のようなものに見えるはずだ。この奇妙な物質の分子の並びを説明する最もエレガントな方法は、これを高次元の結晶構造の射影-三次元の影のようなもの-と見ることである。つまり、その並びは高次元空間での対称性をうちに秘めているのである。三次元においてはまったく不可解に見えた配列も、高次元世界においては秩序のとれた構造になる。準結晶でコーティングされたフライパンは、そのコーティングのなかの高次元結晶の射影と、もっとありふれた通常の三次元の食材との構造的な違いを利用しているわけだ。原子の配列が違うから、それぞれの原子が互いに結合することがない。これは余剰次元が実際に存在していて、いくつかの観測可能な物理現象を説明できることを強く示唆するものである。」
にわかに理解しがたい話であるが、どのように考えればいいのだろうか。数学者ペンローズが2次元平面における5回対称性を実現させるために考案したペンローズタイルは、準結晶の発見を通して、5次元空間との関連性を示し、宇宙物理学者ペンローズの元へと戻ってきた。あたかも、エッシャーのメタモルフォーゼの循環を見ている思いがする。
物質は、気体、液体、固体に分けることができるが、気体、液体中の原子・分子の配列はランダムであり、規則的な原子配列は固体の特徴である。
ガラスは固体でありながら、規則的な原子配列を持たず、液体状態の原子配列を保ったまま固体化したものといえ、規則配列を持つ結晶の対極にあるといえる。
さて今回は、ちょっと横道にそれるが、そのガラスと結晶の間に見つかったもう一つの個体、1984年にイスラエルの金属学者ダニエル・シェヒトマン(Daniel Shechtman, 1941.1.24- )によって発見された準結晶についてのお話。
規則配列は、固体の特徴と書いたが、実際には液体の中にも、固体結晶に匹敵するような高度の規則配列を持つ物質があり、液晶と呼ばれている。
液晶には、その規則性の程度に応じて、ネマティック液晶、スメクティック液晶、コレステリック液晶の3種があるが、現在我々の周辺に溢れている液晶ディスプレイ(LCD)はこのうちの、ネマティック液晶が持つ規則的な配列のある性質を利用したものである。
液晶は、準結晶よりもずいぶん早く、1888年にオーストリアの植物学者フリードリッヒ・ライニッツァ-(Friedrich Reinitzer, 1857.2.25-1927.2.16)によって発見されていたが、実用的な開発が進められたのは第二次大戦後になってからであった。
そして、この液晶研究関連では、1991年のノーベル物理学賞が、フランスのピエール=ジル・ド・ジェンヌ(Pierre-Gilles de Gennes, 1932.10.24-2007.5.18 )に授与された。
その理由は「単純な系の秩序現象を研究するために開発された手法が、より複雑な物質、特に液晶や高分子の研究にも一般化され得ることの発見」とされている。
本題の準結晶に戻るが、先ずペンローズにより見出された「ペンローズタイル」について触れておく必要がある。
少し前(2018.6.8 公開)に、エッシャーの版画を紹介し、その時に「滝」などの3次元の成立不能図形が、イギリスの数学者、宇宙物理学・理論物理学者ペンローズ(Sir Roger Penrose, 1931.8.8- )が発見した「ペンローズの三角形」をヒントにしたものであったことに触れた。
このとき示したエッシャーのもう一つの作品「メタモルフォーゼ」に代表される2次元の不思議なタイリングパターンについては、ペンローズが発見したもう一つの図形「ペンローズタイル」との関係があったとされている。
ペンローズは二次元平面を埋め尽くす5回対称図形を考案したが、それがこの「ペンローズタイル」である。
1種類の正多角形を用いて平面充填が可能になるのは、正三角形、正四角形(正方形)、正六角形の3種に限られ、正五角形は図のように、平面を埋め尽くすことができない。このことは、古くアルキメデスにより数学的に証明されている。

正多角形による平面充填
また、正三角形、正方形、正六角形で実現した平面充填パターンは、並進対称性、すなわち充填図形を一定の方向にずらした場合に、元の図形と一致する性質を持つ。

正多角形の充填図形が示す並進対称性
これらの図形にはもうひとつの対称性、回転対称性があり、正三角形、正方形、正六角形による充填図形には、図形面に垂直な軸の周りに、それぞれ120°、90°、60°回転させた場合に、元の図形と一致する性質をもち、それぞれ3回対称、4回対称、6回対称と呼ばれる。
ところで、正五角形はどうかというと、平面充填ができず、並進対称性はないが、次図のように配列させた正五角形は、5回対称性を持つことがわかる。

正多角形からなる充填図形が示す回転対称性
「ペンローズタイル」はこの5回対称性を持ち、平面充填が可能な図形を2種類の菱形を用いて実現したものである。

ペンローズタイルを構成する2種類の菱形
この鋭角が72°と36°の2種類の菱形からなるペンローズタイルのパーツを、図の矢印の色と方向が一致するように厳密につなぎ合わせるというルールで平面充填させたものがペンローズタイルと呼ばれているパターンである。

ペンローズタイル
この図から判るように、ペンローズタイルは5回対称性をもち、中心から外に向かって無限に広がるパターンであり、並進対称(周期)性は持たない。ただし、厳密な並進周期姓はないものの完全なランダム配列でもなく、周期構造に近い構造すなわち「準周期構造」を持っていることが明らかにされている。
前記の厳密なつなぎ合わせの条件をはずすと、この2種類の菱形を用いて平面充填をさせうる配置の組み合わせは、無限に存在する。たとえば、図中に「a」で示した正10角形は、中心軸の周りに回転させうるが、これにより、異なる配列パターンができる。同様の正10角形は、この図を外に向かって拡大していくと、その図形中に無数に存在していることから前記のことが理解される。
このペンローズパターンは、当初は単に興味深い平面充填パターンとして関心をもたれていただけであったが、後に発見された準結晶が、このペンローズパターンどおりの原子配置を持つことが判り、にわかに注目されるようになった。
準結晶は、液体状態から急冷したAlとMnの合金から発見された。初期のこの準結晶は不安定で、加熱するとより安定な結晶相が析出していたが、やがて安定な準結晶が続々と発見されている。
2011年には、最初にこの準結晶を発見したダニエル・シェヒトマンにノーベル化学賞が授与された。
ペンローズパターンは2次元の非周期性の平面充填構造であるが、実際の3次元準結晶ではどのような原子配列になっているのか興味あるところである。
シェヒトマンにより発見された準結晶の電子線回折図形は、結晶の回折図形のような回折スポットの集合であるにも関わらず、2回、3回の回転対称性に加え、結晶には存在しない5回対称性を示し、正20面体の持つ対称性を有していた。
その後に発見された準結晶Al-Ni-Co系などには、正10角柱と同じ対称性をもつ準結晶相も存在する。この準格子は2次元ペンローズパターンであり、この面が積層した構造をもつとされる。この場合、平面方向には準周期構造、これと垂直な軸方向には周期構造を有している。このほか、8角形相、12角形相の準結晶が見つかっている。
準結晶に特有の物性といったものはどうだろうか。金属元素から構成されたものとしては異常に高い電気抵抗があげられている。例えば、アルミニウム、銅、鉄は単体ではいずれも良導体であるが、これらからなる準結晶Al-Cu-Feでは電気抵抗が10万倍にも達し、周期構造の欠如が原因と考えられている。また、準結晶は、その非周期性のためへき開を形成し難く、このため比較的硬くて強靭である。それに、テフロン並みに低い表面エネルギーのものが見つかっていて、Al-Fe-Cu準結晶はフライパンのコーティング材として使用されているという。
これまで得られている準結晶は人工的に作られたものであるが、熱力学的に安定な平衡状態にあるとすれば、自然には存在しないものだろうかという疑問が沸く。
この点については、2016年に、宇宙からやってきた隕石中から準結晶が見つかったとの報告がされている。イタリア、フローレンス大学の地質学者Luca Bindi博士らのチームが極東ロシアのハトゥイルカ地方に5年前に落ちた隕石の破片の中に、数ミクロンの準結晶構造を見つけている。
この隕石の内部に準結晶構造が見つかったのは3度目のことであった。この準結晶もアルミニウム、銅、鉄の原子から構成されており、5回対称の構造を持っているとされる。
今年に入って、名古屋大学は2018年1月20日、豊田工業大学、東北大学、豊田理化学研究所との共同研究により、超伝導になる準結晶を世界に先駆けて発見したと発表した。この研究は、磁石や超伝導をもたらす「電子の長距離秩序」が準結晶では本質的に不在なのかを解明することを目的として行われ、Al、Zn、Mg の3元素を組み合わせ、高速急冷法により準結晶を合成し行われたものであった。
ペンローズは数学者であり、理論・宇宙物理学者でもある。米国の同じ理論・宇宙物理学者のリサ・ランドール(Lisa Randall、1962.6.18- )はペンローズタイプの準結晶の構造をとりあげて、その著書「ワープする宇宙・5次元時空の謎を解く」(原題 Warped Passages, 向山信治監訳 塩原通緒訳、2007年 NHK出版発行)の中で次のように述べている。
「余剰次元-(筆者注:われわれが存在している三次元空間とは別の次元のこと)-の痕跡が、あなたの台所にも隠れているかもしれない--と言ったら驚くだろうか。それは『準結晶』でコーティングした焦げつかないフライパンである。準結晶というのは不思議な構造で、その根本的な秩序は余剰次元でしか解明されない。ふつうの結晶は、原子や分子がきわめて対称的な格子状になって一定の基本配列で繰り返し並んでいる。三次元で結晶がどんな構造を形成するかはわかっているし、どんな並びがありうるかもわかっている。しかし準結晶における原子と分子の配列は、その並びのいずれとも合致しないのだ。
準結晶の並びの一例が、図2(筆者注:ペンローズタイルの図が示されている)である。ここには結晶に見られる厳密な規則性が欠けている。普通の結晶ならば、もっと方眼紙のマス目のようなものに見えるはずだ。この奇妙な物質の分子の並びを説明する最もエレガントな方法は、これを高次元の結晶構造の射影-三次元の影のようなもの-と見ることである。つまり、その並びは高次元空間での対称性をうちに秘めているのである。三次元においてはまったく不可解に見えた配列も、高次元世界においては秩序のとれた構造になる。準結晶でコーティングされたフライパンは、そのコーティングのなかの高次元結晶の射影と、もっとありふれた通常の三次元の食材との構造的な違いを利用しているわけだ。原子の配列が違うから、それぞれの原子が互いに結合することがない。これは余剰次元が実際に存在していて、いくつかの観測可能な物理現象を説明できることを強く示唆するものである。」
にわかに理解しがたい話であるが、どのように考えればいいのだろうか。数学者ペンローズが2次元平面における5回対称性を実現させるために考案したペンローズタイルは、準結晶の発見を通して、5次元空間との関連性を示し、宇宙物理学者ペンローズの元へと戻ってきた。あたかも、エッシャーのメタモルフォーゼの循環を見ている思いがする。















