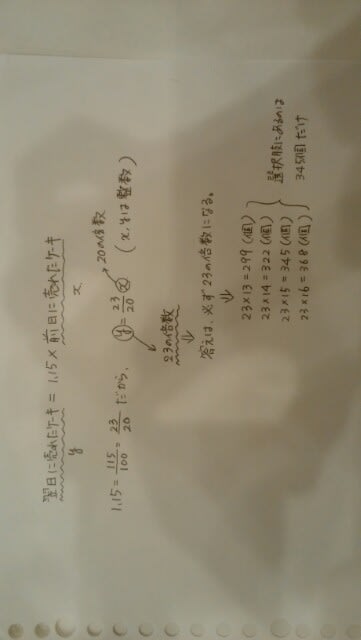下のグラフは、平成5年から平成20年までの漁業就業者数を年齢層別にまとめたものである。このグラフから判断できることとして、最も妥当なのはどれか。
①漁業就業者数は平成5年から5年毎に1割以上減少している。 ②55歳以上の就業者の構成比はすべての年で全体の50％以上である。 ③15～34歳の就業者は、平成20年では2万人に満たない。 ④平成5年の55～64歳の就業者数より、平成15年の65歳以上の就業者数の方が多い。 ⑤平成5年と平成20年で年齢階層別の漁業就業者数の変化をみると、55～64歳の変化が最も大きい。①漁業就業者は、平成15年は23.8、平成20年は22.2となっています。23.8×0.9＝21.42なので、1割も減少していません。ただ、それ以外は、確かに1割以上減少しています。②平成5年は、30.4＋18.0＝48.4％で、50％未満です。その他は50％以上。③15～34歳は、平成20年は、3.0＋7.6＝10.6％。全体が22.2万人だから、明らかに2万人以上です。④前者＝32.5×0.304＝9.88万人。後者＝23.8×0.333＝7.9254万人。前者の方が多い。よって、消去法により、正解は⑤です。⑤だけは、計算回数がかなり多くなるので、確かめない方が、実践的です。しかしながら、少し不満があります。普通、変化が大きいか小さいかは、変化率を調べます。それでいくと、一番変化が大きいのは、35～44歳で、約53.6％減少です。（55～64歳は、42％程度の減少）。また、率ではなくて、数の変化だとすると、確かに55～64歳の変化が最大です。この選択肢は、最後の部分を、「55～64歳の増減数が最も大きい。」とか、「55～64歳の変化数が最も大きい。」とかにすべきだと思うのですがねえ。
①漁業就業者数は平成5年から5年毎に1割以上減少している。 ②55歳以上の就業者の構成比はすべての年で全体の50％以上である。 ③15～34歳の就業者は、平成20年では2万人に満たない。 ④平成5年の55～64歳の就業者数より、平成15年の65歳以上の就業者数の方が多い。 ⑤平成5年と平成20年で年齢階層別の漁業就業者数の変化をみると、55～64歳の変化が最も大きい。①漁業就業者は、平成15年は23.8、平成20年は22.2となっています。23.8×0.9＝21.42なので、1割も減少していません。ただ、それ以外は、確かに1割以上減少しています。②平成5年は、30.4＋18.0＝48.4％で、50％未満です。その他は50％以上。③15～34歳は、平成20年は、3.0＋7.6＝10.6％。全体が22.2万人だから、明らかに2万人以上です。④前者＝32.5×0.304＝9.88万人。後者＝23.8×0.333＝7.9254万人。前者の方が多い。よって、消去法により、正解は⑤です。⑤だけは、計算回数がかなり多くなるので、確かめない方が、実践的です。しかしながら、少し不満があります。普通、変化が大きいか小さいかは、変化率を調べます。それでいくと、一番変化が大きいのは、35～44歳で、約53.6％減少です。（55～64歳は、42％程度の減少）。また、率ではなくて、数の変化だとすると、確かに55～64歳の変化が最大です。この選択肢は、最後の部分を、「55～64歳の増減数が最も大きい。」とか、「55～64歳の変化数が最も大きい。」とかにすべきだと思うのですがねえ。
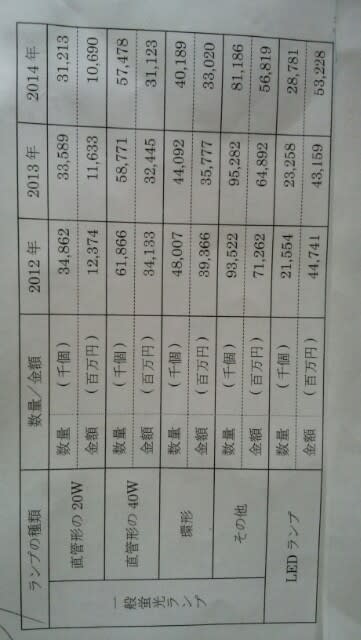①直管形の40Wの3ヵ年販売合計数量は、直管形の20Wのそれに対し2倍を超えている。 ②環形一般蛍光ランプにおいて2012年の数量と金額に対する2014年の数量と金額の増減率をみたとき、変化率がより大きいのは金額の方である。 ③一般蛍光ランプのうち、2012年の販売数量に対する2014年の販売数量の減少率が最も大きいのは直管形の20Wである。 ④2014年のLEDランプの1個当たりの平均単価は、環形一般蛍光ランプの2倍を超えている。⑤LEDランプの販売金額は、すべての年で一般蛍光ランプの販売合計金額の3分の1を超えている。
正解は④です。
正解は①です。
次に、選択肢を使ってやってみると、
正解は⑤です。
