以前、東大の教授が「子供の被ばくは年間1mSv/年以下でないとだめなんです」と泣いていました(泣き虫です)が、既に自然界からの被ばくが約1mSv/年あるのに、なぜ子供には被ばくが年間20mSv以下ではだめで、原発からの被ばくが年間1mSv以下でなければならないか、なぜ泣く必要があるのか、という疑問がどうしても払拭されず、私は原発事故に関する書籍を10冊以上読んでみました。
その中で一番科学的でわかりやすかったのが、「2時間でいまがわかる 放射能の真実!」 です。
です。
一方、「原発・放射能 子どもが危ない」 はかなり感情論に近い感じでした。子供には1mSv/年以下でなければならない根拠は「国」が法律でそう定めているからという理由らしく、その一方で、国の発表することは信用できないと、全くの論理矛盾でした。「国」が法律で決めた事というなら、妊娠可能な女子の腹部には3カ月で13ミリ・シーベルト以下にしなさい、妊娠中の女子の腹部に対して妊娠と診断された日から出産までの間に対しては10ミリ・シーベルト以下にしなさいと定めた医療法施行規則第30条の27(許容線量)では、年間1mSv以下にしなさいとは定められていません。
はかなり感情論に近い感じでした。子供には1mSv/年以下でなければならない根拠は「国」が法律でそう定めているからという理由らしく、その一方で、国の発表することは信用できないと、全くの論理矛盾でした。「国」が法律で決めた事というなら、妊娠可能な女子の腹部には3カ月で13ミリ・シーベルト以下にしなさい、妊娠中の女子の腹部に対して妊娠と診断された日から出産までの間に対しては10ミリ・シーベルト以下にしなさいと定めた医療法施行規則第30条の27(許容線量)では、年間1mSv以下にしなさいとは定められていません。
「2時間でいまがわかる 放射能の真実!」 を読んでわかった「原発からの被ばくが1mSv/年以下でなければならない」という主張の「根拠」をご紹介したいと思います。少し頭を使いますので、落ち着いてお願いします。
を読んでわかった「原発からの被ばくが1mSv/年以下でなければならない」という主張の「根拠」をご紹介したいと思います。少し頭を使いますので、落ち着いてお願いします。
(1) 1945年に広島・長崎で1Sv=1000mSv被爆した人の「ガン発症率」は、被爆しなかった人に比較して50%増えた。ただし、このデータでは125mSv以下の被爆量では「ガン発症率」は増えていなかった。
(Preston et al. Rad Res 2003;160:381)
↓
(2) 1000mSvの被爆で50%の増加ということは、100mSvでは5%の増加と推測する。
↓
(3) 日本人の30歳の生涯「ガン死亡率」は20%なので、20%の5%は1%。つまり、100mSvの被ばくで生涯「ガン死亡率」は1%増えると推測する。
↓
(4) 動物実験の結果では、慢性被ばくの場合の発ガン率は急性被ばくの発ガン率の2分の1~10分の1である。安全を考えて高い方の2分の1と仮定する。
↓
(5) 原発事故による住民の被ばくは慢性被ばくであり、(4)により100mSvで1%増加の2分の1、つまり100mSvで0.5%増と推測する。
↓
(6) 100mSvで0.5%%増加なら、1mSvでは0.005%増加、つまり10万人で5人増えると推測する。(この辺りが交通事故で死亡する確率と同等)
↓
(7) 以上により、子供の場合は感受性が高いと推測されるから、被ばくが1mSv/年以下でなければならない。
こんな感じの論理のようですが、以下の疑問が生じるのではないでしょうか。
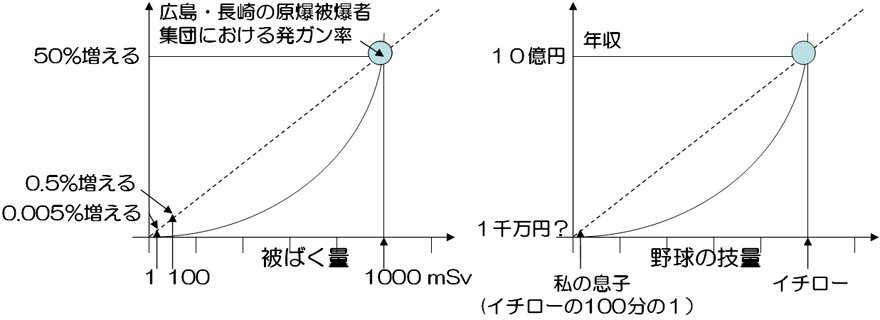
まずは、わかっている事は(1)だけということ、ここからのみ推測している事実を知って私自身驚きました。図左の丸で囲んだ事のみがわかっているだけなのです。
それに、(1)では「ガン発症率」なのに、いつの間にか(3)で「ガン死亡率」にすり替わっています。
さらに、(1)のデータでは125mSv以下の被爆量では「ガン発症率」は増えていないのです。
この論理の最大の欠点は、前回お伝えしたように、生命科学では2つのパラメーターは必ずしも一次関数の関係があると限りらないということです。(2)で10分の1のことをそのまま直線的に推測し、(6)で100分の1のことを直線的に推測しています。合計1000分の1のことを一次関数的に推測しています。(図左)
「1000倍の点と0点を直線で結び、1倍の時の結論を導き出す」、これはとても乱暴な科学だと思います。
図右をご覧下さい。イチローの年収がいくらなのか詳しくは知りませんが、10億円とします。野球に熱中している私の息子は、イチローの100分の1ぐらいの技量は持っていると思うのですが、それなら1000万円もらえるかということです。
あたりまえのことですが、野球の技量と報酬は一次関数的に比例するはずもなく、ある技量に達してやっと報酬が生まれる。つまり、点線で示された直線ではなく、実線で示された曲線の関係です。
以前、どれだけ運動すれば動脈硬化性疾患を予防できるかという記事の中で、毎日1時間歩くと、心筋梗塞の発症率0.074%を0.047%に、36%減少させるデータを載せました。生命科学を直線的に考えると、毎日2時間歩くと72%、毎日3時間歩くと心筋梗塞は発症しないことになってしまいます。こんな推測が間違いであることは誰にでもわかるはずです。
このような例を挙げればきりがありません。生命科学では2つのパラメーターは必ずしも一次関数の関係があると限りらない。むしろそうでないことの方が多いのです。
なるほど~と思われた方、こちらもぽちっと「ブログランキング」応援よろしくお願いいたします!
その中で一番科学的でわかりやすかったのが、「2時間でいまがわかる 放射能の真実!」
一方、「原発・放射能 子どもが危ない」
「2時間でいまがわかる 放射能の真実!」
(1) 1945年に広島・長崎で1Sv=1000mSv被爆した人の「ガン発症率」は、被爆しなかった人に比較して50%増えた。ただし、このデータでは125mSv以下の被爆量では「ガン発症率」は増えていなかった。
(Preston et al. Rad Res 2003;160:381)
↓
(2) 1000mSvの被爆で50%の増加ということは、100mSvでは5%の増加と推測する。
↓
(3) 日本人の30歳の生涯「ガン死亡率」は20%なので、20%の5%は1%。つまり、100mSvの被ばくで生涯「ガン死亡率」は1%増えると推測する。
↓
(4) 動物実験の結果では、慢性被ばくの場合の発ガン率は急性被ばくの発ガン率の2分の1~10分の1である。安全を考えて高い方の2分の1と仮定する。
↓
(5) 原発事故による住民の被ばくは慢性被ばくであり、(4)により100mSvで1%増加の2分の1、つまり100mSvで0.5%増と推測する。
↓
(6) 100mSvで0.5%%増加なら、1mSvでは0.005%増加、つまり10万人で5人増えると推測する。(この辺りが交通事故で死亡する確率と同等)
↓
(7) 以上により、子供の場合は感受性が高いと推測されるから、被ばくが1mSv/年以下でなければならない。
こんな感じの論理のようですが、以下の疑問が生じるのではないでしょうか。
まずは、わかっている事は(1)だけということ、ここからのみ推測している事実を知って私自身驚きました。図左の丸で囲んだ事のみがわかっているだけなのです。
それに、(1)では「ガン発症率」なのに、いつの間にか(3)で「ガン死亡率」にすり替わっています。
さらに、(1)のデータでは125mSv以下の被爆量では「ガン発症率」は増えていないのです。
この論理の最大の欠点は、前回お伝えしたように、生命科学では2つのパラメーターは必ずしも一次関数の関係があると限りらないということです。(2)で10分の1のことをそのまま直線的に推測し、(6)で100分の1のことを直線的に推測しています。合計1000分の1のことを一次関数的に推測しています。(図左)
「1000倍の点と0点を直線で結び、1倍の時の結論を導き出す」、これはとても乱暴な科学だと思います。
図右をご覧下さい。イチローの年収がいくらなのか詳しくは知りませんが、10億円とします。野球に熱中している私の息子は、イチローの100分の1ぐらいの技量は持っていると思うのですが、それなら1000万円もらえるかということです。
あたりまえのことですが、野球の技量と報酬は一次関数的に比例するはずもなく、ある技量に達してやっと報酬が生まれる。つまり、点線で示された直線ではなく、実線で示された曲線の関係です。
以前、どれだけ運動すれば動脈硬化性疾患を予防できるかという記事の中で、毎日1時間歩くと、心筋梗塞の発症率0.074%を0.047%に、36%減少させるデータを載せました。生命科学を直線的に考えると、毎日2時間歩くと72%、毎日3時間歩くと心筋梗塞は発症しないことになってしまいます。こんな推測が間違いであることは誰にでもわかるはずです。
このような例を挙げればきりがありません。生命科学では2つのパラメーターは必ずしも一次関数の関係があると限りらない。むしろそうでないことの方が多いのです。
なるほど~と思われた方、こちらもぽちっと「ブログランキング」応援よろしくお願いいたします!