毎日いろんなことで頭を悩ましながらも、明日のために頑張ろうと自分を励ましています。
疲れるけど、頑張ろう!
数学の美しさ
2011年09月25日 / 塾
私立中模試からの出題。場合の数の問題で、見かけは簡単そうだが、論理的に考えていかないとこんがらがってしまって正解にたどり着けない。なかなか厄介な問題だ・・。
【問い】

上の図は、1辺の長さが1cmの正三角形を24個使って正六角形をつくったものです。点Pは、図形の真ん中の点Oを出発して、正三角形のそれぞれの辺上を毎秒1cmの速さで動きます。
このとき、点Pが点Oを出発し、4秒後に点Oにある進み方は全部で何通りありますか。ただし、同じ辺や点を何回通ってもよいものとします。
この問題の対象である小6年生は言うまでもなく、国立大学合格を目指す浪人生にも解かせてみたができなかった。偉そうに言う私でさえも、正解を導き出すのにかなり苦労した・・。
だが、世の中には頭のいい人はいくらでもいるもので、「この問題はこうやって解くんだぞ」と理路整然として、美しくさえある模範解答が教師用の解説に載っていた。それを見て、「私にはとても思いつけない」とすぐに脱帽してしまったほどなので、以下にその解法を載せておくことにする。
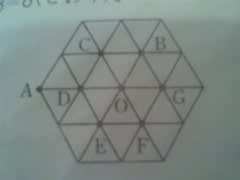
最初の1秒をOBと進む場合を考える。
①最後の1秒(3~4秒後)がBOのとき、2秒かけてBからBにもどればよいから、6とおり。
②最後の1秒がCOのとき、BからCへ2秒で行けばよいから、2とおり。
③最後の1秒がDOのとき、BからDへ2秒で行けばよいから、2とおり。
④最後の1秒がEOのとき、BからEへ2秒で行けばよいから、1とおり。
⑤最後の1秒がFOのとき、③と同様に2とおり。
⑥最後の1秒がGOのとき、②と同様に2とおり。
よって、あわせて、6+2+2+1+2+2=15(とおり)。
最初の1秒がOC、OD、OE、OF、OGのときもそれぞれ15とおりずつあるから、全部で、15×6=90とおり。
素晴らしい!!
数学の美しさには時々驚かされる。高校の時にもっと数学が好きだったら、もうちょっと違う人生を歩んでこれたかも・・。
【問い】

上の図は、1辺の長さが1cmの正三角形を24個使って正六角形をつくったものです。点Pは、図形の真ん中の点Oを出発して、正三角形のそれぞれの辺上を毎秒1cmの速さで動きます。
このとき、点Pが点Oを出発し、4秒後に点Oにある進み方は全部で何通りありますか。ただし、同じ辺や点を何回通ってもよいものとします。
この問題の対象である小6年生は言うまでもなく、国立大学合格を目指す浪人生にも解かせてみたができなかった。偉そうに言う私でさえも、正解を導き出すのにかなり苦労した・・。
だが、世の中には頭のいい人はいくらでもいるもので、「この問題はこうやって解くんだぞ」と理路整然として、美しくさえある模範解答が教師用の解説に載っていた。それを見て、「私にはとても思いつけない」とすぐに脱帽してしまったほどなので、以下にその解法を載せておくことにする。

最初の1秒をOBと進む場合を考える。
①最後の1秒(3~4秒後)がBOのとき、2秒かけてBからBにもどればよいから、6とおり。
②最後の1秒がCOのとき、BからCへ2秒で行けばよいから、2とおり。
③最後の1秒がDOのとき、BからDへ2秒で行けばよいから、2とおり。
④最後の1秒がEOのとき、BからEへ2秒で行けばよいから、1とおり。
⑤最後の1秒がFOのとき、③と同様に2とおり。
⑥最後の1秒がGOのとき、②と同様に2とおり。
よって、あわせて、6+2+2+1+2+2=15(とおり)。
最初の1秒がOC、OD、OE、OF、OGのときもそれぞれ15とおりずつあるから、全部で、15×6=90とおり。
素晴らしい!!
数学の美しさには時々驚かされる。高校の時にもっと数学が好きだったら、もうちょっと違う人生を歩んでこれたかも・・。
コメント ( 0 ) | Trackback ( 0 )




