Arandaモデル 4支族2階層
(2021年11月5日)すべて個人は支族、階層、サブセクションの座標を持ち、その仕組のなかで分類される、ここをWeilが注目した。
<les individus, hommes et femmes, sont répartis en classes, la classe de chacun étant déterminée, d’après certaines règles, par celles de ses parents ; et les règles du mariage indiquent, suivant les classes…> 男も女も個人は階層に分かれている。それぞれの階層は幾つかの規則によって定義され、特に両親の決まり方の規則が重要で、婚姻の規則にもこの階層が影響する(同)。
「両親の決まり方...」は奇妙な訳だがこれはMurngin族などオーストラリア先住民では生まれた子は実の両親に属さず、他の集団に預けられる「養子制度」を言い換えている。養子先の決め方には規則が設けられ、これが階層を形成する基準になる。規定に沿って、実親が所属する集団からは「養子先」が決定され、親は粛々と子を預ける。この過程が「両親の決まり方」となる。
その決まり方で子が生きる座標が決まる。子の座標は実親のそれを受け継がず、帰属する養子先の数値を持つことになる。
<la totalité des mariages possibles peut donc se répartir en un certain nombre de types distincts>婚姻可能の総体は、幾つかの分別可能な形式に集約される。親の婚姻の仕組み、その子が仕向けられる養子先の割当で子の婚姻が決まる。
婚姻を分別する条件(conditions)を2(A,B)に分ける。
A) Pour tout individu, homme ou femme, il y a un type de mariage et un seule qu’il (ou elle) a le droit de contracter.
B) Pour tout individu, le type de mariage qu’il (ou elle) est susceptible de contracter dépend uniquement de son sexe et du type de mariage dont il (ou elle) est issu. (267頁)
A : 男女を問わず婚姻は一つの決まり
B : 婚姻の決まりは個の性と彼(彼女)の父母がどのような婚姻形態を経たか、で決まる
婚姻をMとし、Mi(1,2,3…n)とする。
とある数学重鎮が断った「心が絡む」を一切排除して規則で婚姻を決める、すると最も合理的な制度の創造に向かう…ヴェイユの智の有様が理解できる訳です。Aranda族のモデルを用い一の部族に4階層を設定する。写真は258頁から。
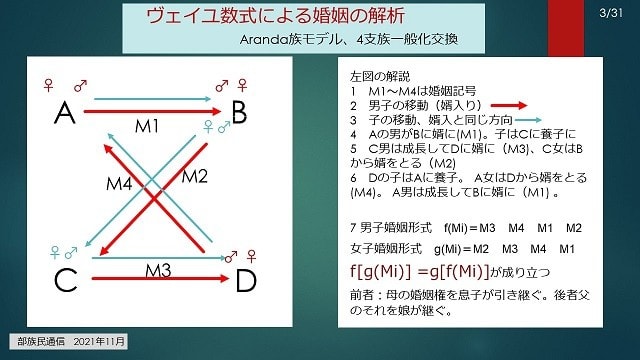
Aが男をBに贈る(婿にやる)、BはCに、以下矢印の進みです。
女Bが男Aを婿にして子を生む。その子はCに移る。Cに養子になった男は成人してDに婿に出る(M3)、女CはCに残り、成人ののちBから婿を貰う。Dにて生まれる子はAに養子(M4)。以下この規則で子を婿が矢印に沿って周回交換される。女子は養女にとどまり1周回遅れてBに養子に出された男子を婿にとる。この男子はA女が生んだ子で、女子には母の兄弟の息子。交差いとこである。男子は養子と婿で周回2の先で女を嫁とする(4階層で社会を形成するAranda族などアボリジニ多くのの規則)。
Weil数式でこの子と婿の周回交換を
婚姻の形式=M1 M2 M3 M4
男子の婚姻形式 f(Mi)=M3 M4 M1 M2
女子の婚姻形式 g(Mi)=M2 M3 M4 M1
となる。これをパワーポイントで図式化した。

(参考図、前回掲載、4階層を婿と子(男女)が順に隣接支族に移動する様(一般化交換)が理解出来るかと)
第3の条件を提示する
(C)Tout homme doit pouvoir épouser la fille de sa mère.(男は母の兄弟の娘と婚姻を結ぶ)
Miから派生するf(Mi)とg(Mi)は周回が同様なので以下の式が成立する。
f[g(Mi)]=g[f(Mi)]
これを男子の方式と女子のそれは「一回遅れながら同じ周回の様を見せる」と単純に(勝手に)解釈します。数学での意味合いを知る方は異なる理解かと想像します。
(上の図は参考、前回掲載、交換の様を展開した)

上の上の図ではf[g(Mi)]=g[f(Mi)]が理解しにくいかと。そこで計算式の仕組みを上図に解説した。図の説明通りで婚姻M(a,b)で生まれる子の帰属先を(a+1,b+1)と決める。その数値がABCDの各アドレスと整合する。
そこで生まれた子の婚姻権(fonction)は男はf(a+c+1,b+c,c+1)、女はg(a,b,c)となる。cはその子がどのようにして貰われたか(水平は1、たすきは0)。f[g(Mi)]の意味合いはg母親の権利を息子fがどのように引き継ぐかの数字。g[f(Mi)]はf父親の権利を娘に。それらが合致=すれば交差いとこ婚が成立する。
階層あるいはセクションのアドレスを振り、婚姻Mを数字(a,b,c)での特定し、子の配属を計算式で決める。その子の婚姻権を同じく数値で決めて、男女を替える。すると父親の娘、母親の息子の婚姻権が数値化される。それが同等ならそのアドレスで婚姻する(男の婿行の地と女の婿とり地がおなじになる)。これがヴェイユ式の思想です。
今回例として4支族を取り上げたが、ヴェイユは8サブセクションで展開する。お楽しみを。
親族の基本構造第一部の補遺2 ヴェイユの証明 1 (2021年11月5日)了
(2021年11月5日)すべて個人は支族、階層、サブセクションの座標を持ち、その仕組のなかで分類される、ここをWeilが注目した。
<les individus, hommes et femmes, sont répartis en classes, la classe de chacun étant déterminée, d’après certaines règles, par celles de ses parents ; et les règles du mariage indiquent, suivant les classes…> 男も女も個人は階層に分かれている。それぞれの階層は幾つかの規則によって定義され、特に両親の決まり方の規則が重要で、婚姻の規則にもこの階層が影響する(同)。
「両親の決まり方...」は奇妙な訳だがこれはMurngin族などオーストラリア先住民では生まれた子は実の両親に属さず、他の集団に預けられる「養子制度」を言い換えている。養子先の決め方には規則が設けられ、これが階層を形成する基準になる。規定に沿って、実親が所属する集団からは「養子先」が決定され、親は粛々と子を預ける。この過程が「両親の決まり方」となる。
その決まり方で子が生きる座標が決まる。子の座標は実親のそれを受け継がず、帰属する養子先の数値を持つことになる。
<la totalité des mariages possibles peut donc se répartir en un certain nombre de types distincts>婚姻可能の総体は、幾つかの分別可能な形式に集約される。親の婚姻の仕組み、その子が仕向けられる養子先の割当で子の婚姻が決まる。
婚姻を分別する条件(conditions)を2(A,B)に分ける。
A) Pour tout individu, homme ou femme, il y a un type de mariage et un seule qu’il (ou elle) a le droit de contracter.
B) Pour tout individu, le type de mariage qu’il (ou elle) est susceptible de contracter dépend uniquement de son sexe et du type de mariage dont il (ou elle) est issu. (267頁)
A : 男女を問わず婚姻は一つの決まり
B : 婚姻の決まりは個の性と彼(彼女)の父母がどのような婚姻形態を経たか、で決まる
婚姻をMとし、Mi(1,2,3…n)とする。
とある数学重鎮が断った「心が絡む」を一切排除して規則で婚姻を決める、すると最も合理的な制度の創造に向かう…ヴェイユの智の有様が理解できる訳です。Aranda族のモデルを用い一の部族に4階層を設定する。写真は258頁から。
Aが男をBに贈る(婿にやる)、BはCに、以下矢印の進みです。
女Bが男Aを婿にして子を生む。その子はCに移る。Cに養子になった男は成人してDに婿に出る(M3)、女CはCに残り、成人ののちBから婿を貰う。Dにて生まれる子はAに養子(M4)。以下この規則で子を婿が矢印に沿って周回交換される。女子は養女にとどまり1周回遅れてBに養子に出された男子を婿にとる。この男子はA女が生んだ子で、女子には母の兄弟の息子。交差いとこである。男子は養子と婿で周回2の先で女を嫁とする(4階層で社会を形成するAranda族などアボリジニ多くのの規則)。
Weil数式でこの子と婿の周回交換を
婚姻の形式=M1 M2 M3 M4
男子の婚姻形式 f(Mi)=M3 M4 M1 M2
女子の婚姻形式 g(Mi)=M2 M3 M4 M1
となる。これをパワーポイントで図式化した。

(参考図、前回掲載、4階層を婿と子(男女)が順に隣接支族に移動する様(一般化交換)が理解出来るかと)
第3の条件を提示する
(C)Tout homme doit pouvoir épouser la fille de sa mère.(男は母の兄弟の娘と婚姻を結ぶ)
Miから派生するf(Mi)とg(Mi)は周回が同様なので以下の式が成立する。
f[g(Mi)]=g[f(Mi)]
これを男子の方式と女子のそれは「一回遅れながら同じ周回の様を見せる」と単純に(勝手に)解釈します。数学での意味合いを知る方は異なる理解かと想像します。

(上の図は参考、前回掲載、交換の様を展開した)

上の上の図ではf[g(Mi)]=g[f(Mi)]が理解しにくいかと。そこで計算式の仕組みを上図に解説した。図の説明通りで婚姻M(a,b)で生まれる子の帰属先を(a+1,b+1)と決める。その数値がABCDの各アドレスと整合する。
そこで生まれた子の婚姻権(fonction)は男はf(a+c+1,b+c,c+1)、女はg(a,b,c)となる。cはその子がどのようにして貰われたか(水平は1、たすきは0)。f[g(Mi)]の意味合いはg母親の権利を息子fがどのように引き継ぐかの数字。g[f(Mi)]はf父親の権利を娘に。それらが合致=すれば交差いとこ婚が成立する。
階層あるいはセクションのアドレスを振り、婚姻Mを数字(a,b,c)での特定し、子の配属を計算式で決める。その子の婚姻権を同じく数値で決めて、男女を替える。すると父親の娘、母親の息子の婚姻権が数値化される。それが同等ならそのアドレスで婚姻する(男の婿行の地と女の婿とり地がおなじになる)。これがヴェイユ式の思想です。
今回例として4支族を取り上げたが、ヴェイユは8サブセクションで展開する。お楽しみを。
親族の基本構造第一部の補遺2 ヴェイユの証明 1 (2021年11月5日)了



























※コメント投稿者のブログIDはブログ作成者のみに通知されます