大人の数学教室085(場合の数④)

【第4章】

(2)順列

異なるn 個のものうちr 個取り出し、

順番を考え1列に並べたものを、

n 個からr 個取り出した「順列」という。

その並べ方の総数を P[n,r] と表す。

(※本来の記号は、Pの左に小さくn、右に小さくrを書く。)

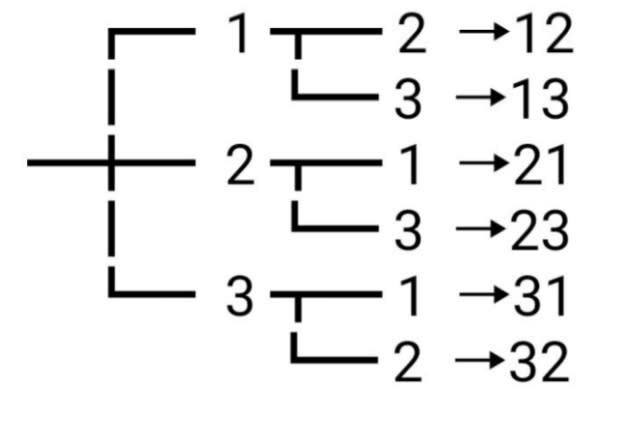
例9)1 から5 までの数字のうち、2 個を使って2桁の数を作る。何個できるか。ただし、同じ数字は使えない。

【解】

十の位は、5 個のうちのいずれかで、5 通り

一の位は、5 個のうち十の位に使ったもの以外で、4 通り

積の法則より、5×4=20 (個)

P[n,r] を求めてみよう。

1 番目は、n 個のうちのいずれで、n 通り

2 番目は、n 個のうち1 番目に使ったもの以外で、n-1 通り

…

k 番目は、n 個のうち1 からk-1 番目までに使ったもの以外で、n-(k-1)=n-k+1 通り

よって、

P[n,r] =n×(n-1)×……×(n-r+1)

n を先頭に、1 ずつ減らした数をr 個掛けたものである。

r=n のとき、n 個すべての順列

P[n,n] =n×(n-1)×…×2×1

1 からn までの積を n の「階乗」といい、n! で表す。

n!=P[n,n]=n×(n-1)×…×2×1

例10)9 人で野球をするときに、打順を何通りあるか。

【解】

P[9,9]=9!=9×8×7×6×5×4×3×2×1

=362880 (通り)

n≠rのとき、P[n,r]×(n-r)!=n!…★

n=rのとき、上の式に当てはめると、

P[n,n]×0!=n!

0!=1となれば成り立つ。

★式が成り立つように、

0!=1 と定義する。

P[n,r]=n!/(n-r)!

(例)P[7,3]=7!/4!

大人の数学教室084(場合の数③)

【第3章】

【積の法則】

A の起こり方が m 通り，そのおのおのに対して B の起こり方が n 通りあるとき， A と B が両方起こる場合の数は m×n 通りである。

例6)A,B 2個のサイコロを同時に振る。A の出た目をa、B の出た目をb とする。a が偶数で、bが6 の約数となるのは何通りあるか。

【解】

a が偶数となるのは、3 通り

b が6 の倍数となるのは、4 通り

よって、3×4=12 (通り)

例7)サイコロを振って出た目をaとする。1組52枚のトランプから1枚抜く。

a が偶数で、トランプがダイヤである場合は何通りか。

【解】

aが偶数となるのは、3 通り

トランプがダイヤとなるのは、13通り

よって、3×13=39 (通り)

3つ以上の積の法則

Ai の起こり方がm[i] 通りのとき、A1,…,An が同時に起こる場合の数は、

m[1]×…×m[n] 通りである。

【和の法則と積の法則の違い】

和の法則のX,Y は、同じレベルの事柄である。

積の法則のA,B は、無関係の事柄も可能である。

【約数の個数と和】

例8)12 の約数の個数および約数の和を求めよ。

【解】

12=2^2×3 だから、

約数は2^s×3^t (s=0,1,2 t=0,1)

sは3通り、tは2通り

よって、3×2=6 (個)

(1+2+22)(1+3) を展開すると、すべての約数の和になる。

(1+2+2^2)(1+3)=7×4=28

【確かめ】12の約数は、1,2,3,4,6,12

自然数n を素因数分解する。

n=(p1)^t[1]×…×(pm)^ t[m]のとき、

p1,…,pm は素数

n の約数は、

(t[1]+1)×…×(t[m]+1) 個である。

n の約数の和は、

｛1+p1+…+(p1)^t[1]｝×…×｛1+pm+…+(pm)^t[m]｝

大人の数学教室083(場合の数②)

【第2章】

【和の法則】

XとYという２つの事柄があり、XとYは同時には起こらないとする。Xの起こるのがｍ通り、Yが起こるのがｎ通りあるとき、

XまたはYが起こる場合の数は、

ｍ＋ｎ通りとなる。

すべての事柄Uを、次のn 個の集合Pk (k=1,…,n)に分ける。

P[i]∩P[j]=Φ (i≠j), P[1]∪…∪P[n]=U

A が何通りあるか考えるのに、

A=P[1]∪…∪P[m]とし、P[k]の中でAであるのがp[k] 通りあるとする。

A は、p[1]+…+p[n] 通りある。

例3)1組52枚のトランプから1枚を抜くとき、絵札となるのは何通りか。

【解】

各マーク3通りずつだから、3×4=12 (通り)

【イメージ】

P[1]=ダイヤ♦️、P[2]=クローバー☘️

P[3]=ハート♥️、P[4]=スペード♠️

絵札は、p[1]=p[2]=p[3]=p[4]=3

例4)A,B 2個のサイコロを同時に振る。A の出た目をa、B の出た目をb とする。和a+b が5 または6 となるのは何通りあるか。

【解】

目の和が5 となるのは、

(a,b)=(1,4)(2,3)(3,2)(4,1) の4 通り

目の和が6 となるのは、

(a,b)=(1,5)(2,4)(3,3)(4,2)(5,1) の5 通り

同時に起きないので、4+5=9 (通り)

例5)A,B 2個のサイコロを同時に振る。A の出た目をa、B の出た目をb とする。2a-b>0 となるのは何通りあるか。

【解】

a=1 のとき、b=1 の1 通り

a=2 のとき、b=1,2,3 の3 通り

a=3 のとき、b=1,2,3,4,5 の5 通り

a≧4 のとき、b=1,2,3,4,5,6 の6 通り

よって、1+3+5+6+6+6=27 (通り)

<イメージ>

全体集合U の部分集合X,Y、

X∩Y=Φ のとき、n(X∪Y)=n(X)+n(Y)

大人の数学教室082(場合の数①)

ことがらが何通りあるかを考えてみよう。

【第1章】

(1)場合の数

例1)1,2,3 の3つの数字を使って2 桁の数を作る。何個の数が作れるか。

【解】12,13,21,23,31,32 の6個

例2)5円玉3枚、10円玉3枚を使って支払える金額は何通りあるか。

【解】5円玉の数と10円玉の数、合計金額を表にすると、

a=5円玉の枚数、b=10円玉の枚数とする。

(a,b)=(0,1)(0,2)(0,3)→10,20,30

(a,b)=(1,0)(1,1)(1,2)(1,3)→5,15,25,35

(a,b)=(2,0)(2,1)(2,2)(2,3)→10,20,30,40

(a,b)=(3,0)(3,1)(3,2)(3,3)→15,25,35,45

よって、

5,10,15,20,25,30,35,40,45の9通り

場合の数を求めるとき、

もれなく重複なく数える必要がある。

例1) を次のように解くことができる。

考えられる場合を、木の枝分かれのように図示することで、もれなく重複なく考えることができる。木の枝分かれのような図を「樹形図」という。場合の数を考えるのに有益である。

x^2+x+1で割った余り

2020x^2020+2021x^2021+2022x^2022

をx^2+x+1で割った余りを求めよ。