相対性理論の含意する世界観
四次元世界の遠近法
相対性理論が自然に適用される世界は極大宇宙である。ここで極大という意味は、天文学的な意味での大宇宙をあつかうということだけではなく、非常に高いエネルギーや極端に大きな重力場が存在するような場合をも含んでいる。古典物理学の実験観察が基礎としていた人間的尺度で考えるならば、この理論には、我々の常識を逆なでする所が多々あることはよく知られている。例えば、相対性理論の基本原理である一慣性系における一光の相対速度の不変性という原理は、我々が、たとえ光速度の99.9%の速度で光を追いかけたとしても、もとの光を依然として前と同じ速さで見いだすであろうという逆説的事態を主張している。実際、絶対基準系(絶対静止のエーテル)に対する地球の運動の影響を測定しようとしたマイケルソン・モレーの実験が否定的な結果を与えるまでは、アインシュタインを除く殆どの古典物理学者は、このような逆説を物理学の基本原理として受け入れることを拒否していたといってよい。例えば、ローレンツは、光速度の不変性という事実を、エーテルが運動物体に与える収縮効果と、エーテルが運動する時計に与える遅延効果が、互いに相殺した結果生じた「見かけ上の現象」であると考えていた。彼は、「エーテル」という隠れた実在が及ぼす未知の因果的効果によって、絶対的な意味で運動物体が収縮し、運動する時計が遅れる、と考えたのである。絶対静止系を前提したローレンツにとって、光速度の不変性は、説明されるべき変則的事実であって、決して物理学の普遍的な原理などではなかったのである。「運動物体の収縮」および一運動する時計の遅れ」という二つのアイデアは、ローレンツ変換とともに、アインシュタインの特殊相対性理論にも登場するが、その物理的解釈は本質的に変化したといってよい。相対性理論では、この二つの効果は、どの慣性系を基準にしても平等に現れるから、絶対静止のエーテルに起因するものと考えることができないからである。それは、時空の計量の定義にかかわる本質的問題となり、複数の原理的に対等な時間系列の存在と、絶対的同時性の否定という相対性理論の核心ともいうべき基本思想から説明されるのである。そして、この相対性理論の核心部分は、絶対時間と絶対空間という概念に基づいて構成されたニュートン物理学の根幹を否定するものなのである。
我々は、相対性理論がニュートン物理学の連続線上に構想されたものではないことを明瞭に理解しなければならない。ニュートン物理学との不連続性を見失わないことは、相対性理論を理解するうえで必要不可欠であるにもかかわらず、しばしば見落とされる。その理由は、相対性理論の立場からニュートン物理学を光速度を無限大とする極限操作によって数学的に導くことができるために、数学的な一般化という事実が、意味論的な本質的相違点を覆い隠しているからである。ニュートン物理学は、厳密には真ではないが、物体の速度が光速度に比べて小さいときは、近似的に真となるという意味で、相対性理論のなかに包摂されているということは確かに誤りではない。ひとたび、相対性理論のパラダイムを受け入れるならば、その立場にたってニュートン物理学を受容することは可能である。しかしながら、相対性理論というひろい枠組みのなかに包摂されたニュートン物理学は、元来のニュートン物理学がそれ自身のパラダイムの枠組みのなかでもっていた意味を失っていることに注意しなければならない。
そのことは、次のような考察によって明らかとなる。相対性理論では四次元の時空は、過去と未来を向いた二つの光円錐によって、三つの領域、すなわち絶対未来、絶対過去、共時的(空間的)領域の三つに別れる。基準事象O(今此処)から見て、絶対未来とは、如何なる慣性基準系においても未来となる領域であり、絶対過去とは、如何なる慣性基準系においても過去となる領域である。相対性理論に固有の時空的領域は共時的(空間的)領域であり、そこにある事象は、基準系の取り方によってOの未来にも過去にも現在にもなりうるという意味で、生起の時間的順序が完全に相対化されている。我々は、このような共時的領域はニュートン物理学では存在しえない領域であることに注意しなければならない。
さて、相対論で光円錐を図解するときにには、時間軸と空間軸を二等分するかたちで光円錐を表示するのが慣例であるが、これは光速度c=1という尺度を採用したことを意味している。人間の日常的な尺度では、光速度cは極端に大きな値であるから、実際の光円錐は空間軸に限りなく接近するために、相対論に固有の領域である共時的領域も限りなくニュートン物理学の絶対的に同時的な領域に縮退していくように見える。しかしながら、このような数学的極限操作によって相対性理論の時空概念がニュートン物理学の時空概念に移行するという考え方は、厳密にいって誤りなのである。1/cがゼロでなくて有限の値であることは、両者の概念の間の連続的移行を不可能にするということを以下に示そう。
共時的領域とは何であるかということを明確に示すために、「基準系fでは出来事xが出来事yよりも前に起きた」という関係をA(x,y,f)で、「基準系fでは、出来事xが出来事yと同時に起きた」という関係をS(x,y,f)で表記しよう。
出来事xに関して、xの絶対的未来領域、xの絶対的過去領域、xの絶対的な同時的領域、および共時的領域という三つの概念を次のように、時空の計量に言及しない形で区別することができる。今、出来事xの(因果的)未来領域に属する出来事を、
F(x)={y|(∀f)A(x,y,f)}
出来事xの(因果的)過去領域に属する出来事を、
P(x)={y|(∀f)A(y,x,f)}
出来事xと絶対的な同時的領域に属する出来事を
S(x)={y|(∀f)|S(x,y,f)}
出来事xと共時的な領域に属する出来事を
C(x)={y|(∃f)S(x,y,f)}
と書けば、相対性理論とニュートン物理学の時空概念の本質的な相違点は次のように表現できよう。
ニュートン物理学では、xと共時的な領域C(x)はそもそも存在せず、任意のx,yに対してy∈P(x) または y∈S(x) または y∈F(x)
のどれかが、そしてどれか一つのみが、かならず成り立つのに対して、
相対性理論では、xと絶対的に同時的な領域S(x)はそもそも存在せず、任意のx,yに対して y∈P(x)または y∈C(x) または y∈F(x)のどれかが、そしてどれか一つのみが、かならず成り立つ。
そして、共時的領域にとって本質的なことは、「.....と共時的である」という関係が推移律を満たすとは限らないということにある。即ち、事象aとbが共時的であり、事象bと事象cが共時的であっても、事象aと事象cとは共時的とは限らないのである。それは、aとbとを同時的とするような基準系と、bとcとを同時的とする基準系がそれぞれに存在したとしても、この二つの基準系が一致するとはかぎらないということに由来するのである。
そして、空間的に隔てられた二つの事象が、あらゆる基準系で同時的となることは、相対性理論においては起こりえないのである。
したがって、「共時性」とは、弱められた意味での「同時性」なのではない。その理由は、上で示されたように、共時的な領域に属する出来事については、絶対的な同時性の概念が否定されることによって、時間的な継起の概念もまた相対化されるからである。すなわち、互いに共時的な二つの事象は、基準系の取り方によって、どちらが先に起きたかが変わりうるからである。すなわち
C(x)={y|(∃f)S(x,y,f)}={y|(∃f)A(x,y,f)&(∃g)A(y,x,g)}
相対性理論は、光速度を無限大とする極限においては(正確には、物体の速度vと光速度の比がゼロとなる極限においては)ニュートン物理学と一致するということがよくいわれる。しかし、その意味は、光速度が物体の運動速度に比べて非常に大きい場合には、相対性理論はニュートン物理学と同じ観測結果を予言するということであって、相対性理論の時空概念とニュートン物理学の時空概念の区別がなくなるという意味ではない。
なるほど、1/c がきわめて小さい場合には、共時的領域C(x)は、(光円錐が無限に空間軸に接近するために)ニュートン物理学でいう絶対的同時領域に限りなく接近するであろう。しかしながら、両者の意味するものは上で示した通り全く異なっており、決して同一視できないことに注意しなければならない。1/cがゼロではなくて有限の値をとるということ、しかもそれがあらゆる慣性系でつねに同一の値をとるということが、ニュートン物理学と相対性理論との間の不連続性を形成するのである。
相対性理論では、絶対的基準系の存在を否定したのではなく、観測できない実体を切り捨てる「オッカムの剃刀」の原理にもとづいて、単にその存在を前提しないですませたという言い方が科学史の文献にはかなり見られる。
しかし、もし絶対的同時性という概念を、「あらゆる慣性基準系で同時的」という意味にとるならば、このような解釈はミスリーディングであることが分かるだろう。「絶対時間はありえない」という主張は相対性理論のメッセージの核心にあるのである。
我々は、計量を捨象して四次元の時空の構造を根拠に語ったが、計量を明示した場合には、さらにニュートン物理学と相対性理論の時空の遠近法はさらに明瞭になることを次に示そう。ニュートン物理学では、時間的な近さと空間的な近さは、それぞれ独立であって、ある出来事の時空的なε近傍は、時間をdt、空間距離をdlとして|dt|<ε かつ |dl|<εによって表示される。要するに、ニュートン物理学の遠近法は、近傍が有界な閉じた領域を形成するという意味で、基本的には常識と一致するといってよかろう。
これに対して、相対性理論の遠近法は、時間と空間とが不可分離的であるために、時間的にも空間的にも無限に延長する、開かれた概念であるという特徴を持っている。
それは四次元ミンコフスキー時空におけるε近傍が、時間的にも、空間的にも双曲的な構造を持つことに表されている。ミンコフスキー時空では、(光速度c=1として)座標時間の経過をdtで、空間座標で表示された距離をdl(dl=(dx
2+dy
2+dz
2)
1/2)として、時間的な四次元距離はds
2=dt
2-dl
2によって、空間的な四次元距離はds
2=dl
2-dt
2で表示されるから、四次元時空のε近傍は、ニュートン物理学のように、|dt|<ε かつ |dt|<εのような閉じた領域によって与えられるのではなく、|ds|<εによって与えられる双曲的な超曲面で囲まれた領域で表示される。それゆえに、この時空における「今此処」の近傍は光円錐に沿って過去と未来へ向かって限りなく延長しているのである。
時間的 ε 近傍 空間的 ε 近傍

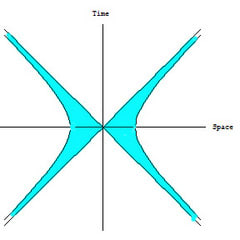
相対性理論におけるε近傍が時間軸と空間軸に沿って無限のかなたに伸びているということは、あまりよく認識されていないのではないだろうか。それは、ニュートン物理学のなかで、あるいはニュートン物理学がその洗練にすぎない我々の日常言語の「近傍」概念とはあまりにもかけ離れているように見えるからである。ここでも、我々はc→∞の極限操作によって、事態を単純化しようとするかもしれない。つまり、cを限りなく大きくすれば、時間的近傍は限りなく絶対現在の領域に近づき、共間傍時近時的領域にあらわれる空間的近傍は無視しうるのではないかと考えるのである。しかしながら、相対論でいう時空の四次元距離の概念にとって、基準系の変換に対して不変であるのは、四次元距離体であって、そのなかに現れるdtやdlではないということが、ここで重要な意味を持ってくる。それは、言い換えるならば、空間を捨象した「今」や、時間を捨象した「此処」という概念に、不変の意味がないということを意味している。そのために、ニュートン物理学では、時間的近傍と空間的近傍とは独立の概念であって、二つの出来事が時間的に接近しており、なおかつ空間的にも接近していると述べることに何の矛盾もないが、相対性理論では、二つの出来事が接近しているという場合、それは「空間的に接近しているか(space-likeな四次元距離の意味で)それとも「時間的に接近しているか(time-likeな四次元距離の意味で)」どちらか一つだけを意味するのであって、「時間的な四次元距離の意味で近傍にあり、かつ空間的な四次元距離の意味でも近傍にある」ということはできないのである。
我々が日常的な地上の出来事について語る場合、ニュートン物理学で事が足りるから、一々相対性理論を持ち出す必要がないというのは、もしそれが、相対論的宇宙論は我々の日常生活とは無関係であるという意味でならば、正しくない。有名なオルバースのパラドックスは、夜空が暗いのはなぜであるかという日常的には自明の理にすぎぬことを問題にしたものであるが、現代の物理学者は、これをビッグバン宇宙論と関連させて説明しているからである。また、このような例を持ち出すまでもなくとも、我々は、一度、天空を見上げ、人間的尺度をはるかに越える宇宙について観想するならば、むしろ相対性理論の方が極大宇宙の理解に自然な尺度と遠近法を与えているということを次に示そう。
まず、天文学的距離は、光速度を媒介として時間で表示されていることは周知の事柄である。そこでは、文字どおりc=1とする尺度が自然なのである。さらに、我々は、相対性理論でいう過去の光円錐上の領域(t<0, ds=0)に直観的な意味を与えることができる。すなわち、過去の光円錐とは、我々が夜空を見上げたときに我々の周囲に広がっている「時間の奥行きをもった」三次元空間として解釈できる。天文学者が観測している天体は、我々の地球時間を基準にしたその都度の現在(dt=0)の宇宙の姿なのではない。例えば、冥王星は5時間前の、ケンタウロス座のαは4年前の、アンドロメダ星雲は150万年前のというように、過去に向かう時間的な奥行きをもった対象の姿を、今此処で見ているのである。このことは、古典物理学の時空概念に従うならば、「遠方の天体になればなるほど、それだけ遠い過去の宇宙の姿を我々に見せている」ということになろう。
しかし、「遠い」とか「近い」という語を、空間と時間の計量を切り離して考えているならば、それは、我々の基準系でのみ通用する考え方であることに注意しなければならない。 基準系の選択に依存しない四次元距離で測るならば、宇宙のどれほど遠方の、どれほど過去におきた出来事であっても、時間的または空間的な四次元距離の尺度において、我々のごく近傍にあるといわねばならない場合がある。我々が、例えば今日観測した超新星の爆発が、10万年前に10万光年はなれた遥か遠方で生起した出来事であったという場合、相対論的宇宙論の遠近法によれば、その出来事は、今此処と四次元的な距離において近接しており、昨日地上で我々の周辺で起きたどんな出来事よりも、我々に近いということができる。
過去の光円錐とは時間の奥行を持った三次元の空間である。それは、現在的直接性(presentational immediacy)をもって知覚されるのであり、ここで示されたような相対論的宇宙論の遠近法によれば、我々が見上げる夜空の星は、そのままで、ビッグバン以後の悠久の宇宙の歴史的過去を、今此処で直接に開示していることになろう。
















