マグニチュードの計算式:
Eは、地震が発するエネルギーの大きさ(単位:ジュール)
Mは、マグニチュード
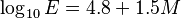
これをLog計算する。
定数4.8は無視する。
マグニチュード(M)を1とする
E=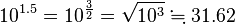
マグニチュードが1違うと、そのエネルギーは、32倍違う。
従って、マグニチュード6.5と、マグニチュード7.5では、32倍違う
Mが2違うと、1064倍違うことになる。
4月14日は、マグニチュード6.5の前震
4月16日は、マグニチュード7.3(14日のM+0.8)の本震となった。
この数式に当てはめると、10^(1.5×0.8)=10^(1.2)=15.85=約16倍
前震と比べると16倍の大きさであったことになります。
本震の大きさがお分かり頂けたかと思います。
4月14日の前震で弱った構造物、土壌に、4月16日未明に16倍の大きさで叩きのめされたことになります。
従って、多くの建物の崩壊、山崩れが生じたと考えます。
(追記)4月17日の新聞では、次の記事がでていた
阪神大震災のマグニチュードは、6.9だそうです。
今回の熊本のマグニチュードは、7.0です。
その大きさは、10^(1.5×0.1)=10^0.15=1.412=1.4倍となります。
計算式ではあっている。
しかし、過去の阪神大震災(気象庁)では、マグニチュード7.3となっています。
http://www.data.jma.go.jp/svd/eqev/data/1995_01_17_hyogonanbu/
どれが正しいのか?
阪神大震災のマグニチュードを7.3とすると、10^0.45=2.8となり、阪神大震災より2.8分の1、小さかったことになります。
なお、震度7以上の地震は、次のとおり。
1995/1/17 阪神淡路大震災 M7.3
2004/10/23 新潟県中越地震 M6.8
2011/3/11 東日本大震災 M9.0
今回の熊本地震で4回目である。
マグニチュードでは、阪神大震災並みであった。
マグニチュードは、エネルギーの大きさで、震度は、地表での揺れの基準である。
大きなマグニチュードでも、遠くで発生すれば、または、地下深くで発生すれば、震度は大きくない。
阪神淡路大震災、新潟県中越地震、今回の熊本地震は、活断層が動いた直下型で、深度が浅かったので、大きく揺れて、被害も大きかった。
閑話:
地震ランキングは、ここを参照:
http://homepage2.nifty.com/GmaGDW/grw/wdr/wdr007.html#001
東日本大震災は、世界の大地震で、2番目に大きい地震でした。
余震が収まることを祈りながら、大地震への備えの必要性を感じます。
我が家も、不足している物については、追加し備えます。