
私たちの思考や感性を司る脳は全体で千数百億個もの「神経細胞(生体ニューロン)」から構成されています。人間の感性を数値化する必要があります。この理論の出発点は神経細胞を数理モデル化した人工ニューロン・モデルであり、究極的には脳の機能をコンピュータ上にモデルとして再現しようとしているものです。
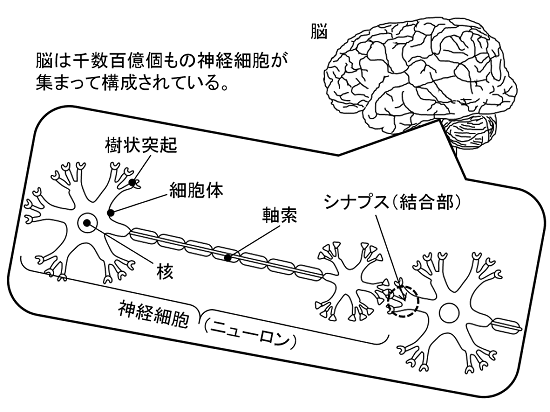
生体ニューロン間の信号伝達のプロセスは、(1)前段のニューロンのシナプスから発せられたパルスを樹状突起で受ける、(2)パルスの持つ電気によって細胞体の膜電位が上昇する、(3)膜電位がその生体ニューロン特有の閾値電圧を超えると細胞体内部で新たなパルスが発生する、(4)このパルスが軸索を通じて出力される、(5)シナプスを通じて後段の生体ニューロンに向けて放射される、というものです。
この生体ニューロンの機能を模式的に表現したものが次の図に示すモデルです。これを人工ニューロンと言います。一般的には「人工」を省略して「ニューロン」と呼んでいます。

細胞体に相当するユニットを中心に、樹状突起に相当する入力、シナプスに相当する結合荷重、軸索に相当する出力から構成されます。前段の人工ニューロンから出力される多くの信号が、この人工ニューロンに入力されます。これらの入力値は各々、結合荷重に応じて重み付けられてユニット内で数的処理が行われます。その結果となる値が、後段の人工ニューロンに向けて出力されます。
続いて、この人工ニューロンの数式化を考えます。次に示すように入力をx1~xn、線形結合をw1~wn、閾値をθ、出力をyとします。

また、入力信号と線形荷重の積の総和をネット値と呼びます。ニューロンの膜電位が閾値電圧を超えるとパルスを発生する現象を、モデル上はネット値が閾値を超える場合にy=1が出力される事で表現します。ここでシグモイド関数が登場します。

このようなニューロンのモデルを幾つもつなげてネットワーク状に接続した構造を、(人工)ニューラルネットワークと言います。脳の構造を単純化して、その機能のモデリングを図ったもので、様々な分野におけるパターン学習による推定という形での応用が可能です。

ニューラルネットワークは、入力変数と出力変数のデータベースを学習することで、入出力関係を再現するモデルとして最適化が可能です。
この学習の流れは、(1)入力値をニューラルネットワークに与える、(2)その入力値を基にニューラルネットワークが予測値を計算する、(3)予測値と教師データ(正解値)を比較して誤差を評価する、(4)得られた誤差を基に、ニューラルネットワーク内の結合荷重(シナプス係数)の値を逐次修正する、というプロセスを繰り返すものです。このプロセスを繰り返すことにより、ニューラルネットワーク全体としての最適化が図られていきます。

















