午前中は片道1.5hをかけてコーチング研修に参加してきました。今は戻ってきて束の間の休憩。もうすぐ、学習塾の方へ出勤(こちらは片道15min.)です。
「なんか梅雨に入ったって言うけれど・・・雨降らないね・・・」
「もう梅雨明けして夏になったんじゃない!?」
これは私もあちこちでよく聞くフレーズです。学習塾の教室でも、コーチングの研修でも、挨拶代わりの定番フレーズにさえ、なっているようです。このフレーズを聞いても、私はただ・・・黙って聞いています。
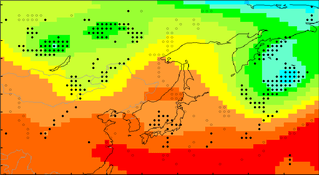
第1図.上空500hPa面ジオポテンシャル高度(2012年06月28日21時)
※青→緑→黄→赤の順にz500の高度は高くなります。日本の南の赤い部分が5880mに相当しています。図中●はトラフ域、○はリッジ域を表しています。
日本の南には夏の高気圧を象徴する5880mの太平洋高気圧が既にスタンバイしています。これが日本を広く覆うようになれば、北陸~東北でも梅雨明けの便りとなるのですが、現段階では東北~北陸の梅雨明けはまだまだのようです。
北海道の北西に目を移しますと、〇が縦に並び、オレンジ色の領域が北に向かって突き出ている様子が見られます。これはリッジですね。梅雨前線は北のオホーツク海高気圧と南の太平洋高気圧の覇権争いの中で生じるわけですが、北日本の場合、オホーツク海高気圧の勢力が非常に強く、その影響がドミナントだった事が判ります。
実際の梅雨前線は西日本にしつこく居座る傾向があったのもこのためです。北と南の高気圧帯に挟まれるように、西日本を中心に●が集まっています。これは上空のトラフ(気圧の谷)を表しています。この付近に低気圧があるという事です。
「なんか梅雨に入ったって言うけれど・・・雨降らないね・・・」
「もう梅雨明けして夏になったんじゃない!?」
これは私があちこちでよく聞くフレーズです。
これが社内では・・・
「なんか梅雨に入ったって言うけれど・・・雨降らないね・・・」
「こんな調子だと・・・なんか後がコワイですね・・・。」
に変わります。
別に具体的な予報を行った上での発言ではありません。梅雨なのにここまで雨が降らない、という事は、後で帳尻を合わせるような反動が来るのではないか・・・という憶測です。この発言は、あくまでも予報ではありません。
但し、根拠のない憶測ではありません。新潟県内を例にとると、月別の平均降水量の傾向は次のようになります。
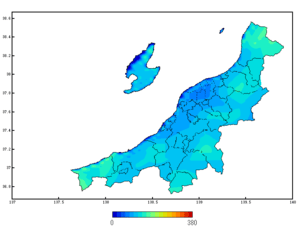
第2図.5月の平均降水量分布(新潟県内のみ)
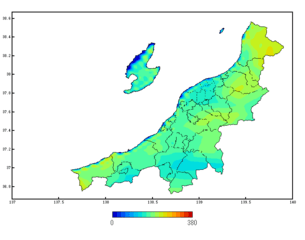
第3図.6月の平均降水量分布(新潟県内のみ)
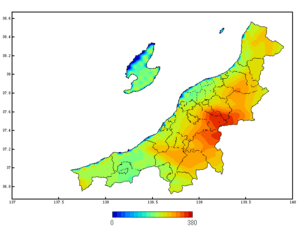
第4図.7月の平均降水量分布(新潟県内のみ)
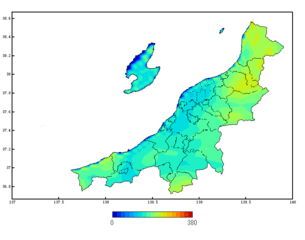
第5図.8月の平均降水量分布(新潟県内のみ)
梅雨入りする6月よりも、梅雨明けする7月の方が降水量は多いのです。梅雨前線が北上し、県内に最接近するのはたいてい梅雨の末期です。昨年の7月の終わりも凄まじい豪雨に見舞われ、長岡花火の開催も危ぶまれたほどです。
つまり、北国にとって「魔の月」は7月なのです。
「なんか梅雨に入ったって言うけれど・・・雨降らないね・・・」
「もう梅雨明けして夏になったんじゃない!?」
・・・騙されてはいけません。ヤツはこれからやってきます・・・。
さて、もう一杯コーヒー飲んだら、出かけるか・・・。
「なんか梅雨に入ったって言うけれど・・・雨降らないね・・・」
「もう梅雨明けして夏になったんじゃない!?」
これは私もあちこちでよく聞くフレーズです。学習塾の教室でも、コーチングの研修でも、挨拶代わりの定番フレーズにさえ、なっているようです。このフレーズを聞いても、私はただ・・・黙って聞いています。

第1図.上空500hPa面ジオポテンシャル高度(2012年06月28日21時)
※青→緑→黄→赤の順にz500の高度は高くなります。日本の南の赤い部分が5880mに相当しています。図中●はトラフ域、○はリッジ域を表しています。
日本の南には夏の高気圧を象徴する5880mの太平洋高気圧が既にスタンバイしています。これが日本を広く覆うようになれば、北陸~東北でも梅雨明けの便りとなるのですが、現段階では東北~北陸の梅雨明けはまだまだのようです。
北海道の北西に目を移しますと、〇が縦に並び、オレンジ色の領域が北に向かって突き出ている様子が見られます。これはリッジですね。梅雨前線は北のオホーツク海高気圧と南の太平洋高気圧の覇権争いの中で生じるわけですが、北日本の場合、オホーツク海高気圧の勢力が非常に強く、その影響がドミナントだった事が判ります。
実際の梅雨前線は西日本にしつこく居座る傾向があったのもこのためです。北と南の高気圧帯に挟まれるように、西日本を中心に●が集まっています。これは上空のトラフ(気圧の谷)を表しています。この付近に低気圧があるという事です。
「なんか梅雨に入ったって言うけれど・・・雨降らないね・・・」
「もう梅雨明けして夏になったんじゃない!?」
これは私があちこちでよく聞くフレーズです。
これが社内では・・・
「なんか梅雨に入ったって言うけれど・・・雨降らないね・・・」
「こんな調子だと・・・なんか後がコワイですね・・・。」
に変わります。
別に具体的な予報を行った上での発言ではありません。梅雨なのにここまで雨が降らない、という事は、後で帳尻を合わせるような反動が来るのではないか・・・という憶測です。この発言は、あくまでも予報ではありません。
但し、根拠のない憶測ではありません。新潟県内を例にとると、月別の平均降水量の傾向は次のようになります。

第2図.5月の平均降水量分布(新潟県内のみ)

第3図.6月の平均降水量分布(新潟県内のみ)

第4図.7月の平均降水量分布(新潟県内のみ)

第5図.8月の平均降水量分布(新潟県内のみ)
梅雨入りする6月よりも、梅雨明けする7月の方が降水量は多いのです。梅雨前線が北上し、県内に最接近するのはたいてい梅雨の末期です。昨年の7月の終わりも凄まじい豪雨に見舞われ、長岡花火の開催も危ぶまれたほどです。
つまり、北国にとって「魔の月」は7月なのです。
「なんか梅雨に入ったって言うけれど・・・雨降らないね・・・」
「もう梅雨明けして夏になったんじゃない!?」
・・・騙されてはいけません。ヤツはこれからやってきます・・・。
さて、もう一杯コーヒー飲んだら、出かけるか・・・。