円筒座標系の熱流体方程式と熱ロスビー波

　大気大循環に伴う波動発生のメカニズムは、例えば北極と見做した中心を氷等で冷やした回転二重円筒間の流れ(熱ロスビー波)で模擬される事が知られています。そこで今回はこの実験に倣って、半径方向に温度勾配を与えられながら、一定の回転角速度で回転し続ける二重円筒形状容器を考え、その内部に充填された試験流体の熱流動の数値シミュレーションを独自に開発して波動の再現を試みました。

　解析に用いる基礎方程式は、次のような連立非線形偏微分方程式です。

【円筒座標系で表現される強制対流のNavier-Stokes方程式】
　（∂ｖ/∂ｔ）＋（ｖ・∇）ｖ＋２ω×ｖ＝－∇ｐ＋（１/Ｒｅ）∇²ｖ＋（Ｇｒ/Ｒｅ²）Ｔδ_i3

【円筒座標系で表現される熱エネルギー方程式】
　（∂Ｔ/∂ｔ）＋（ｖ・∇）Ｔ＋２ω×ｖ＝（１/Ｐｒ・Ｒｅ）∇²Ｔ

【微分演算子とベクトル】
　∇＝（∂/∂ｒ）＋（∂/ｒ∂θ）＋（∂/∂ｚ），ｖ＝（ｖ_ｒ，ｖ_θ，ｖ_ｚ）

　ここで、ｖ_ｒ、ｖ_θ、ｖ_ｚは各々半径方向、円周方向、鉛直方向の速度成分であり、ｐ、Ｔは各々圧力、温度である。また、Ｒｅ、Ｇｒ、Ｐｒは各々Reynolds数、Grashof数、Prandtl数である。

　今回想定する実験装置(数値モデル)の概要は次のようなイメージです。

　

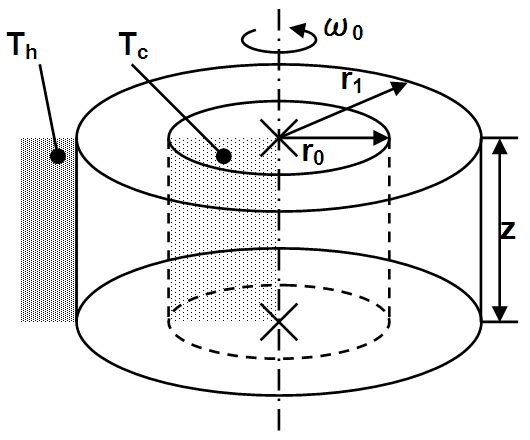
　実験装置は半径r_０及びr_１の二重円筒で構成されており、内側の円筒を冷源T_ｃとし、外側の容器内に試験流体が充填されるものとします。更に外側の容器の周囲には一様な熱源T_ｈが分布しているものとします。

　そして、この実験装置全体を一定角速度ω_０で反時計回りに回転させます。

　ここで、寸法はΔr= r_１－r_０を基準として、r_０＝Δr、r_１＝2Δr,z＝Δr/2に設定しました。 従って、Reynolds数は試験流体の動粘度係数νを用いてRe=ω_０(Δr)^２ /νで表され、Grashof数は体膨張率β_０、重力加速度gを用いる事により、Gr＝gβ_０(T_ｈ－T_ｃ)×(Δr)^３ /ν^２で表されます。

　続いて、初期条件・境界条件の概要は次のような形です。

　壁面摩擦を受けない場合v_θは単純にv_θ＝ｒωに従うため、最外周で極大となります。しかし、実際には壁面摩擦を受けるので内壁面および最外周壁面上ではθ方向の速度は0にならなければいけません。初期状態においてはこの境界条件を満足する発達した流れを想定し、v_θ(r)はr方向に放物状の速度分布を成すものと仮定します。

　また、温度に関する境界条件は、内側円筒に相当するr≦r_０は冷源であるため T=T_ｃ、最外周壁面に相当するr=r_１は熱源であるため T=T_ｈです。初期条件は、r_０≦r≦r_０+Δr/2では試験流体が冷却されているため T=T_０とし、r_０+Δr/2≦r≦r_１では試験流体が加熱されているためT=T_０＋ΔTとします。

　今回はGr＝1.0×10^２,Re＝3.0×10^２,Pr＝0.71の条件を設定し,３次元熱流動の数値シミュレーションを行いました。その結果は・・・。

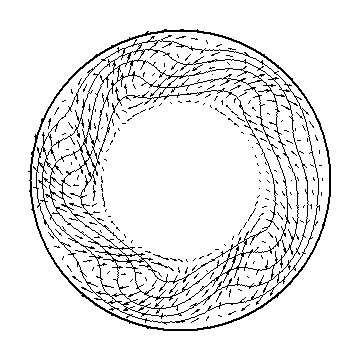
　こちらは、円筒の高さの半分に相当するZ=Δr/4における水平面上の温度と流れの様子を解析した結果です。波数5の熱ロスビー波が形成されているのが分かります。波が中心に向かって盛り上がる位相(リッジ)の右側では時計回り、左側では反時計周りの渦が形成されています。一方、中心から遠ざかる位相(トラフ)ではこれとは反対の構造になっています。

　続いてこちらは、この水平面上における鉛直渦度ζと流れの様子を解析した結果です。

　正渦度域(ζ>0)と負渦度域(ζ<0)が交互に形成されている事が分かります。従って、トラフの右側(リッジの左側)では正渦度循環、リッジの右側(トラフの左側)では負渦度循環が形成される現象が再現されました。

確かなニーズはどこにある？

　現在では、メッシュ状に分割されたエリア単位の細かい予報が簡単に「無料で」見ることができる時代です。

　レジャースポットのピンポイント予報などはもちろん、ピンポイント予報を基にした来客数や品別売上の予測（ウェザー・マーチャン・ダイジング）や健康面への影響の予測（健康天気予報）、工事現場の詳細な雨・風・雷の予測情報等のサービスも次々に実用化され、都市部を中心に大手の気象情報会社によって既に事業化されています。

　また、気象予報士の資格を取得してメディアデビューを果たすケースも少なくありません。「ザイアンスの法則」の視点で考えると、メディアに登場するウェザーキャスターはある意味「最強」です。なぜなら、彼らは「自分自身」が既に「ブランド」であり「付加価値」になり得るのですから。まさに理想的なセルフ・ブランディングの実現ですね。

　そのメリットを最大限に活かした事例として、ウェザーキャスターを多く抱える気象情報会社では、好きな気象予報士（≒ウェザーキャスター）を指名して自分のためだけの独自の天気予報をリクエストできるサービスを提供しています。お目当ての気象予報士から自分だけのためのメッセージも送られてくるとか？当たり前ですが、もちろん有料です。

　以上のような「強者」に対して、私は残念ながら「弱者」の立場。

　そこで、「ランチェスター戦略」(＝弱者の戦略)の考え方が浮上します。所謂「一般的な広く大衆受けするような」気象情報ではなく、特別な用途に限定された「ホンの一握りの人のための」気象情報を生み出していく（＝ニッチ市場を目指す）方向に発想を切り替えて行かなければなりません。

　そもそも、「気象庁やメディア等の無料の天気予報」と「気象情報会社が独自に配信する天気予報」は何が違うのかと言うと、一番の違いは、前者が「プロダクト・アウト」であるのに対して後者は「マーケット・イン」である事ではないかと思います。

　話は変わりますが、私は中学時代、吹奏楽部に所属してトランペットを吹いていました。そこで気になったのが、トランペット一台当りのお値段。YAMAHAのトランペットについては、こちらのサイトに掲載されています。

　安いものは￥55,650～高いものだと￥409,500。

　この価格帯の広さ・・・一体、何が違うのでしょうか？パッと見た感じでは、さっぱりわかりません。どれでもちゃんと吹けば音が出るんでしょ？しかし「その音色」や「吹奏感」がやはり違うようなのです・・・が、私にはわかりません。所詮、私はその程度のレベルです。安い物は工場の生産ラインで作られるが、高級品は職人の手作りだ、と聞いたことがあります。「違いが分かる」というのは相当のレベルの奏者であるという事。「分かる人には分かる」が、「たいていの人」には理解されない。しかし、そこに「確かな付加価値」が存在するのです。

　この「確かな付加価値」を求める「潜在的なニーズ」を如何に掘り起こすか・・・。それが問題だなあ。

コーチングスキル講座(中級)を受講しました。

　本日、４回目の研修が無事終了しました・・・一区切りです。

　私が受講したのは「コーチングスキル講座(中級)」です。５月の単発講座「心を結ぶ会話術」(≒導入編１回)に始まり、コーチングスキル講座の初級講座(４回)、中級講座(４回)とこれまで計９回を受講してきました。

　私が初めて「コーチング」と出会ったのは、2006年05月27日に受講した「心を結ぶ会話術」。これは新潟の地に移って最初に受講した公開講座でもあったので、今でも鮮明に覚えています。当時(2006年)の講師は、コーチングを手掛ける会社を起業した女性の方でした。何かすごいエネルギーに満ち溢れ、その瞳にもすごい力を感じました。

　この時の事はこの日のブログにもしっかりと書き残していました。

　この講座には、一つ「思い出」があります。講座の始まると、受講者は一通り「自己紹介」をするように言われました。名前と住んでいる所、そしてどんな仕事をしているのか・・・この時の私は、ある方に誘われる形で、とある情報ベンチャー企業の気象事業に関わっていましたので、自分の仕事について「天気予報に関する仕事に従事しています」と言った所・・・まるで何かに反応したように、すかさず「ちょっと聞いて良いですか？」と、天気に関する素朴な疑問を投げかけられました。

　これまで様々な研修や講座を受講してきましたが、講師からの「(天気に関する)逆質問」はこれまで「この１回」でした。その内容も、私にとってはとても「斬新な視点」からのものだったので、今でも覚えています。いつの日にか、私もどこかで使わせてもらおう・・・と思っているのでした。

　あのまま後続のコーチングスキルを受講する道もあったのですが・・・「受講するのは(当時の)自分にはまだ早い。然るべき段階に至った時に再びその時が来るだろう・・・」と(本能的に)感じたので、結局それっきりになっていましたf(-_-;)。


　それからもう、６年・・・この間に、私も実に色々な事がありました・・・(-_-)・・・(しみじみ)。今ではこれらの講座は、社長を支えるスタッフさんに委ねられています。


　この会社の公式メールマガジンも拝読していますが、そのメルマガを執筆しているのもこのスタッフさん(＝今回の一連の講師を務めて下さった方です)。御自身もかつて色々と悩んでいた時に「コーチング」に導かれ、その扉を開いて「コーチ」として活躍するまでのエピソードが綴られており、引きこまれるようにバックナンバーを何度も何度も読み返しました。様々なエピソードを通じて、自らの可能性を次々と開拓していく展開は、読者である私にも一筋の希望を与えてくれるものでした(どこかで自らの未来を重ね合わせているのかもしれません)。

　その一方で社長自身もブログを書かれており、その痛快なタッチで語られるエピソードの中にも多くの学びが含まれていました。コーチングのスキルも然ることながら、御二人の生き様やその活躍ぶりにも学ぶものがあると感じています。

　これまで９回（６年前の１回を加えると１０回）の研修を通じて、私の中で「コミュニケーション」に対する考え方が少しずつ変わってきました。そして、「コミュニケーション」という「現象」を理論的に俯瞰できるような視点が培われていくのを感じました。

　コミュニケーションのスタイルは人ぞれぞれであって良い・・・そう思えた時、長年私を苦しめていた既成(寄生)概念が崩れ落ちていくのを感じました。コミュニケーションのスタイルを確立するにあたっての基礎理論が、きっと「コーチング」の中にあるのだろう・・・と感じ始めています。

　まだ、私の模索は続いています。ひょっとしたら終わる事は無いのかも知れません・・・。まあ、「朝に道を聞かば、夕べに死すとも可なり」という言葉もある位ですから・・・f(^^;)


写真は萬代橋からから臨む信濃川

物理の授業で何を学ぶか？ 数学と物理と「モデル」の関係

局地気象のシミュレーションで格闘中・・・解析手法に悩み、苦しみ悶えている・・・(笑)


　これまでの人生を振り返って、「数学は得意だけど、物理は苦手」と言う人には多く出会ってきましたが、「物理は得意だけど、数学は苦手」と言う人は・・・正直、会ったことがありません。むしろ、物理が得意な人は数学も得意（もしくは好き）と言う人ばかりだった・・・と思います。

　一見、似た者同士のこの両者の違いはどこにあるのか・・・ふと、考えてみたことがあります。大学の理学部以上で学ぶ、または研究する数学や物理学の事はわかりませんが、高校生～大学教養レベルに限定して言えば、 「数学」は（既にある）公式や定理を縦横無尽に使いこなす事が求められるのに対して、 「物理」は（既にある）基本的な法則や公式を縦横無尽に使いこなして、新たな公式や方程式を組み立てる事が求められます。「物理」の問題は公式や方程式を組み立ててしまえば、後は「数学」の問題に帰着されるのです。つまり、両者の差は（問題として）与えられた現象について、新たな公式や方程式を「組み立てる」事にあるのではないか、と思えるのです。

　物理の問題は、基本的な物理現象を幾つも組み合わせた現象をテーマに出題されるため、どのような基本的な現象が、どのように組み合わされているのかを理解し、認識した上で、それぞれの基本現象の公式を組み合わせて、出題されている現象に見合った方程式を構築する・・・と言う高度な（ある意味、面倒臭い）プロセスを経る必要があります。なるほどこの部分に苦手意識を持つ・・・と言う事でしょうか。その一方で、まさにこのプロセスこそが「醍醐味」と感じる人もいるわけですね。

　物理の教科書を開くと公式の数も膨大です。これを全部、暗記するのは・・・無理だよなあ・・・と尻込みしてしまうケースも少なくありません。しかし、我が身を振り返ってみると、自分が使っている公式は・・・実はその膨大な中のごく一部に過ぎない事に気づきます。必要最小限の公式を覚えておけば、後は必要に応じて、その都度「公式」を組み立てる事が出来るからです。多くの物理の先生が、公式を覚えるのではなく、その公式がどのような法則や考え方から導かれるかを学ぶ事の重要性を指摘されています。

　結局、基本的な法則や公式に則って、どのように現象を理解し認識してゆけば良いのか ・・・その「思考法＝ものの見方・考え方」を学ぶことがすなわち「物理」の勉強なのだ、と今更ながら実感しています。そして、現象やその構造・メカニズムに対する「自分なりの理解や認識」を具現化（表現）したものが「（解析）モデル」なのです。「物理の問題を解く」と言うことはすなわち、対象となる現象を「解析モデル」の形で表現し、考える事に他なりません。

　これまで学んできた機械工学も、バイオメカニクスも、エレクトロニクスも、建設・土木工学も、そして気象学も・・・対象とする現象や応用する分野は異なりますが、その対象となる現象を物理学の法則に照らし合わせて、その本質をモデル化し、数学と言う言語を用いて表現し、後はそれらをどのように応用していくか・・・につながっていくものです。

　現在、私が挑んでいる分野も複雑な局地気象のメカニズムやその構造を一旦「簡単な模型のイメージ」に落とし込んでから、物理学の法則に照らし合わせて、その本質をモデル化し、方程式や拘束条件を構築し、これをコンピューターで計算するというもの。または、局地気象のファンクション（機能）だけに着目し、これを「簡単な計算式」で表現して、コンピューターで計算するというもの。

　「効果的な質問を投げかけることで、相手の思考を促す事が出来る」とは、先日のコーチングの研修で学んだ事。

　複雑な現象を「簡単な模型のイメージ」に落とし込む際は、一つ一つの特徴についてこの本質は何なのか、それはどのように解釈・理解・表現すればよいのか、絶えず（無意識の内に）自らに問いかけています。結局は、目の前の現象やその本質を「どのように理解したか？」と言う究極の問いかけに対して、「自分なりの考え方」を構築し「自分なりの答え」を導き出そうとする営みなのです。

　質問力・・・鍛えないと・・・だな・・・。