ガス事業を想定した収益予測の試み

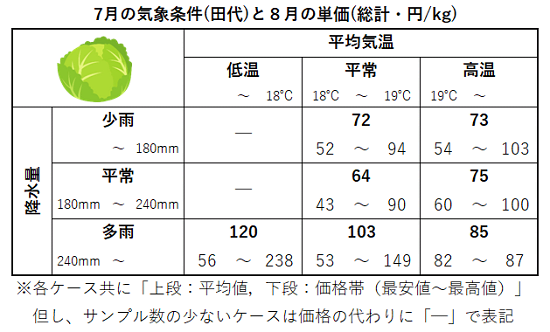
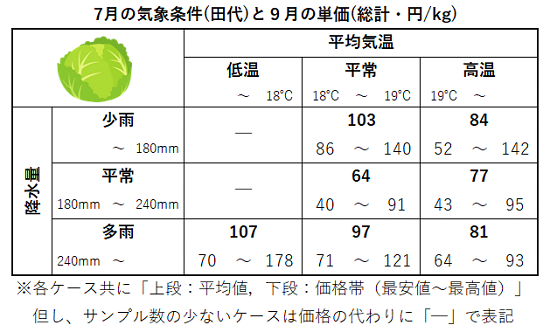
 最近まで読んでいた「天候リスクマネジメントへのアンサンブル予報の活用に関する調査」、「企業の天候リスクと中長期気象予報の活用に関する調査」の報告書を参考に、気象条件の事業収益に与える影響を解析してみました。

 今回は、都市ガスの製造・販売等を行う事業者（企業）を想定し、収益予測のシミュレーションを試みました。言うまでもなく、実際の企業活動や収益発生のプロセスはとても複雑です。このプロセスを簡易モデル化するために、次のような５つの仮定を設けました。そしてこれらの過程に基づく予測モデルを構築し、理想化されたケースでシミュレーションを行います。


（仮定１）売上はガス販売、ガス関連工事、ガス関連器具他の３種類から構成される。また、ガス販売の内訳は家庭用・商業用・工業用・その他用の４種類に分類される。

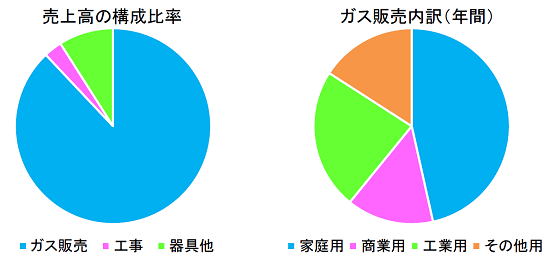
 ここで、売上高の構成比率は、ガス販売が約８８％、工事が約３％、器具他が約９％を占めています。また、ガス販売の内訳は、家庭用が約４５％、工業用が約２４％、商業用が約１５％、その他用が約１６％を占めています。


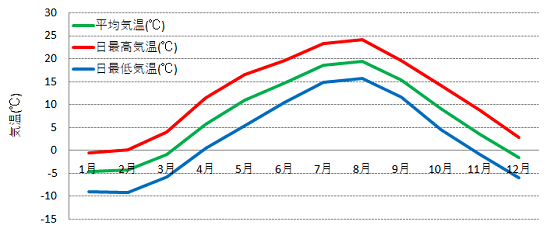
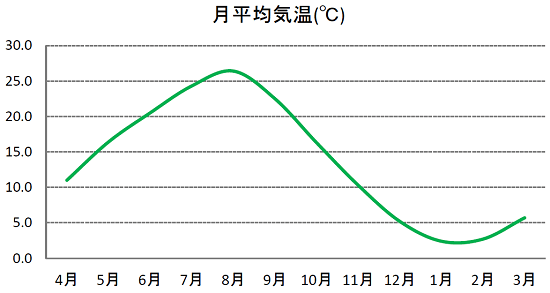
（仮定２）ガス販売量は気温（月平均気温）の関数（２次関数）として表現できるものとする（なお、企業の事業年度は４月１日から翌年３月末とする）。

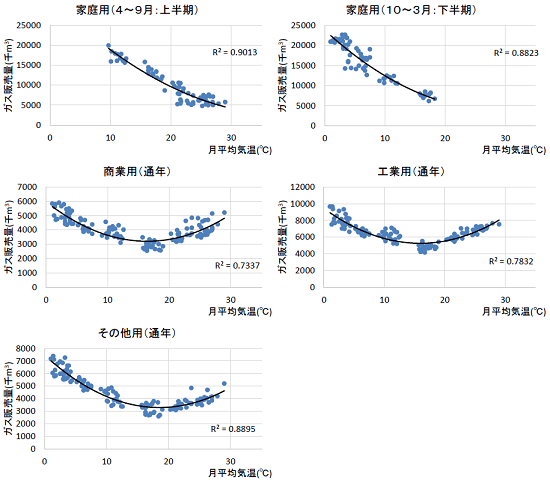
 月平均気温とガス販売量の散布図をベースに相関を求めます。ここでは、ガス販売量を月平均気温の２次関数としました。


（仮定３）ガス関連工事、ガス関連器具他の売上高、およびその他の収益（営業雑収益、営業外収益）の類は確率的に決まるものとする。また、特別収益は考慮しない。

（仮定４）売上の発生に要する原価・費用の類は、対応する売上高に比例し、その（売上高に対する）比率は確率的に決まるものとする。また、特別損失は考慮しない。

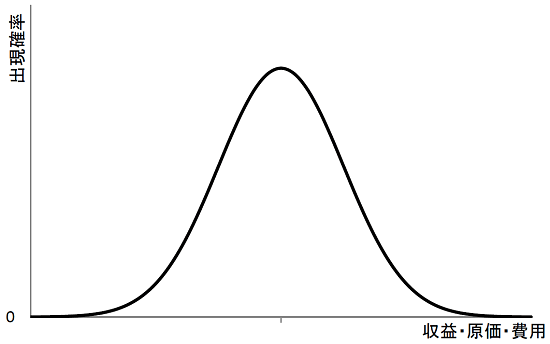
 ここで、確率変数（収益・原価・費用）は正規分布Ｎ（μ,σ）に従い、区間［μ－２σ,μ＋２σ］の範囲で変動するものと仮定しました。


（仮定５）法人税等（税金を全て引っ包める）は、税引前当期純利益の関数として表現できるものとする。税引前当期純利益が０円以下の場合は定額とし、税引前当期純利益が０円を超える場合は一定の比率を加算するものとする。

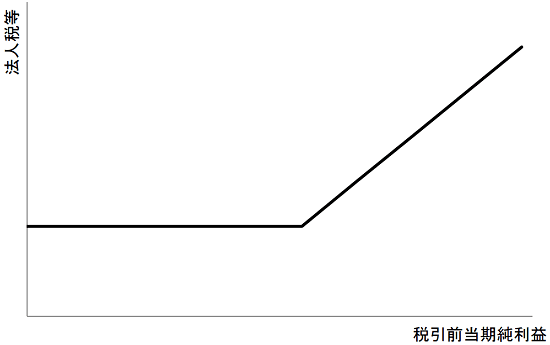
 税金は大きく分けて、利益に比例して（所得に応じて）課されるものと、利益に関わらず課されるものの合算と考えました。


 以上の仮定に基づき、次のようなフローで計算を実施します。左側が収入、右側が支出に対応します。中央が企業に残る利益です。なお、売上の中核を占めるガス販売売上高は気温の変動に左右されるので、この数値モデルは「気温変動型収益予測モデル」と言っても良いでしょう。数値計算にはモンテカルロ法を使用し、予想される「当期純利益」の確率分布を求めます。

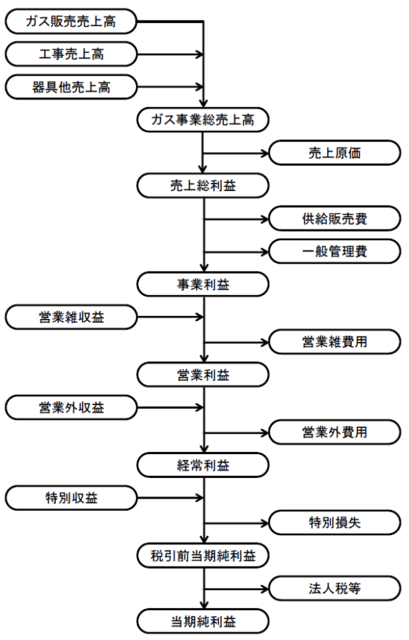
 早速、平年値ベースの気温の変動パターンを適用してシミュレーションを実施します。

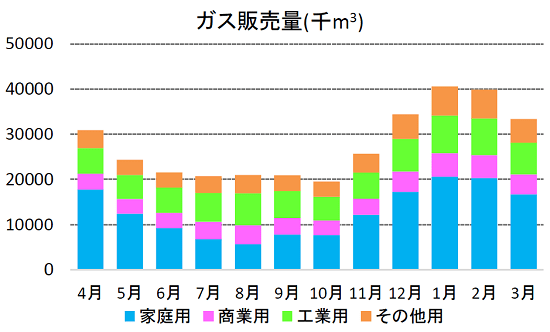
 この結果、月別のガス販売量はこのような形になりました。この企業モデルの場合、ガス販売量は夏の間は低い水準に留まる一方、冬になると大幅に増加する傾向が見られます。冬は家庭での暖房や温水の需要が高まるので、そのようなニーズを反映しているものと理解できます。

 そして、この場合の予想される当期純利益の分布はこのようになります。不確定要素（確率的に変動する要素）が多いため、バラツキが大きくなってます。この確率分布を基にして、さらに当期純利益の期待値やEaR(Earnings at Risk)を用いた評価を行う必要がありそうです。

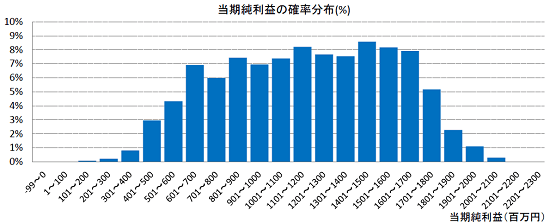
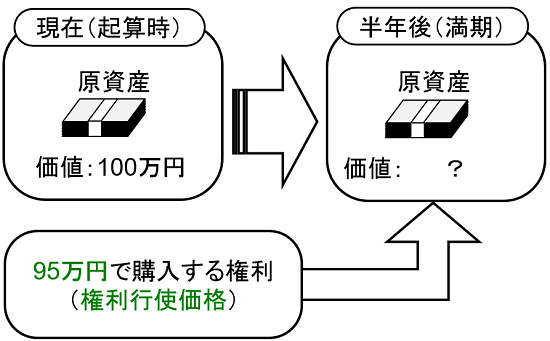
 ここで、EaR(Earnings at Risk)とは、ある確率（95%や99%）で予想される最低の「収益」の事です。似た概念としてVaR（Value at Risk）がありますが、こちらは「資産」を対象としています。

 様々な気温パターンについてシミュレーションを行い、（当期純利益の）期待値やEaRを比較することで、事業における天候リスクを浮き彫りにすると共に、天候デリバティブなどの対応策を検討することを目指していきたいです。

台風に備えるデリバティブ

 今年は色々な意味で顕著な気象現象が多発しているように感じます。台風の接近・通過の影響もいつになく大きいように感じています。そしてまた、新たな台風が近づいて来ています。

 このような状況を見ると、脳裏に浮かぶのが「台風リスクに対する保険」です。天候リスクに対する保険（金融派生商品）である「天候デリバティブ」の一つの種類として「台風に備えるデリバティブ」というものがあります。添付した図はその一例です。

 この事例のユーザは、８月～９月に台風の接近・通過の影響を受けやすく、これに伴い来客数の減少や減益のリスクを潜在的に抱えています。そこで、接近する台風の数に応じて補償金を受けとれるプランのデリバティブを契約しました。

 この台風の数の決定の仕方もユニークです。まずは、最寄の県庁所在地を中心とする半径１５０ｋｍの円内を「通過エリア」と定めています。そして、観測期間内（８月１日～９月３０日）の６１日間に、この通過エリアを（台風の中心が）通過する台風の数をカウントしていきます。１つでも台風が通過した時点で、補償金が発生します。

 今後は、このような形のリスクヘッジも普及することになるのかも知れません。もちろん、台風の接近・通過の確率（頻度）が高まると、掛け金（プレミアム）も上がります。それだけの掛け金をかけてでも、リスクヘッジのために契約（利用）すべきなのかどうかが思案の為所と思います。

 そもそも、天候デリバティブは「金融派生商品（デリバティブ）」の一種です。つまり、天候の変化（気象要素の変動）から派生する形で価値が変動する金融商品（デリバティブ商品）と言うことです。これを「保険」のような形で利用することが出来るのです。従って、一般的な「損害保険」とは似て非なるものです。

 ここで、気象要素（気象指標：インデックス）の変動やそこから派生する金融商品の価値の変動が確率的に起こるものと仮定して数学的に評価するのが金融工学の考え方です。

夏の暑さとキャベツの卸売価格

 この夏の猛暑の影響で、野菜の価格が高騰しているようです。そこで、夏の気象条件と夏秋キャベツの価格の傾向について調べてみました。今回、キャベツの入荷数量と単価については、1984～2017年における東京都中央卸売市場入荷分の月別の集計値を使用しました。

 まずは、東京都中央卸売市場に入荷されるキャベツについて、産地別の比率を月別で表してみます。

 この表からは、季節ごとの主な産地が判ります。11～3月（冬キャベツ）は愛知県・千葉県・神奈川県、4～6月（春キャベツ）は千葉県・神奈川県、そして7～10月（夏秋キャベツ）は群馬県・北海道・岩手県が各々主な生産地となっています。

 続いて、キャベツの入荷数量と単価の平均的な月次変動をグラフに表してみます。これは、東京都中央卸売市場におけるキャベツの入荷数量と単価の平均的な動きを表したものです。1984～2017年の各月毎の平均値を求めてグラフ化しました。

 冬（1～4月）は単価が100円/kgと高めで推移しますが、その他の時期は概ね70～90円/kgで推移しています。また、入荷数量は春（3～5月）に18～19千ｔと一時的に増加しますが、その他の季節は14～16千ｔで緩やかに変動するようです。但し、これは平均的な動きです。

 もう一つ注目したいのは、数量の極大値が４月なのに対して、単価の極小値は６月に現れていることです。需給均衡の観点からみると、供給（数量）と価格は反比例の関係にある筈です。つまり、４月の数量増加の影響が、６月の価格下落につながっていると見ることができます。数量の増減の変動が２か月後の単価の変動に反映されると考えて良いものか、判断に迷います。

 続いて、夏秋キャベツの生産地の気候について検討しましょう。夏秋キャベツの主な生産地として群馬県に注目します。8～9月のキャベツの入荷量では75～76%のシェアを誇っています。特に嬬恋村がキャベツの主な生産地として有名です。

 さて、キャベツは冷涼な気候を好む一方、耐寒性にも優れています。このため、露地栽培の生育適温は15～20℃と言われています。嬬恋村の気象の変化は田代アメダスで観測されています。月別の平均気温（平年値）をグラフに表してみます。

 平均気温を見ると、6～9月がこの生育気温の範囲内となっています。標高も1230mと高いので、気温は余り上がらず、夏秋キャベツの栽培に適していると考えられます。

 気温に続いて降水量も見てみましょう。太平洋側の地域という事もあり、冬の降水量が少なく、夏から秋にかけての降水量が多い傾向が表れています。

 ここからは、7月の気象条件と8～9月の（卸売）単価の傾向を検討します。

 ここでは、気象条件を「気温と降水量の組合せ」として考えます。さらに、気温を「低温・平常・高温」、降水量を「少雨・平常・多雨」と各々３つのカテゴリーに分類し、３×３の計９種類のパターンに分けて考えます。

 その後、過去34年分のデータを基に、上記９種類のパターンに該当する年の８月または９月の単価の「平均値・最安値・最高値」を算出して、マトリクスの形に表します。

 なお、田代の７月の平年値は「平均気温：18.6℃、降水量：208.7mm」、また今年（2018年）７月の観測値は「平均気温：21.1℃、降水量：221.5mm」でした。

 ７月の気温・降水量共に平年並み（平常）であれば、８月の卸売価格（単価・1kg当たり）も43～90円の範囲で変動・平均64円の水準にあると言えます。

 しかし、今年（2018年）は降水量は「平常」の範囲内となる一方、猛暑のため気温は「高温」の範囲内にあります。従って、1kg当たり60～100円の範囲で変動・平均75円の水準と、（平常時に比べて）２割ほど値上がりしやすい傾向にあります。

 同様に９月の単価の傾向も見てみましょう。

 ７月の気温・降水量共に平年並み（平常）であれば、９月の卸売価格（単価・1kg当たり）も40～91円の範囲で変動・平均64円の水準にあると言えます。

 しかし、今年（2018年）は降水量は「平常」、気温は「高温」に該当するため、1kg当たり43～95円の範囲で変動・平均77円の水準と、（平常時に比べて）２割ほど値上がりしやすい傾向にあります。

天気と博打の経済学

　北陸地方も、そろそろ梅雨入りが近づいてきました。

　梅雨前線の位置がちょっとズレるだけで、地域の空模様は大きく変わります。メディア用天気原稿の影の担当者としては、神経をすり減らすシーズンの到来です。日々の予報があたかも博打のように思えてくる心境です。

　最近、天気に保険を掛ける「天候デリバティブ」というのは、「天気と博打の経済学」のようなものだと感じています。保険もそもそも「不幸な状況に見舞われるかどうか」の博打です。金融商品も資産を賭けた博打です。（私の大好きな）時代劇でお馴染みの「丁半」も博打です。実は、原理的（数学的）には全て「確率過程」なのです。

　それでは、保険や金融商品とギャンブル（丁半など）の違いは何か、と言いますと、それは「実用性と娯楽性の違い」ではないかと思います。

　保険は「万が一への備え」、金融商品は「資産を増やす」という実用的な意味を持つのに対し、ギャンブルは単に娯楽・道楽としての意味合いが強いのです。どちらも本質的には「確率論」の話ですが、人間との関わり方やその意味合いに応じて、実用的であったり、娯楽であったりするのです。

　また、保険や金融商品は、エビデンスを基に設計された（実用的な）商品です。このエビデンスを与えているのが、数学や物理学に基づく「金融工学」の理論です。直観とインスピレーションで、それこそ適当に「丁！」だの「半！」だのとやっているわけではありません。

　さて、「天候デリバティブ」は「天気の動き」を賭けています。言うなれば「天気を対象にした博打」になります。さらに、その結果として「経済的な見返り」を期待しています。それこそまさに「天気と博打の経済学」です。しかし、博打でありながら「天候リスクを定量的に評価」している興味深い研究対象です。

　ここ２ヶ月ほど天候デリバティブの勉強に取り組んでいました。確率的に変動する金融資産（原資産）を仮定して、そこから派生するデリバティブ商品（コール・オプション）の価値の変動をコンピューターで計算する手法を検討しておりました。

　これをベースに天候デリバティブのシミュレーションに発展させることを目指しておりますが、それは当分先の話になりそうです。

(p.s.)
　私は競馬・競輪・パチンコ・パチスロなどのギャンブルは嗜みません。興味があるのは、あくまで「確率論（数学）」の方です。念のため。

オプション・プレミアムの数値シミュレーション

 オプションとは、将来の一定期間に、約束した金額で金融商品（金融資産）を売ったり、買ったりする事ができる「権利」です。ある金融資産を例にとって考えてみましょう。

 この金融資産は最初の時点（起算時）で１００万円の資産価値を持っているものとします。

 この金融資産を「半年後に購入しよう」とした場合、幾らで購入できるでしょうか？・・・それは半年後にならないと判りません。しかし、早めに購入することを決めておかないと、他の投資家に先に購入されてしまうかもしれません。

 そこで、半年後に「９５万円」で購入する「権利」を、今の内に購入してしまうのです。この権利がオプションです。

 この時、売買対象の金融資産のことを「原資産」、半年後と言う時期のことを「満期」、９５万円という価格を「権利行使価格」または「ストライク」と言います。

 オプション取引の対象となる金融資産は、その資産価値（資産価格）が時々刻々と上下に激しく変動するします。このような資産を運用した場合、大きな利益を上げることも期待できる半面、元本割れを起こしてしまう危険性もはらんでいます。このような金融資産を「危険資産」と言います。

 危険資産を数理モデルで表現する際は、平均的な変動（トレンド）は安全資産に準じるものとして、さらに不規則に変動する成分（ノイズ）を考慮します。ここで、トレンドの利率をリターン（μ）、ノイズの変動の大きさをリスク、またはボラティリティ（σ）と言います。

 危険資産の利率は確率的に変動します。有名なブラック・ショールズモデルでは、その確率分布を「正規分布」と仮定しているのが特徴です。

 続いて、満期時の資産価格とオプションの取り扱いについて考えてみましょう。

 満期（半年後）の時点で、この原資産（金融資産）の価格が暴落して、９５万円を下回った場合、このオプションを「放棄」することで、損失を免れることができます。

 一方、満期（半年後）の時点で、原資産（金融資産）の価格が高騰して、９５万円を上回った場合は、このオプションを「行使」することで、差額分だけ利得が発生します。

 オプション取引を行う際は、予め「使用料」を支払う必要があります。このオプションの価格（価値）のことを「プレミアム」と言います。

 オプション取引に伴う利得は青のグラフで表されますが、実際には既にプレミアムを支払っている状態なので、実際の収支は青のグラフよりもプレミアム分だけ下にシフトした赤のグラフのようになります。

 プレミアムは、将来時点で見込める利得を、現在時点での価値に換算したものです。オプション取引では、原資産の価値が時間と共に変動しています。これに伴って、オプションの価値・プレミアムもまた、時間的に変動しています。

 このような原資産の価格やプレミアムの時間的な変動を数値シミュレーションで見てみましょう。

【 設定条件 】
 資産価格の初期値：S₀ ＝ 100[万円]
 リターン    ：μ ＝ 3[%/年]
 ボラティリティ ：σ ＝ 10[%]
 無リスク利子率 ：ｒ ＝ 3[%/年]
 時間間隔    ：Δt ＝ 1[日]
 積分期間    ：Ｔ ＝ 183[日]

 まずは原資産の価格変動です。

 今回は起算時点から満期までの価格変動のシナリオを2000パターン計算しています。183日間に渡る価格変動をグラフに重ねてみました。時間が経つにつれて、変動の幅が広がる様子が判ります。

 なお、確率微分方程式の数値解法はエクスプリシット法（時間積分）とモンテカルロ法（ランダム変動）を使用しています。また、乱数生成においてはフォン・ノイマンの棄却法を適用しています。

 続いて、満期時点での資産価値の予測を見てみましょう。2000パターンのシナリオを基に、満期時点での資産価値の分布をヒストグラムで表示してみます。

 満期時点における資産価格は確率的に決まりますが、その分布は正規分布に従う様子が判ります。そもそも資産価値の確率微分方程式が正規分布に従っているので、その性質が反映されたものと考えられます。

 そして、いよいよ「プレミアム」の時間的な変動です。

 プレミアムは各時点における資産価値S(t)と権利行使価格K、さらに無リスク利子率rを用いて計算します。

 プレミアムは「期待値」で表されるため、予め2000パターンの各々における決済額（利得）を計算し、その平均を求めます。この平均値に対し、無リスク利子率と時点（日数）から決まるディスカウント・ファクターを乗じることで、プレミアムとしています。

 プレミアムは時間の経過と共に増加していく傾向が表れています。細かい上下変動を伴っていますが、概ね安定的に右肩上がりとなっているようです。プレミアムの価値は原資産の価値から派生しているため、その変動の性質も危険資産に準じています。その様子も視覚的に理解することが出来ます。

確率微分方程式の数値解析

 株価などの危険資産の価格変動は、次のような確率微分方程式で記述されます。

 ここで、μはリターン、σはボラティリティ、ｚ(ｔ)は不規則に変動する成分（ノイズ）です。ノイズはブラウン運動に従うもの仮定し、その確率分布は正規分布として扱われます。

 今回はこの確率微分方程式の数値解析を試みました。数値積分はエクスプリシット法＆モンテカルロ法を採用し、ノイズは乱数で与えることを検討しました。

 一般的に乱数を発生させる場合、プログラミング言語で用意される関数を用いると一様分布に従う乱数が生成されます。しかし、今回のノイズは平均0、標準偏差σ(√Δt)の正規分布となるため、一様乱数ではありません。そこで、任意の確率分布に従う乱数を生成させる手法として、「フォン・ノイマンの棄却法」を用いました。

 計算結果の一例を掲載します。

【 設定条件 】
 資産価格の初期値：S₀ ＝ 1000[円]
 リターン    ：μ ＝ 0.1[%/年]
 ボラティリティ ：σ ＝ 20[%]
 時間間隔    ：Δt ＝ 1/365[年]
 積分期間    ：１[年]

 ※確率過程なので、同じ条件でも計算する度に結果が変わります。

ウェザー・クオンツ

　年末のこの時期、あちこちから「金払えー！」の便りが届きます。「（電気料金などの）請求書」や「（所属団体の）年会費」という類です。決して、怪しい話ではありません。ただ、この手続きを行うことで「年の瀬」を実感しております。

　「お金」に関する話のついでという事で・・・昨年から今年にかけては「金融工学」を勉強してきました。金融工学に対しては、（気候変動などに伴う）経済的なリスクを定量的に評価する手法として興味を抱いておりますが、その重要な担い手となる専門職「クオンツ」についても関心を持っています。もちろん、いまさら「気象予報士」から「クオンツ」に転職しようという話ではありません。むしろ、「クオンツ」という専門職が現れた背景に興味があります。

　さて、「クオンツ」とは、「数量的、定量的」を意味する単語「Quantitative」から派生した言葉です。高度な数学的手法を用いて様々な金融市場や投資戦略を分析したり、デリバティブなどの金融商品を設計・開発する専門家です。ある時は複雑な数式を操り、またある時はプログラミングを行ってコンピュータで計算シミュレーションを行います。その基本となるのは確率論や金融工学の理論です。

　クオンツの起源は、１９８０年代のアメリカでＮＡＳＡのロケット工学の分野に関わっていた科学者が金融分野に転身した事と言われています。彼らは、持ち前の数学や物理学の理論を金融の問題に応用して、金融工学の様々な数理モデルやデリバティブ取引などの理論を開発していきました。現在、金融工学の理論に物理学の理論が活かされているのは、この名残と言っても良いでしょう。例えば、有名なブラック・ショールズ方程式を導出するに際しては、熱伝導方程式を解く必要があります（この他にも別の方法もあるようですが）。

　改めて考えてみると、お金（経済学）の問題を解決するために、わざわざ物理学の方程式を解くというのも変な話です。しかし、そこが面白い所です。（畑違いの）経済学の問題に対して、科学者（数学者・物理学者・工学者）がその（異分野の）専門知識を使ってアプローチしているのですから。私が日々取り組んでいることも実は同じようなものだと気付いたのです。

　私はもともと「気象学」の専門ではありません。ちょっと大げさに言えば「工学者（工学屋）」です。それこそ畑違いの気象学の問題に対して、機械工学（主に熱流体工学）や情報工学（主に人工知能）の専門知識を使ってアプローチしているのです。気象に関するデータを「工学屋のやり方」で分析し、どローカルな気象の予測モデルを設計・開発しているわけです。言ってみれば「気象版クオンツ」もとい「ウェザー・クオンツ」みたいなものです。

　若かりし頃は、数学の授業を聴きながら「こんな数学を学んでも、社会の何に役に立つんかな～～」と思っておりましたが、いやいや・・・「めちゃくちゃ役に立ってるやん！！」と今更のように実感しております。

金融工学の天候リスクへの応用 ～天候デリバティブ～

 天候デリバティブとは、将来の気象の変化に対して「保険」を掛けることにより、そのリスクをヘッジする手段です。これは、契約時に設定された一定の気象条件が実現した場合（指定された気象要素が閾値を超えたことが観測された場合）に、その観測値（閾値からの差分）に応じた補償金が支払われる「金融商品」です（※厳密には保険商品ではありません）。

 契約の際には、利用者は「保険の掛け金」に相当する「プレミアム」を保険会社等に支払います。このプレミアムは、将来における天候の影響とその発生確率に基づく期待値を基に算出されるため、将来における天候リスクの経済効果の指標と理解することもできます。そこで、ここでは簡単な契約プラン例を挙げて、プレミアムの算出について考えてみたいと思います。

 この例は、降水日数を指標とするコール・オプション取引です。

 インデックス（気象指標）には、観測期間中（Δｔ）に観測点（Ａ地点）で日降水量がＰmm以上を観測した日数（降水日数）の合計値ｘを用い、その値がＫ_I日（ストライク＝閾値）を超えると補償金が発生する仕様となっています。ここで、単位支払額はインデックス１日当たりＣ_L円、支払限度額はｈ_max円です。

 インデックスと補償金の関係を表すと、次のグラフのようになります。

 インデックスｘがストライク（Ｋ_I日）に達していなければ、補償金ｈ(ｘ)は発生しません。しかし、インデックスがストライクを超える場合は、その超過分に応じて（１日当たりＣ_L円の割合で）補償金が増えて行きます。但し、最大補償はｈ_max円と定められています。

 過去の気象データを基に、観測期間中（Δｔ）に観測点（Ａ地点）における日降水量がＰmm以上を観測した日数ｘを集計し、横軸にインデックスｘ、縦軸にはインデックスの発生確率（過去の出現頻度）ｆ(ｘ)という形に書き直してみます。

 続いて、インデックスと発生する補償金の関係を考えてみます。

 上の２つのグラフを基に、インデックスｘと発生する補償金の期待値ｈ(ｘ)ｆ(ｘ)を求めてみます。

 補償金と出現確率の積の総和＝このグラフの面積が、天候リスクに伴う補償金の期待値となります。平均的に発生し得る補償金額に相当します。そして、この補償金はあくまで将来時点（満期）における価値なので、これを現在時点（契約時）の価値に換算します。この換算された金額を基にプレミアムが決まります。

 ここで、ｒ_Iは無リスク利子率、exp(－ｒ_IΔｔ)はディスカウント・ファクターです。

オプション取引とBlack-Scholesの公式

 オプションとは、将来の一定期間に、約束した金額で金融商品（金融資産）を売ったり、買ったりする事ができる「権利」です。

 例えば、『株Ａ（時価：１１０万円）を６か月後に、１００万円で購入するオプション（権利）を購入する』 事案を考えてみましょう。この時、株Ａのことを「原資産」、６か月後と言う時期のことを「満期」、１００万円という価格を「権利行使価格」または「ストライク」と言います。

 もし、満期・６か月後に原資産・Ａの株価が暴落して、時価５０万円になった場合、このオプションを「放棄」することで、損失を免れることができます。一方、満期・６か月後に原資産Ａの株価が高騰して、時価２００万円になった場合は、このオプションを「行使」することで、差額分だけ利得が発生します。

 このように、オプションを適正に行使する（または放棄する）事で、原資産（金融資産など）の価格変動のリスクをヘッジすることができるのです。

 ある価値を有する原資産Ｓ(ｔ)を，満期Ｔの時点で権利行使価格Ｋ円（ストライク）で購入できるオプションを考えます。この時、Ｓ(Ｔ)がインデックスに相当します。

 満期Tの時点で原資産の価値が暴落し、時価がＫを下回れば、オプションを放棄することで損失を回避できます。

 一方、原資産の価値が高騰し、時価がＫを上回れば、権利を行使することで利得ｈ(Ｓ)＝Ｓ(Ｔ)－Ｋが発生するのです。この取引の結果生じる利得ｈ(Ｓ)のことをペイオフ関数と言います。


 オプション取引を行う際は、予めその権利を購入する必要があります。この権利のお値段、つまりオプションの価格（価値）のことを「プレミアム」と言います。

 オプション取引に伴う利得は青のグラフ（ペイオフ関数）で表されますが、実際には既にプレミアムを支払っている状態なので、実際の収支は青のグラフよりもプレミアム分だけ下にシフトした赤のグラフのようになります。

 プレミアムは、将来時点Ｔで見込める利得を、現在時点（契約時点）での価値に換算したものです。

 オプション取引では、原資産の価値が時間と共に変動しています。これに伴って、オプションの価値・プレミアムもまた、時間的に変動しています。その変動は原資産（危険資産）と同様に、確率微分方程式で表現されます。


 ここまで、安全資産・危険資産、そしてプレミアムの微分方程式やリスクの市場価格の式を導いてきました。これらの式を基にして、プレミアムに関する方程式を導くことが出来ます。

 このBlack-Scholesの偏微分方程式に変数変換を施して熱伝導方程式に変換し、オプション取引の条件を適用した上で、解の重ね合わせ（積分）を行うことで、次のようなプレミアムの公式を得ることが出来ます。

 これがBlack-Scholesの公式です。


 また、原資産Ｓ(ｔ)が指数関数で表され、その指数が正規分布に従うと仮定されることから、Ｓ(ｔ)は対数正規分布に従うと仮定されます。正規分布と対数正規分布の関係について、補足しておきます。

金融資産の組合せ・ポートフォリオ

 資産運用の際は、様々な金融資産を組み合わせて保有することが多いわけですが、この金融資産の組合せ（構成）を「ポートフォリオ」を言います。ここでは簡単のため、２種類の金融資産ＡとＢの場合を考えてみます。

 金融資産Ａはリターンがμ_A，リスクはσ_Aであり、金融資産Ｂはリターンがμ_B，リスクはσ_Bであるとします。この両者のバランスに応じて、ポートフォリオは変わります。いま、リスクσを横軸、リターンμを縦軸にとってグラフを描いています。

 金融資産Ａが100%のポートフォリオは（σ_A,μ_A）、金融資産Ｂが100%のポートフォリオは（σ_B,μ_B）となります。そして、この２点を端点とする曲線（線分）ＡＢが、２種類の金融資産ＡとＢを任意の割合で組み合わせたポートフォリオの集合です。

 ここで、左側に凸となる頂点に相当するポートフォリオは、最もリスク（標準偏差＝分散の平方根）が少ないことから、「最小分散ポートフォリオ」と呼ばれています。

 また、最小分散ポートフォリオよりも上側の部分を有効フロンティアと言います。同じリスクに対して、より大きなリターンを見込める（＝有効である）ということです。


 それでは、２種類の金融資産ＡとＢの最適なポートフォリオはどのようにして決まるのか、について考えてみます。新たに、リターンがｒ，リスクは０の無リスク資産を仮定します。リスクを取らなくても、既にｒのリターンが得られるという条件です。

 この無リスク資産（０,ｒ）から、有効フロンティアに向かって接線を引きます。この時の接点に相当するポートフォリオ（σ_M,μ_M）が最適な組合わせとされています。

 また、接線の傾きをリスクの市場価格λと言います。もともと、リスクを冒さずしてｒのリターンが得られるのに、敢えてσだけのリスクを冒すことで、μ－ｒだけリターンを上乗せすることが出来る、という意味です。冒すリスクに対して、どれだけの追加リターンが期待できるか、の指標です。

安全資産と危険資産の考え方

 現在時点における価値（元金）がS₀の試算を年利ｒで運用する場合、この資産のｔ年後の価値は、現在の価値に「e^rt」を乗じることで、S₀e^rtとなります。このような将来時点における価格のことを「フォワード価格」という事があります。

 また、将来時点（ｔ年後）の価値が判っている時に、これを現在の価値に換算する場合は、将来の価値に「e^-rt」を乗じることで計算することが出来ます。この乗数を「ディスカウント・ファクター」と言います。

 また、資産価値の関数Ｓ(ｔ)を微分すると、次のような微分方程式が得られます。

 ある時点（期間）での元金をＳとして、利率ｒの連続金利を適用した場合、期間Δｔの間に利子ΔＳが発生したとすると、「（利子）／（元金）＝（利率）×（期間）」の関係が成り立ちます。


 さて、定期預金のように、普通の複利法であれば、例えば１年毎のように「定期的に」利子が上乗せされます。これに対して、連続複利を用いると、利子は連続的に上乗せされるため、資産価値の時間変動は連続的なものとなります。

 このように、安定的に資産価値が上昇する金融資産を安全資産と言います。安全資産は記号Ｂ(ｔ)で表します。

 左が資産価値の時間変化のグラフで、右が利子の確率分布です。安全資産では利子は常に一定として扱うため、利子ｒの出現確率が１となります。

 一方、株価などのように、その資産価値が時々刻々と上下に激しく変動する金融資産（金融商品）もあります。

 このような資産を運用した場合、大きな利益を上げることも期待できる半面、元本割れを起こしてしまう危険性もはらんでいます。このような金融資産を危険資産と言います。

 危険資産を数理モデルで表現する際は、平均的な変動（トレンド）は安全資産に準じるものとして、さらに不規則に変動する成分（ノイズ）を考慮します。

 トレンドは安全資産に準ずるものとして、その利率をμと表すことにします。このμは平均的な利率（利益率）に相当し、「リターン」と言います。

 また、このノイズはブラウン運動に従うものとし、これをｚ(ｔ)とします。また、この振動の振幅をσとします。このσは利率（利益率）の変動の幅の大きさに相当し、「ボラティリティ」または「リスク」と言います。

連続複利の概念

 複利法とは、元金によって生じた利子を次期（次年）の元金に組み込んでいく方式です。例えば「元金をS₀,年利をr」の条件で預金すると、次のように預金額は増えて行きます。

 １年後には元金S₀に利子S₀r（＝利率×元金）が新たに組み込まれる形で、元利合計（預金額）が増えていきます。

 ２年後には元金S₁に利子S₁r（＝利率×元金）が新たに組み込まれる形で、元利合計（預金額）が増えていきます。

 つまり、１年後の預金額をS₁、２年後の預金額をS₂…ｔ年後の預金額をS_tとすると、この間預金の出し入れや、利率の見直しが発生しないものと仮定すると

（ｔ年後の預金額）＝（元金）×｛１＋（利率）｝^（年数）

のように表すことができます。

 上の例では１年ごとに利子が上乗せされる条件（１年複利）を想定しました。これがもし、半年ごとに利子を上乗せする場合（半年複利）は、１年を２期に分けるので、半年ごとに利率(ｒ/２)分ずつ、つまり、１年の間に２回、利子が上乗せされます。

 同様にして、１年をｎ期に分ける場合（１/ｎ年複利）は、１/ｎ年ごとに利率(ｒ/ｎ)分ずつ、つまり、１年の間にｎ回、利子が上乗せされます。この回数ｎを∞に持っていくと、連続的に利子が上乗せされることになります。つまり、連続的に預金が増加するということです。

 ネイピア数eを用いると、１年後の元利合計S₁は簡単に記述することができます。

 ここで、元金をS₀,年利をrの連続複利で運用する場合を考えてみます。この場合、次のようになるので

 このイメージをグラフで表してみます。

 通常の１年複利や半年複利の場合は、１年毎または半年毎に元利合計が増えて行くので、資産価値は階段状に上っていきます。この感覚を細かくしていくと、やがて、滑らかなカーブに近づいていきます。このカーブが連続複利に相当します。実際問題としては一定の時間間隔ごとに、段階的に預金が増加する（利子が上乗せされる）わけですが、理論的に解析する際は、連続的な関数の方が数学的にも扱いやすいので、連続金利を用います。

電力需要と気温の関係

　2008,2009,2010年度のデータを基に、東北６県および新潟県の電力需要と気温の関係を調べたものです。夏と冬の電力需要と平均気温の相関関係が良く分かります

　冬に比べて夏の感応度が大きいのも特徴的です。

　夏の間は冷房機器を稼働するために多くの電力を用います。一方、冬の暖房については、エアコンなどの暖房機器の他にも、石油ストーブなど電力に依存しない手段もあるので、夏に比べて感応度が鈍るのかも知れません。

夏の暑さと家計消費

　今回は「前年よりも夏の暑さが増すと、家計の消費支出は増えるのか？それとも減るのか？」について分析してみました。

　使用したデータは家計調査(家計収支編) 時系列データ(二人以上の世帯)を用いて、2005年～2015年における各年の第３四半期（７～９月）における「１世帯当たりの支出の対前年同期実質増減率（％）」と「気温の前年差（℃）」です。

　ここでは、家計消費の評価に際して、物価水準の変動の影響を除去した「実質」増減率を用いています。また、気温については、管区気象台および沖縄気象台の観測値（札幌，仙台，東京，大阪，福岡，沖縄）を基に、管区内人口に応じて重み付けした平均値（加重平均）を用いました。なお、気温は７～９月の月毎の前年差の平均値です。

　消費支出全体の傾向としては、前年よりも暑さが増すと、消費支出は増える傾向にあるようです。ざっくり言って、暑い夏は経済効果にはプラスに働くようです。

　やはり、喉が渇くので飲料の需要は増加傾向のようですね。

　
　そして、暑さが増すとその分、汗もかきやすいので・・・

　暑い夏は（日射しにも恵まれるので）サイクリングも楽しめる、ということ？

　夏の暑さが増すということは、やはり忘れてはいけないのがエネルギー需要です。冷房の需要は高まる一方、給湯の需要は伸び悩みます。

　暑い夏休みには余り勉強したくない・・・という気持ちは、何となくわかります。

　私は非喫煙者なのでわかりませんが、暑さが増すと、吸いたくなる・・・ものなのでしょうか？

　最後にもう一つ、夏の暑さと卵の消費は逆相関となるようです。なぜでしょう？

夏の気温とビールの売上の関係

　2004年～2015年の各7,8,9月（第３四半期）のビールの売上と気温の関係を調べてみました。

　ここで、ビールの売り上げは月別の売上を箱数に換算したものを用いています。１箱は大瓶（633ml）×20本で換算されています。また、気温は東京と大阪の月平均気温の算術平均を用いています。

　この結果、気温が上がるにつれて、売り上げも上がると言う「正の相関関係」が見られました。近似直線の傾きに相当する感応度を見てみると、約８７万箱／℃と言うことが判ります。

　仮に、大瓶１本の価格を「税抜で２９５円」とした場合、月平均気温１℃に対して、約５１億円のインパクトがある、という計算になります。

　ひと月当たりの売り上げを仮に１０００万箱とした場合、その金額は５９０億円規模となります。つまり、気温１℃でひと月の売上の１割近くが変動すると考えることができます。