前々回の記事では「連続体の運動方程式」を導出しました。続いて、前回の記事では「流体力学の方程式」を導出しました。そこで、今回は「弾性体における運動方程式」と導出し、さらに弾性体を伝わる波(弾性波)の支配方程式(波動方程式)を導いてみます。
まずは「弾性体の運動方程式」を導出します。今回使用するのは次の4つの式です。

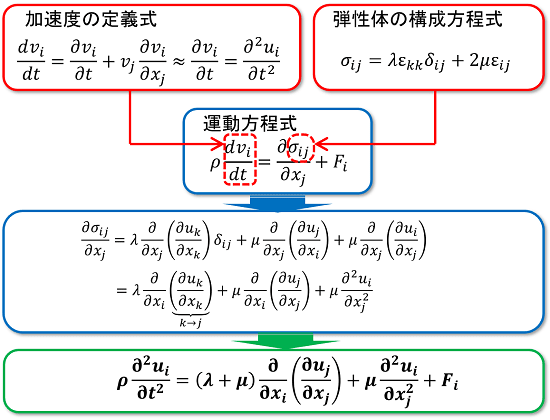
前回の記事と同様に、「加速度の定義式」と「弾性体の構成方程式(フックの法則=応力とひずみの関係式)」を「運動方程式」に代入します。
弾性体の場合は、変位勾配が小さいと考えられるため、加速度の式(ラグランジュ微分)の非線形項を無視できると考えます。つまり、加速度はそのまま「変位を時間で2階微分したもの」として扱います。
後は式を整理して「弾性体の運動方程式」の形が現れます(下図・緑枠)。もし、加速度が無ければ(静止状態であれば)、この式は「変位の平衡方程式」となります。
それでは、この方程式から弾性波の支配方程式(波動方程式)を導いてみます。今回は2種類のアプローチを行います。
まずは、次のようにxi軸方向の運動方程式(A)をxiで微分します。x‐y‐z系で言えば、x軸方向の方程式をxで微分するものです。同様に、y軸方向の方程式をyで、z軸方向の方程式をzでそれぞれ微分し、辺々足し合わせるものです。

さて、あるxi軸方向の変位をxiで微分したものは、xi軸方向の垂直ひずみεiiとなります。上図の式の中で「e=∂ui/xi=∂uj/xj」と集約したものは、x‐y‐z系で言えば、x、y、z各方向の垂直ひずみεxx、εyy、εzzの和に相当します。これを「体積ひずみ」と呼びます。
従って、ここで得られた波動方程式は「体積ひずみeが弾性体中を伝播する」ことを表します。それでは、この「体積ひずみ」について、次の図のような直方体状の微小片を例に考えてみましょう。
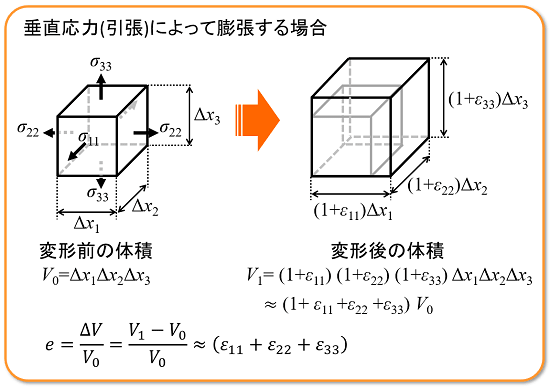
いま、この微小片の各面に垂直応力が作用した結果、各辺が伸びて体積が増加した状況を想定します。この場合は微小片の体積が膨張したことになります。このとき、体積ひずみeは「(体積変化)/(元の体積)」で表され、「3方向の垂直ひずみの和」にほぼ等しくなります。
弾性体内でこのような体積変化(膨張や圧縮)を生じ、それが波動として伝播して行きます。このような波は「圧力波(P波)」と呼ばれています。
続いて、xi軸方向の運動方程式(A)とxj軸方向の運動方程式(B)を考えます。方程式(B)をxiで微分、さらに方程式(A)をxjで微分し、辺々引き算します。
x‐y‐z系で例えると、x軸方向の方程式をyで微分、y軸方向の方程式をxで微分し、辺々引き算するようなものです。

今度はωkが伝播する波動方程式が得られました。このωkは「∂uj/xi-∂ui/xj」を集約したものです。この式の形は「どこかで見たことがある」ような気がします。
それもそのはず、ωkは変位ベクトル(u)の回転(rot u)のxk軸方向成分に相当します。また、微分の形を見ると「せん断ひずみεij」とよく似ています。
そこで、せん断ひずみ:ε12と、変位ベクトルの回転の成分:ω3を比較してみましょう。
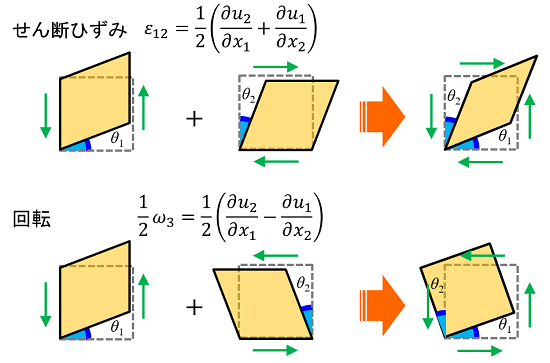
上の図は左から順に「(第1項の変形)+(第2項の変形)→(両者を合わせた変形)」を表しています。
ここで、「ε12」と「ω3」は共に第1項は等しいので、変形も等しくなります。一方、第2項は正負の向きが逆なので、その変形も互いに逆向きとなります。この結果、両者を合わせた変形も異なってきます。せん断ひずみ(ε12)の変形は「斜めに潰れる(ひしゃげる)」ように変形します。一方、回転(ω3)の変形は「クルリと回転する」ように変形します。
つまり、弾性体内では部分的に回転するような変形を生じ、それが波動として伝播して行くことが示されました。このような波は「せん断波(S波)」と呼ばれています。
まずは「弾性体の運動方程式」を導出します。今回使用するのは次の4つの式です。

前回の記事と同様に、「加速度の定義式」と「弾性体の構成方程式(フックの法則=応力とひずみの関係式)」を「運動方程式」に代入します。
弾性体の場合は、変位勾配が小さいと考えられるため、加速度の式(ラグランジュ微分)の非線形項を無視できると考えます。つまり、加速度はそのまま「変位を時間で2階微分したもの」として扱います。
後は式を整理して「弾性体の運動方程式」の形が現れます(下図・緑枠)。もし、加速度が無ければ(静止状態であれば)、この式は「変位の平衡方程式」となります。

それでは、この方程式から弾性波の支配方程式(波動方程式)を導いてみます。今回は2種類のアプローチを行います。
まずは、次のようにxi軸方向の運動方程式(A)をxiで微分します。x‐y‐z系で言えば、x軸方向の方程式をxで微分するものです。同様に、y軸方向の方程式をyで、z軸方向の方程式をzでそれぞれ微分し、辺々足し合わせるものです。

さて、あるxi軸方向の変位をxiで微分したものは、xi軸方向の垂直ひずみεiiとなります。上図の式の中で「e=∂ui/xi=∂uj/xj」と集約したものは、x‐y‐z系で言えば、x、y、z各方向の垂直ひずみεxx、εyy、εzzの和に相当します。これを「体積ひずみ」と呼びます。
従って、ここで得られた波動方程式は「体積ひずみeが弾性体中を伝播する」ことを表します。それでは、この「体積ひずみ」について、次の図のような直方体状の微小片を例に考えてみましょう。

いま、この微小片の各面に垂直応力が作用した結果、各辺が伸びて体積が増加した状況を想定します。この場合は微小片の体積が膨張したことになります。このとき、体積ひずみeは「(体積変化)/(元の体積)」で表され、「3方向の垂直ひずみの和」にほぼ等しくなります。
弾性体内でこのような体積変化(膨張や圧縮)を生じ、それが波動として伝播して行きます。このような波は「圧力波(P波)」と呼ばれています。
続いて、xi軸方向の運動方程式(A)とxj軸方向の運動方程式(B)を考えます。方程式(B)をxiで微分、さらに方程式(A)をxjで微分し、辺々引き算します。
x‐y‐z系で例えると、x軸方向の方程式をyで微分、y軸方向の方程式をxで微分し、辺々引き算するようなものです。

今度はωkが伝播する波動方程式が得られました。このωkは「∂uj/xi-∂ui/xj」を集約したものです。この式の形は「どこかで見たことがある」ような気がします。
それもそのはず、ωkは変位ベクトル(u)の回転(rot u)のxk軸方向成分に相当します。また、微分の形を見ると「せん断ひずみεij」とよく似ています。
そこで、せん断ひずみ:ε12と、変位ベクトルの回転の成分:ω3を比較してみましょう。

上の図は左から順に「(第1項の変形)+(第2項の変形)→(両者を合わせた変形)」を表しています。
ここで、「ε12」と「ω3」は共に第1項は等しいので、変形も等しくなります。一方、第2項は正負の向きが逆なので、その変形も互いに逆向きとなります。この結果、両者を合わせた変形も異なってきます。せん断ひずみ(ε12)の変形は「斜めに潰れる(ひしゃげる)」ように変形します。一方、回転(ω3)の変形は「クルリと回転する」ように変形します。
つまり、弾性体内では部分的に回転するような変形を生じ、それが波動として伝播して行くことが示されました。このような波は「せん断波(S波)」と呼ばれています。

















