
きょうは、「四月バカの日」。この日に した
した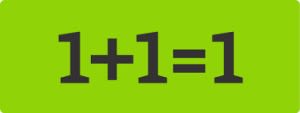 と「空飛ぶペンギン」に匹敵する話題が次。
と「空飛ぶペンギン」に匹敵する話題が次。
算数の答は、一通りのハズなのに、二通りの答があるという そんなバカな
そんなバカな

一見すると簡単な計算のように思える問題が、数学者も巻き込んだ論争になった。
iinaなら( )を優先して右側から計算する。
12÷2×3=12÷6=2
ところが、12÷2を優先して左側から計算すると
6×(1+2)=6×3=18
答が 「2」と「18」の2つに別れてしまった (・・?
日本では 12÷2(1+2)= という式を書いたら「意味不明」または「出題ミス」となる。小学生までは必ず「×」の表示が必要。
12÷2(1+2) は 12÷{2✖(1+2)} のつもりだった?
12÷2(1+2) は {12÷2}✖(1+2) のつもりだった?
もはや、この式を作った人にしか分らない。もし、問題作成者が「そこまで考えてなかった」のであれば、出題ミスということになる。
この3月にスマホのGoogleニュースにはさまれた情報でした。
ネット上の論争に発展した論点は、地域によって計算の順序の教え方が違うからというもの。
計算の順序の覚え方として、「PEMDAS」と「BOMDAS」というふたつの教え方があるのだそうだ。
アメリカをはじめとする地域では、計算順序をPEMDASと教える。つまりカッコ(Parenthesis)、指数(Exponent)、掛算(Multiplication)、割算(Division)、足算(Addition)、引算(Subtraction)という順序で計算するよう教える。
もうひとつ、イギリスではBODMASという覚え方がある。そして、こちらでは、カッコ(Bracket)、累乗(Order)、割算(Division)、掛算(Multiplication)、足算(Addition)、引算(Subtraction)の順序で計算すると教える。
きちんと答えが定まると思われる算数・数学でも、答えが決まらないということが起こる。
どのような考え方が前提になっているかを明確にした上で、議論をしなければなりません。
イギリス式だアメリカ式だと、計算のルールを増やしていけば、地域差が生じる。
従って、他人に式を見せる前に「誰が見ても出題者が考えた計算の順序を解釈して貰える」式にまとめておく必要があることに落着く。


 した
した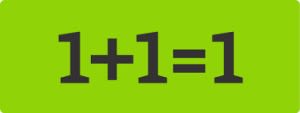 と「空飛ぶペンギン」に匹敵する話題が次。
と「空飛ぶペンギン」に匹敵する話題が次。算数の答は、一通りのハズなのに、二通りの答があるという
 そんなバカな
そんなバカな

一見すると簡単な計算のように思える問題が、数学者も巻き込んだ論争になった。
iinaなら( )を優先して右側から計算する。
12÷2×3=12÷6=2
ところが、12÷2を優先して左側から計算すると
6×(1+2)=6×3=18
答が 「2」と「18」の2つに別れてしまった (・・?
日本では 12÷2(1+2)= という式を書いたら「意味不明」または「出題ミス」となる。小学生までは必ず「×」の表示が必要。
12÷2(1+2) は 12÷{2✖(1+2)} のつもりだった?
12÷2(1+2) は {12÷2}✖(1+2) のつもりだった?
もはや、この式を作った人にしか分らない。もし、問題作成者が「そこまで考えてなかった」のであれば、出題ミスということになる。
この3月にスマホのGoogleニュースにはさまれた情報でした。
ネット上の論争に発展した論点は、地域によって計算の順序の教え方が違うからというもの。
計算の順序の覚え方として、「PEMDAS」と「BOMDAS」というふたつの教え方があるのだそうだ。
アメリカをはじめとする地域では、計算順序をPEMDASと教える。つまりカッコ(Parenthesis)、指数(Exponent)、掛算(Multiplication)、割算(Division)、足算(Addition)、引算(Subtraction)という順序で計算するよう教える。
もうひとつ、イギリスではBODMASという覚え方がある。そして、こちらでは、カッコ(Bracket)、累乗(Order)、割算(Division)、掛算(Multiplication)、足算(Addition)、引算(Subtraction)の順序で計算すると教える。
きちんと答えが定まると思われる算数・数学でも、答えが決まらないということが起こる。
どのような考え方が前提になっているかを明確にした上で、議論をしなければなりません。
イギリス式だアメリカ式だと、計算のルールを増やしていけば、地域差が生じる。
従って、他人に式を見せる前に「誰が見ても出題者が考えた計算の順序を解釈して貰える」式にまとめておく必要があることに落着く。

















その「加減乗除」とは、「足算(加法)」「引算(減法)」「掛算(乗法)」「割算(除法)」のことで、これを【四則演算(しそくえんざん)】という。
四則演算を行う時のポイントは、計算の優先順位は「カッコの中 → 掛算・割算 → 足算・引算」。
ということは、12÷2×3=12÷6=2 を導く。
でも子供の頃、学校ではiina様と同じように( )を優先して解いたように記憶しています。
解き方で回答が違ってくると困りますね。
>桜と、ほぼ同じに咲くのですね。
桃の節句の関係で、桃は3月の上旬~中旬に咲いていたように思いますが、近年はサクラの開花と同時期になってきました。
明治19年度から4月になったのであれば、iinaたちは「4月始まり」を当然のことと思う道理です。
> 子供の頃、学校では・・・( )を優先して解いたように記憶しています。
小学生のころに( )を使ったかどうかまでは記憶していませんが、教える順番があるのですね。まして、お国が違うと答えまで異なってしまうなんて・・・。
そんなバカなと思って、この話題を4月1日に
そんなバカな😅❓
まさかの「そんなバカな」算術でした。
まさに、そのとおりです。
踊る阿呆に見るアホウ。
どちら側に立ってもバカでいられます。
https://blog.goo.ne.jp/iinna/e/2de8ecfc65ddf4e6052528de40e20ccb