理科先生から頂いた計算式です。要は円の中に三角形を書いて、その斜辺を
求め、その三角形を更に分割していくと、だんだん円周に近づいていきます。
というもの。
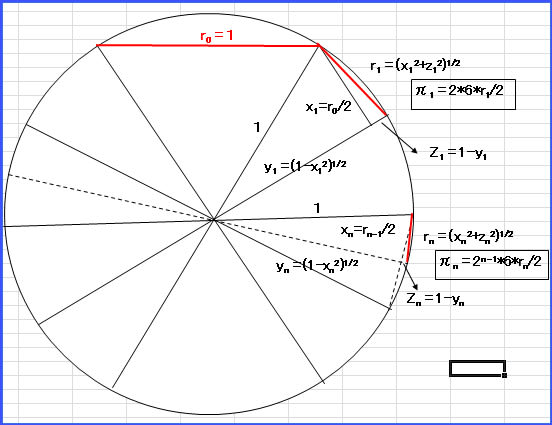
昔の人は一生を掛けて、これを計算していたんですよね。スゴイな~。
で、エクセルの計算式で再現したのが下記のものです。
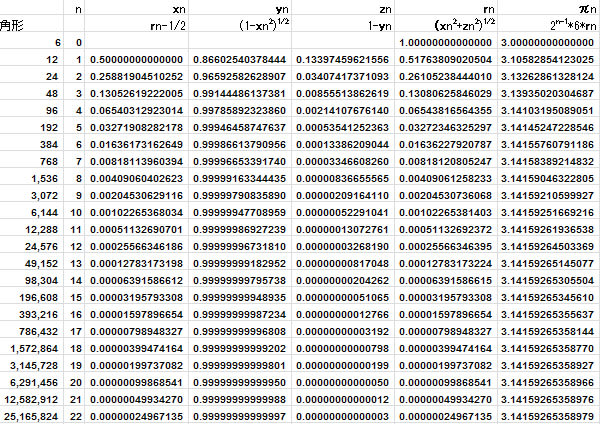
最初は6角形で「3」だったπが2516万角形!で「3.14」に
なっていくのが目に見えて面白いですよね♪
で、理科先生から「エクセルで計算すると15桁が限界みたい。」と
言われました。
で、気になって検索してみたら、こんな記事がありました。
日経PC21 / 演算誤差の正体 - IEEE 754 浮動小数点数の仕組み
http://pc.nikkeibp.co.jp/pc21/special/gosa/eg4.shtml
私の頭の理解では「箱がの中に入る数字の限界があり、それで表記
計算しているので誤差が出てしまう。」ということでしょうか?
たぶん、日常生活ではほとんど影響がないでしょう。だって下15桁
の計算は使わないでしょう?衛星軌道計算とか精密計算が必要な分野
では大変なことなんでしょうね。
ということで、久しぶりに『数学美』を見て楽しくなった19なの
でした。ではでは~。
PS.
計算つながりで調べた、ひとネタありましたので。
i-Podの電卓、通常は四則演算のみですが、

横にすると、、、

一昔前の関数電卓のような画面が♪
求め、その三角形を更に分割していくと、だんだん円周に近づいていきます。
というもの。


昔の人は一生を掛けて、これを計算していたんですよね。スゴイな~。

で、エクセルの計算式で再現したのが下記のものです。


最初は6角形で「3」だったπが2516万角形!で「3.14」に
なっていくのが目に見えて面白いですよね♪

で、理科先生から「エクセルで計算すると15桁が限界みたい。」と
言われました。

で、気になって検索してみたら、こんな記事がありました。
日経PC21 / 演算誤差の正体 - IEEE 754 浮動小数点数の仕組み
http://pc.nikkeibp.co.jp/pc21/special/gosa/eg4.shtml
私の頭の理解では「箱がの中に入る数字の限界があり、それで表記
計算しているので誤差が出てしまう。」ということでしょうか?

たぶん、日常生活ではほとんど影響がないでしょう。だって下15桁
の計算は使わないでしょう?衛星軌道計算とか精密計算が必要な分野
では大変なことなんでしょうね。

ということで、久しぶりに『数学美』を見て楽しくなった19なの
でした。ではでは~。

PS.
計算つながりで調べた、ひとネタありましたので。
i-Podの電卓、通常は四則演算のみですが、

横にすると、、、

一昔前の関数電卓のような画面が♪















