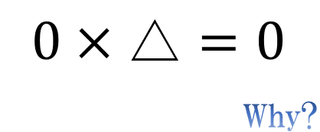
0はなぜ何をかけても0になるのか ❔
無いことを表す数「0」。0という概念を数として認めたことで、数学は飛躍的な進歩を遂げました。
ゼロは、数の中でも非常に特殊な性質をもっています。
それは0のかけ算。つまり「何に0をかけても0になり、0に何をかけても0になる」ことです。
△ × 0 = 0
0 × △ = 0
しかし、「無い」数のかけ算とは不可解なものです。無いものをどうやってかけるのか ❔
そこで、0のかけ算のイメージとその利便性について綴ってまいります。
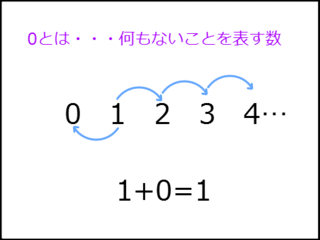
0は、何もないことを表す数であり、1の直前の整数です。
「1に0を足す」ことは、「1に何もないを足す」⇒「1に何も足さない」ことを意味します。
何も足さないのですから、1は1のまま。
そのため、1+0=1 となります。
0のかけ算は一体何を意味しているのでしょうか。「何もない」をかける、では意味がよく分かりません。

そこで「2×3=6」「2×0=0」「0×3=0」の3つの視点から具体的にイメージしてみます。
まず、右のように
「机の上には水が2ℓ入ったビンが3本あります。このとき、机の上に水は全部で何リットルあるでしょうか❔」
これが、2×3=6です。
 「水が2ℓ入ったビンが0本あります(=1本もありません)。
「水が2ℓ入ったビンが0本あります(=1本もありません)。
このとき、水は全部で何リットルあるでしょうか?」
これが、2×0=0です。
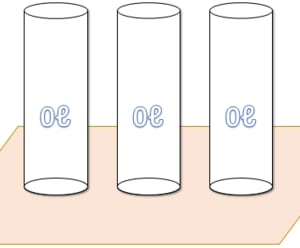 では、
では、
「空ビン(=水が0ℓ)が3本あります。このとき、水は全部で何リットルあるでしょうか?」
これが、0×3=0です。
水が0ℓ入ったビンが机の上にどれだけあろうと、机の上にある水は0ℓから変わりません。
これが「0に何をかけても0になる」理由です。
上の3つの例を見比べると、0のかけ算のイメージがついたのではないでしょうか。
0のかけ算の存在は、「0×2 + 1×1 + 2×0 + 3×2 = ❔ 」のようにかけ算と足し算が組み合わさったときに便利になってきます。
身近な例だと、商品の集計がこれに当たります。
たとえば「水〇ℓ入りのビンがそれぞれ何本あるか」から、「ビンが合計何本あって、水が合計何ℓあるか」を集計したい場合。

商品の数は、毎日変動します。
今日はたまたま2ℓ入りのビンがなかったですが、明日の仕入れで入ってくるかもしれません。また、今ある3ℓ入りのビンは明日にはないかもしれません。
ここで、いちいち「今日は2ℓ入りのビンがないから、1×1+3×2=7ℓだな。で、ビンの数を計算するときは0ℓのビンも集計するから…」と判断するのは非効率です。
商品の種類が少ないならまだ良いですが、商品の種類が100種を超えてくると非常に面倒になってきますよね。

そんなときに役に立つのが0のかけ算です。
0のかけ算を利用すると、Excelで右のような表を作ることができます。
D列に各商品の数量を入力するだけで、0本だろうと0ℓビンだろうと関係なく計算し「ビンが合計何本あって、水が合計何ℓあるか」を算出できるようになるのです。
今回の例だと、黄色いセルの数字が5なので、ビンは合計5本。
緑のセルの数字が7なので、水は合計7ℓとなります。
商品の種類が増えれば増えるほど、0のかけ算の存在による計算の利便性は高まっていきます。
物が大量に増えた現代において、0のかけ算の存在は私たちの生活に欠かせないものとなっているのです。
まとめ
① 0は何もないことを表す数であり、1の直前の整数である。
② 水が2ℓ入ったビンが机の上から無くなると、机の上にある水も0ℓになる。これが0をかけると0になる理由。
③ 水が0ℓ入ったビンが机の上にどれだけあろうと、机の上にある水は0ℓ。これが0に何をかけても0になる理由。
④ 0のかけ算が本領を発揮するのは、かけ算と足し算が組み合わさったとき。身近な例だと商品を集計するときに便利。

無いことを表す数「0」。0という概念を数として認めたことで、数学は飛躍的な進歩を遂げました。
ゼロは、数の中でも非常に特殊な性質をもっています。
それは0のかけ算。つまり「何に0をかけても0になり、0に何をかけても0になる」ことです。
△ × 0 = 0
0 × △ = 0
しかし、「無い」数のかけ算とは不可解なものです。無いものをどうやってかけるのか ❔
そこで、0のかけ算のイメージとその利便性について綴ってまいります。
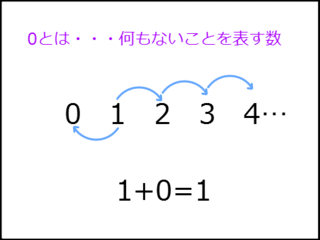
0は、何もないことを表す数であり、1の直前の整数です。
「1に0を足す」ことは、「1に何もないを足す」⇒「1に何も足さない」ことを意味します。
何も足さないのですから、1は1のまま。
そのため、1+0=1 となります。
0のかけ算は一体何を意味しているのでしょうか。「何もない」をかける、では意味がよく分かりません。

そこで「2×3=6」「2×0=0」「0×3=0」の3つの視点から具体的にイメージしてみます。
まず、右のように
「机の上には水が2ℓ入ったビンが3本あります。このとき、机の上に水は全部で何リットルあるでしょうか❔」
これが、2×3=6です。
 「水が2ℓ入ったビンが0本あります(=1本もありません)。
「水が2ℓ入ったビンが0本あります(=1本もありません)。このとき、水は全部で何リットルあるでしょうか?」
これが、2×0=0です。
 では、
では、「空ビン(=水が0ℓ)が3本あります。このとき、水は全部で何リットルあるでしょうか?」
これが、0×3=0です。
水が0ℓ入ったビンが机の上にどれだけあろうと、机の上にある水は0ℓから変わりません。
これが「0に何をかけても0になる」理由です。
上の3つの例を見比べると、0のかけ算のイメージがついたのではないでしょうか。
0のかけ算の存在は、「0×2 + 1×1 + 2×0 + 3×2 = ❔ 」のようにかけ算と足し算が組み合わさったときに便利になってきます。
身近な例だと、商品の集計がこれに当たります。
たとえば「水〇ℓ入りのビンがそれぞれ何本あるか」から、「ビンが合計何本あって、水が合計何ℓあるか」を集計したい場合。

商品の数は、毎日変動します。
今日はたまたま2ℓ入りのビンがなかったですが、明日の仕入れで入ってくるかもしれません。また、今ある3ℓ入りのビンは明日にはないかもしれません。
ここで、いちいち「今日は2ℓ入りのビンがないから、1×1+3×2=7ℓだな。で、ビンの数を計算するときは0ℓのビンも集計するから…」と判断するのは非効率です。
商品の種類が少ないならまだ良いですが、商品の種類が100種を超えてくると非常に面倒になってきますよね。

そんなときに役に立つのが0のかけ算です。
0のかけ算を利用すると、Excelで右のような表を作ることができます。
D列に各商品の数量を入力するだけで、0本だろうと0ℓビンだろうと関係なく計算し「ビンが合計何本あって、水が合計何ℓあるか」を算出できるようになるのです。
今回の例だと、黄色いセルの数字が5なので、ビンは合計5本。
緑のセルの数字が7なので、水は合計7ℓとなります。
商品の種類が増えれば増えるほど、0のかけ算の存在による計算の利便性は高まっていきます。
物が大量に増えた現代において、0のかけ算の存在は私たちの生活に欠かせないものとなっているのです。
まとめ
① 0は何もないことを表す数であり、1の直前の整数である。
② 水が2ℓ入ったビンが机の上から無くなると、机の上にある水も0ℓになる。これが0をかけると0になる理由。
③ 水が0ℓ入ったビンが机の上にどれだけあろうと、机の上にある水は0ℓ。これが0に何をかけても0になる理由。
④ 0のかけ算が本領を発揮するのは、かけ算と足し算が組み合わさったとき。身近な例だと商品を集計するときに便利。


















7月21日笑撃画像・夕景の画像が楽しいです。
またの掲載を楽しみにしております。
https://blog.goo.ne.jp/iinna/e/ce04ed9c9ac94b6fb62faa07396f4239
一方のいわどの山荘主人さんブログは、”浦和よさこい” 見物でした。 そんな季節ですね。
iinaも近くの街で ”よさこい” を見物しました。
さいきんは、阿波踊りのように”よさこい”も全国的になりました。
むかしに、表参道でも流してましたが、浅草の三社祭に重なっていたためか、iinaとしては行けなかったです。
そんな思いでいましたから、昨年に偶然ながら ”よさこい” をようやく見れて嬉しかったです。
アップで踊り手の表情を切り撮っていて、そうとう数を
https://blog.goo.ne.jp/iinna/e/45975e7027e44ebc7f7f7c9f1f6e78bf
安心の「掛け」算でした。
分かりやすい解釈をしていただき嬉しiina~
それに、 △ × 0 = 0 と 0 × △ = 0 は、意味合いが違うちょんやけね。
そこんとこをうまいこと解説したとね。
ここに来るんが遅れてゴメン。
(^π^)/~~~バイバイ
「ゼロで割ってはいけない理由」は 次でしたね。^^
https://blog.goo.ne.jp/iinna/e/744887d74fedec802604beecd7e3bcde