微分は「微かに分かる」。積分は「分かった積もり」。
・・・ つまり、微かに分かっただけなのに、分かった積もりになる分野。
分かっていないのに分かった積もりになっている人が意外と多いということを・・・。
分かった積もりの怖いところは思い込みが入り込んでしまうこと。思い込みが入ると、再確認を怠りがちになる。
分かった積もりになって暴走してしまうのが悲劇の始まり。
分かった積もりよりも微(かす)かに分かる方がリスクが少なくて済む。
微かに分かったら、調べるなり、質問するなりして、正しく分かるようにする。
地味ながらこの繰り返しが成果につながる道ではないかと考える。
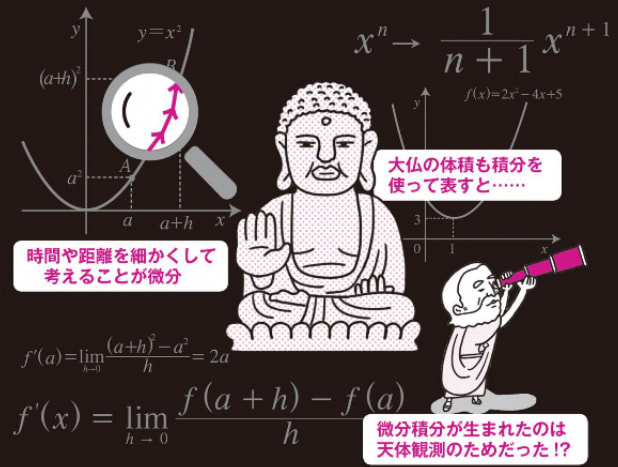
微分と積分の概念を具体的に捉える時には、速度と距離の関係を例に捉えるとよい。
距離を(時間で)微分すると速度を求めることができる。
速度を(時間で)積分すると距離を求めることができる。
これからわかるように、微分と積分はそれぞれ逆の操作になっている。

・・・ つまり、微かに分かっただけなのに、分かった積もりになる分野。
分かっていないのに分かった積もりになっている人が意外と多いということを・・・。
分かった積もりの怖いところは思い込みが入り込んでしまうこと。思い込みが入ると、再確認を怠りがちになる。
分かった積もりになって暴走してしまうのが悲劇の始まり。
分かった積もりよりも微(かす)かに分かる方がリスクが少なくて済む。
微かに分かったら、調べるなり、質問するなりして、正しく分かるようにする。
地味ながらこの繰り返しが成果につながる道ではないかと考える。
微分と積分の概念を具体的に捉える時には、速度と距離の関係を例に捉えるとよい。
距離を(時間で)微分すると速度を求めることができる。
速度を(時間で)積分すると距離を求めることができる。
これからわかるように、微分と積分はそれぞれ逆の操作になっている。
| 微分とは | 積分とは | ||
| 10分おきに車が、 次の距離を進んだとすると、 5Km, 5Km, 10Km, 15Km, 15Km, 10Km 計60Km | それぞれの区間の平均時速は、 次のように計算される 30Km/h, 30Km/h, 60Km/h, 90Km/h, 90Km/h, 60Km/h (km/hは時速を表す単位) | 10分おきに、 次の平均速度で進むとすると 30Km/h, 30Km/h, 60Km/h, 90Km/h, 90Km/h, 60Km/h | 次の距離を進んだことになる 5Km, 5Km, 10Km, 15Km, 15Km, 10Km 計60Km |

















「微かに分かる」のが微分。
「分かった積もり」になるのが積分。
などと身勝手にブログにしてしまいました。
GWからTを取ったCWが、ことしの10日間ほどです。
ゴールデンウィーク コロナウィーク
あいにくと、物理学者はからみませんが「数学者と統計学者と会計士」のジョークがあります。
https://blog.goo.ne.jp/iinna/e/bf6d943131349e2dcc03e6d54ff5e4af
つぎには、数学者に哲学者と科学者が額面をそろえると、こうなります・・・
https://blog.goo.ne.jp/iinna/e/5666f617715205ce1adb31f2fba49d36
では、こんな「数」の話題をコロナの気休めにいかがでしょうか("^ω^)・・・
https://blog.goo.ne.jp/iinna/e/39b642eb7d9464322e233a8cd4d46054
失礼いたしました。
* kei_matsuuraさんの当該ブログ記事のアドレスをコメント上(iina)に置いています。
すばらしい解釈たい。
多分、他聞をはばからずに多文をもちいずに一行にまとめた名言と思うばい。
バイバイ(^π^)/~~~
微分「びぶん」から「たぶん」を多用した文章を考えたとおもいます。
ひさしぶりな「数」の話題に、 (^π^) さんからコメントをいただき、嬉しiina~
また、オコシください。