アメダス観測値を基に、新潟県内の昨シーズンの積算降雪量の分布を解析してみます。
さて、アメダスは不規則に点在しています。点在している数値データを基に面的な分布をどのようにして求めれば良いでしょうか。ここで、有限要素法のアイデアが浮かびました。有限要素法では領域を三角形要素に分割していました。そこで、今回は近隣の3つの観測点を頂点とする三角形要素を作ってみます。
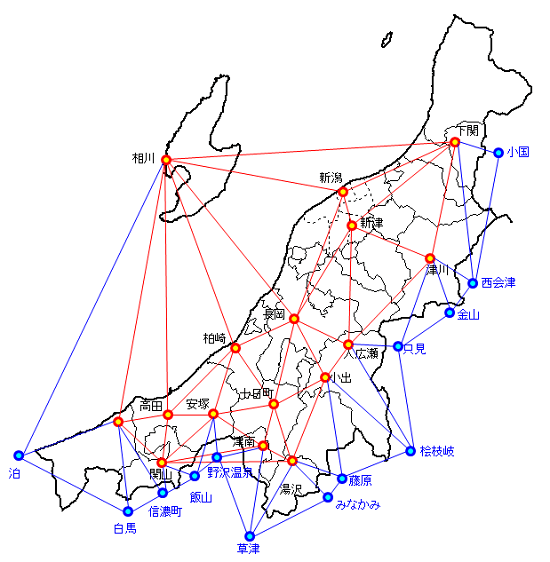
続いて、その三角形要素の中で線形補間する事を思いつきました。3つの頂点をO、A、Bとし、OAとOBのベクトルからなる△OAB上の任意の点はベクトル方程式OP=sOA+tOB(sとtは媒介変数)で表される事を利用します。

この状態では線形補間なので、さらにこれを曲面的に滑らか分布に補正する処理を施して、次のような分布を得ました。尚、一部地域は解析の対象外としてグレー表示しております。

(さらに、詳細な観測データを加えると、より細かい特性が見えてくる・・・)
さて、アメダスは不規則に点在しています。点在している数値データを基に面的な分布をどのようにして求めれば良いでしょうか。ここで、有限要素法のアイデアが浮かびました。有限要素法では領域を三角形要素に分割していました。そこで、今回は近隣の3つの観測点を頂点とする三角形要素を作ってみます。

続いて、その三角形要素の中で線形補間する事を思いつきました。3つの頂点をO、A、Bとし、OAとOBのベクトルからなる△OAB上の任意の点はベクトル方程式OP=sOA+tOB(sとtは媒介変数)で表される事を利用します。

この状態では線形補間なので、さらにこれを曲面的に滑らか分布に補正する処理を施して、次のような分布を得ました。尚、一部地域は解析の対象外としてグレー表示しております。

(昨シーズンの新潟県内の積算降雪量 ※グレー域は解析対象外とした)
(さらに、詳細な観測データを加えると、より細かい特性が見えてくる・・・)

















