次の図のようなベクトル場を考えてみます。

この流れ場(ベクトル場)の中に、羽根車を置いた場合にどうなるでしょうか・・・。
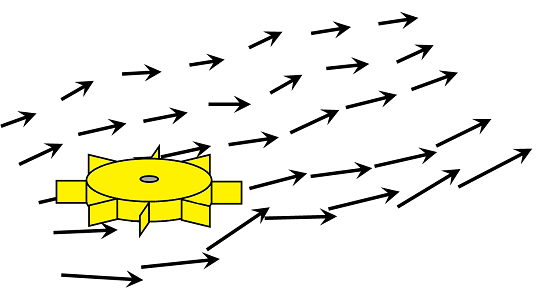
流れ場(ベクトル場)の流れの中で、羽根車はクルクルと回りながら下流へと流されて行きます。
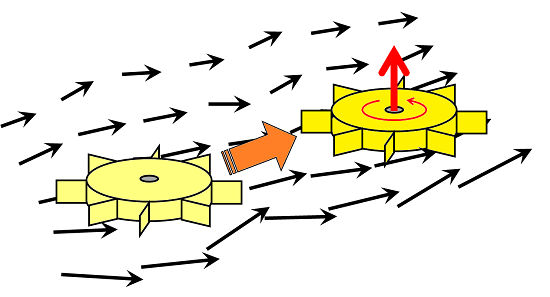
この時、羽根車を回転させようとする効果を表すパラメータが「渦度」です。渦度は、回転軸上の向きを持つ「ベクトル量」として表されます。

今度は、この羽根車を台の上に乗せ場合について考えてみます。

この台に向かって横から流れを与えると(ベクトル場を与えると)、この台はゆっくりと回転を始めます。これに伴って、渦度ベクトルを生じます。

台の上に羽根車を乗せた場合、台と羽根車は一体となって回転するため、両者の持つ渦度ベクトルは共通のものとなります。しかし、これは「台の外から見た場合」の話です。

羽根車と一緒に「台の上に乗った状態」で、この羽根車を見ると・・・羽根車は止まっているように見えます。つまり、羽根車の持つ渦度(ベクトル)はゼロという事になります。

回転している台の上で、羽根車にはさらに別の流れを横から加えてみます。これに伴い、羽根車には新たな渦度ベクトルが加わることになります。羽根車には、台の回転に伴う渦度ベクトル(青)と新たに加わった渦度ベクトル(赤)が合わさった渦度ベクトルが働きます。ただし、これは「台の外から見た場合」の話です。

一方、羽根車と一緒に「台の上に乗った状態」から見てみると、羽根車に加わる渦度ベクトルは次の図のように認識されます。

以上のように、回転台から一歩離れた所から見た場合と、羽根車と一緒に台に乗った場合とでは、「羽根車に働いている」と認識される渦度ベクトルの大きさは異なります。
ここで、回転台から一歩離れた所から見た場合の渦度(青+赤)を「絶対渦度」、羽根車と一緒に台に乗った場合に認識できる渦度(赤)を「相対渦度」と言います。
この「絶対渦度」と「相対渦度」の概念は、地球を取り巻く大気の流れに伴って生じる渦度を考える際に重要になります。「地球上にいる人」が「地球上で生じる渦度」を見た場合は「相対渦度」となる一方、「宇宙空間のある地点に固定された場所」から「地球上で生じる渦度」を見た場合は「絶対渦度」という事です。

地球は自転しているので、地球上で運動する物体・流体は既に自転に伴う渦度ベクトルを持っています。この大きさは、地軸上にある極が最大となり、極から赤道に近づくにつれて小さくなります。
これは、(各地点における)自転に伴う渦度ベクトルは、地表面に対して垂直に働くためです。北半球の場合、北極における渦度ベクトルを分解して、地面に垂直な成分が作用すると考えます。この大きさがコリオリ・パラメーター(f=2Ωsinφ、Ω:自転の角速度、φ:緯度)です。
このように、自転に伴う渦度の大きさ(コリオリ・パラメーター)が、緯度によって変わる効果を「ベータ効果」と言います。

この流れ場(ベクトル場)の中に、羽根車を置いた場合にどうなるでしょうか・・・。

流れ場(ベクトル場)の流れの中で、羽根車はクルクルと回りながら下流へと流されて行きます。

この時、羽根車を回転させようとする効果を表すパラメータが「渦度」です。渦度は、回転軸上の向きを持つ「ベクトル量」として表されます。

今度は、この羽根車を台の上に乗せ場合について考えてみます。

この台に向かって横から流れを与えると(ベクトル場を与えると)、この台はゆっくりと回転を始めます。これに伴って、渦度ベクトルを生じます。

台の上に羽根車を乗せた場合、台と羽根車は一体となって回転するため、両者の持つ渦度ベクトルは共通のものとなります。しかし、これは「台の外から見た場合」の話です。

羽根車と一緒に「台の上に乗った状態」で、この羽根車を見ると・・・羽根車は止まっているように見えます。つまり、羽根車の持つ渦度(ベクトル)はゼロという事になります。

回転している台の上で、羽根車にはさらに別の流れを横から加えてみます。これに伴い、羽根車には新たな渦度ベクトルが加わることになります。羽根車には、台の回転に伴う渦度ベクトル(青)と新たに加わった渦度ベクトル(赤)が合わさった渦度ベクトルが働きます。ただし、これは「台の外から見た場合」の話です。

一方、羽根車と一緒に「台の上に乗った状態」から見てみると、羽根車に加わる渦度ベクトルは次の図のように認識されます。

以上のように、回転台から一歩離れた所から見た場合と、羽根車と一緒に台に乗った場合とでは、「羽根車に働いている」と認識される渦度ベクトルの大きさは異なります。
ここで、回転台から一歩離れた所から見た場合の渦度(青+赤)を「絶対渦度」、羽根車と一緒に台に乗った場合に認識できる渦度(赤)を「相対渦度」と言います。
この「絶対渦度」と「相対渦度」の概念は、地球を取り巻く大気の流れに伴って生じる渦度を考える際に重要になります。「地球上にいる人」が「地球上で生じる渦度」を見た場合は「相対渦度」となる一方、「宇宙空間のある地点に固定された場所」から「地球上で生じる渦度」を見た場合は「絶対渦度」という事です。

地球は自転しているので、地球上で運動する物体・流体は既に自転に伴う渦度ベクトルを持っています。この大きさは、地軸上にある極が最大となり、極から赤道に近づくにつれて小さくなります。
これは、(各地点における)自転に伴う渦度ベクトルは、地表面に対して垂直に働くためです。北半球の場合、北極における渦度ベクトルを分解して、地面に垂直な成分が作用すると考えます。この大きさがコリオリ・パラメーター(f=2Ωsinφ、Ω:自転の角速度、φ:緯度)です。
このように、自転に伴う渦度の大きさ(コリオリ・パラメーター)が、緯度によって変わる効果を「ベータ効果」と言います。

















