大気の流れを表す指標には「速度ポテンシャルΦ」と「流れ関数(流線関数)Ψ」があります。
大気は速度ポテンシャルΦの低い方から高い方に流れ、その極大・極小は収束・発散の中心を表します。また、流れの速度ベクトルの向きは、速度ポテンシャルの等値線(Φ=一定)に対して直角です。簡単な場を考えてみましょう。
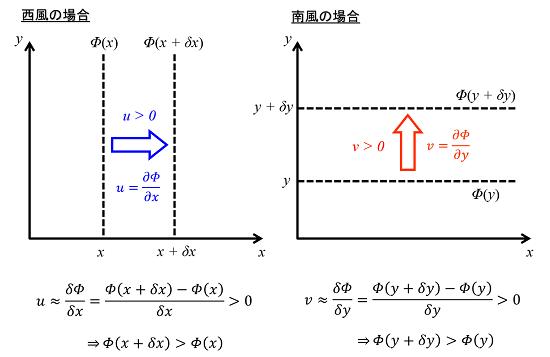
一様な西風と南風の2つの場合を考えてみます。速度ポテンシャルΦは、東西風(u成分)の場合は東西方向(x軸方向)に勾配を持つ一方、南北風(v成分)の場合は南北方向(y軸方向)に勾配を持ちます。
西風の場合は東西位置x、x+δxにおける速度ポテンシャルΦ(x)、Φ(x+δx)と風のu成分の関係を差分で表現し、u>0(西風)となる条件を求めます。この結果「Φ(x+δx)>Φ(x)」となり、「(風下のΦ)>(風上のΦ)」となります。
南風の場合は南北位置y、y+δyにおける速度ポテンシャルΦ(y)、Φ(y+δy)と風のv成分の関係を差分で表現し、v>0(南風)となる条件を求めます。この結果「Φ(y+δy)>Φ(y)」となり、「(風下のΦ)>(風上のΦ)」となります。
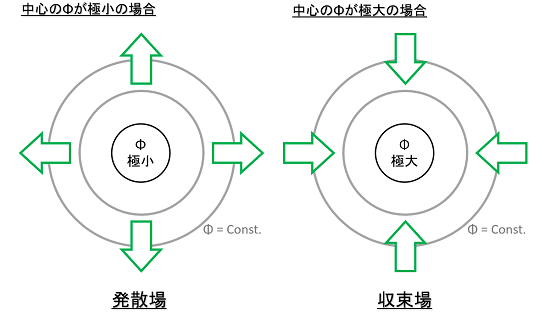
こちらの図では、速度ポテンシャルΦが同心円状に分布する場を考え、その中心がΦの極大・極小になる場合を考えてみましょう。速度ポテンシャルΦの値が低い方から高い方に風は流れるので、中心が極小の場合は、中心から周囲に向かって風が流れます(発散)。一方、中心が極大の場合は、周囲から中心に向かって風が流れます(収束)
続いて、大気は流れ関数(流線関数)Ψの高い方を右に見るように流れ、その極大・極小は高気圧性・低気圧性循環の中心を表します。また、流れの速度ベクトルの向きは、流れ関数(流線関数)の等値線(Ψ=一定,流線)に沿った(接線)の向きとなります。簡単な場を考えてみましょう。
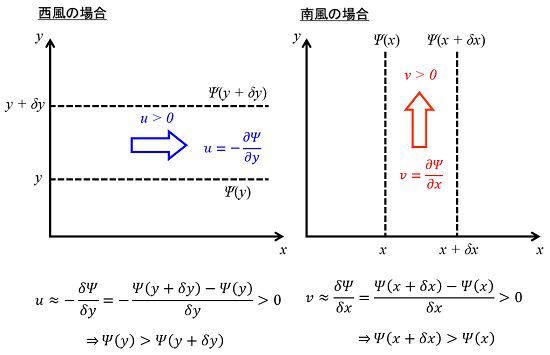
一様な西風と南風の2つの場合を考えてみます。流れ関数(流線関数)Ψは、東西風(u成分)の場合は南北方向(y軸方向)に勾配を持つ一方、南北風(v成分)の場合は東西方向(x軸方向)に勾配を持ちます。
西風の場合は南北位置y、y+δyにおける流れ関数(流線関数)Ψ(y)、Ψ(y+δy)と風のu成分の関係を差分で表現し、u>0(西風)となる条件を求めます。この結果「Ψ(y)>Ψ(y+δy)」となり、「Ψが高い方を右手に見るように」流れを生じます。
南風の場合は東西位置x、x+δxにおける流れ関数(流線関数)Ψ(x)、Ψ(x+δx)と風のv成分の関係を差分で表現し、v>0(南風)となる条件を求めます。この結果「Ψ(x+δx)>Ψ(x)」となり、「Ψが高い方を右手に見るように」流れを生じます。
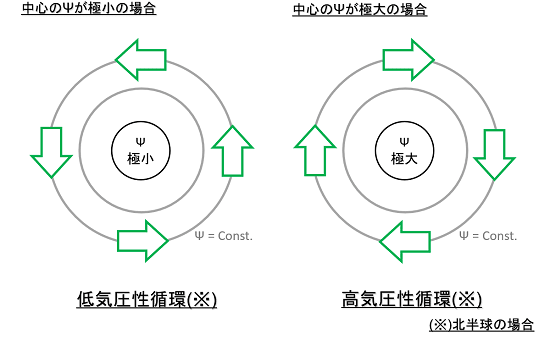
こちらの図では、流れ関数(流線関数)Ψが同心円状に分布する場を考え、その中心がΨの極大・極小になる場合を考えてみましょう。流れ関数(流線関数)Ψの値が高い方を右に見るように風は流れるので、中心が極小の場合は、反時計回りに風が流れます(低気圧性循環)。一方、中心が極大の場合は、時計回りに風が流れます(高気圧性循環)。
最後にもう一点、速度ポテンシャルの等値線と流れ関数(流線関数)の等値線は直交します。
大気は速度ポテンシャルΦの低い方から高い方に流れ、その極大・極小は収束・発散の中心を表します。また、流れの速度ベクトルの向きは、速度ポテンシャルの等値線(Φ=一定)に対して直角です。簡単な場を考えてみましょう。

一様な西風と南風の2つの場合を考えてみます。速度ポテンシャルΦは、東西風(u成分)の場合は東西方向(x軸方向)に勾配を持つ一方、南北風(v成分)の場合は南北方向(y軸方向)に勾配を持ちます。
西風の場合は東西位置x、x+δxにおける速度ポテンシャルΦ(x)、Φ(x+δx)と風のu成分の関係を差分で表現し、u>0(西風)となる条件を求めます。この結果「Φ(x+δx)>Φ(x)」となり、「(風下のΦ)>(風上のΦ)」となります。
南風の場合は南北位置y、y+δyにおける速度ポテンシャルΦ(y)、Φ(y+δy)と風のv成分の関係を差分で表現し、v>0(南風)となる条件を求めます。この結果「Φ(y+δy)>Φ(y)」となり、「(風下のΦ)>(風上のΦ)」となります。

こちらの図では、速度ポテンシャルΦが同心円状に分布する場を考え、その中心がΦの極大・極小になる場合を考えてみましょう。速度ポテンシャルΦの値が低い方から高い方に風は流れるので、中心が極小の場合は、中心から周囲に向かって風が流れます(発散)。一方、中心が極大の場合は、周囲から中心に向かって風が流れます(収束)
続いて、大気は流れ関数(流線関数)Ψの高い方を右に見るように流れ、その極大・極小は高気圧性・低気圧性循環の中心を表します。また、流れの速度ベクトルの向きは、流れ関数(流線関数)の等値線(Ψ=一定,流線)に沿った(接線)の向きとなります。簡単な場を考えてみましょう。

一様な西風と南風の2つの場合を考えてみます。流れ関数(流線関数)Ψは、東西風(u成分)の場合は南北方向(y軸方向)に勾配を持つ一方、南北風(v成分)の場合は東西方向(x軸方向)に勾配を持ちます。
西風の場合は南北位置y、y+δyにおける流れ関数(流線関数)Ψ(y)、Ψ(y+δy)と風のu成分の関係を差分で表現し、u>0(西風)となる条件を求めます。この結果「Ψ(y)>Ψ(y+δy)」となり、「Ψが高い方を右手に見るように」流れを生じます。
南風の場合は東西位置x、x+δxにおける流れ関数(流線関数)Ψ(x)、Ψ(x+δx)と風のv成分の関係を差分で表現し、v>0(南風)となる条件を求めます。この結果「Ψ(x+δx)>Ψ(x)」となり、「Ψが高い方を右手に見るように」流れを生じます。

こちらの図では、流れ関数(流線関数)Ψが同心円状に分布する場を考え、その中心がΨの極大・極小になる場合を考えてみましょう。流れ関数(流線関数)Ψの値が高い方を右に見るように風は流れるので、中心が極小の場合は、反時計回りに風が流れます(低気圧性循環)。一方、中心が極大の場合は、時計回りに風が流れます(高気圧性循環)。
最後にもう一点、速度ポテンシャルの等値線と流れ関数(流線関数)の等値線は直交します。

















