このところ極限等級について多くのコメントを頂いています。
星爺さんによれば、望遠鏡の極限等級は焦点距離のみによって
決まり、口径やFとは無関係とのことです。
吉田正太郎先生のご著書
天文アマチュアのための
望遠鏡光学・反射編
誠文堂新光社
P-48 12望遠鏡の実視極限等級
から引用します。
-------- 引用ここから ----------
望遠鏡で、やっと見える恒星の等級を、極限等級(limitting magnitude)
と言います。瞳孔径7.0mmの人が6.0等星まで見えるとすれば、
望遠鏡の極限等級Mは、つぎの式で計算できます。
M=5logφ+1.774(等)・・・・(2・24)
φの単位はmm、logは常用対数です。
以上は実視極限等級ですが、写真の場合は感光材料の種類、露出時間、
ピントの良否などにも関係するので、実測してみるほかはありません。
ただし、その星像は円形で、黒さが均一でなければなりません。
オムスビ形やコンマ形の小さな像は、星像にはかぞえません。
------- 引用ここまで -----------
P-49には、
表2.1 望遠鏡の有効径と性能の一覧表
が記載されています。
また、望遠鏡の光学的な性能は、ほとんどすべて口径によって
定まりますから、望遠鏡の大きさは口径で表示します。
たとえば30cm望遠鏡といえば、口径(有効径)30cmの望遠鏡の
ことです。
と書いてあります。
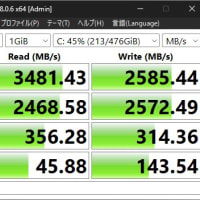
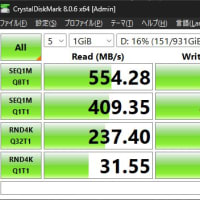
では、65cmF12と10cmF78の望遠鏡は同じ性能なのでしょうか?
<65cm望遠鏡>
分解能:0.178"角
実視極限等級:15.84等星
集光力:8622倍
<10cm望遠鏡>
分解能:1.160"角
実視極限等級:11.77等星
集光力:204倍
両者間には、5段プラスの露出倍数(43.1648倍)もの差があります。
65cmF12で600secを適正露光とすれば、10cmF78では7h10mもの時間を
要する計算です。
10cmF78の望遠鏡があったとすれば、理論的には1カット7h10m露光
すれば、65cmF12で600sec露光した時と同じ極限等級を得られる
というのが星爺さんのおっしゃられていることです。
また、
このM51は何センチの望遠鏡で撮影したのですか? ではなく、
このM51は何mm望遠レンズで撮影したのですか?
と聞くようになることが必然だと言うことです。
確かにカメラの世界では、このF22は何ミリ望遠で撮りましたか?
のような聞き方をしますね。
しかし望遠鏡の世界では、このM51は何センチの望遠鏡で撮りましたか?
と聞きます。
論点は、
焦点距離が同じ場合、適正露光であれば極限等級は同じであり、
得られる結果は同じである・・・
と言う点です。
星爺さんのコメントに、
>星や銀河自体のフォトン数が重要なのは当然です。
>銀外自体とは=単位面積ということですね。
>星は点像なので口径が大きいと短時間露出でも良く
>写りますが、飽和まで露出する(=適正露出)場合は
>口径が小さい(=Fが暗い)とバックグラウンドが暗い
>ので飽和までの露出時間を長くでき、結果として
>最微光星は焦点距離が同じなら同じになります。
>露出が不足した場合は面積体は良く写らないで星ばかり
>写ります。こうした写りの状態を見て
>「大口径は良く写る」と感じやすいのでしょうかね?
>例の公式は、相反則不規のないデジタルになればより
>算数になるので、結果はより正直で理論と現実の乖離は
>フィルムよりも少なくなります。
>これらの概略がどういうことかというと、
>①口径が大きいほど良く写って
>②露出が長いほど良く写って
>③焦点距離が長いほど良く写ります。
>すなわち、望遠鏡の大型化は永遠のテーマです。
>が、①②③は相関関係にあるということです。
とあります。
ハイ、「大口径は良く写る」と感じます。
それは、65cm鏡の場合8622倍もの集光力があり、
7800mmという超々望遠レンズでもF12という現実的な明るさ
を得られるからです。
また、最近の画像処理技術の進歩により、
日本のシーイングでも、前出のM51程度の画像はアッサリ撮影できて
しまうというブレイクスルーもあります。
”日本のシーイングでは1”角以下は期待できない”
”日本のシーイングでは30cm以上の口径は無意味”
本当でしょうか? 様々な画像復元処理法、
ラッキーイメジングやスペックル干渉法によって、
もはやそのような常識は崩れました。
やはり、望遠鏡は口径が大切です。
口径が大きければ、結果的に焦点距離が伸びて限界等級も上がり、
現実的なF値に収まって、実用性が確保できるのです。
焦点距離が同じ場合、適正露光であれば極限等級は同じであり、
得られる結果は同じである・・・
これは正しい理論かもしれませんが、10cmの分解能は1.160"角です。
6cmでは1.933"角しかありません。
大口径、長焦点、明るいF、微細撮像素子、補償光学系、
様々な画像復元処理を使えるならば、口径こそ望遠鏡の性能指標
という考え方は間違っていないと思います。
星爺さんによれば、望遠鏡の極限等級は焦点距離のみによって
決まり、口径やFとは無関係とのことです。
吉田正太郎先生のご著書
天文アマチュアのための
望遠鏡光学・反射編
誠文堂新光社
P-48 12望遠鏡の実視極限等級
から引用します。
-------- 引用ここから ----------
望遠鏡で、やっと見える恒星の等級を、極限等級(limitting magnitude)
と言います。瞳孔径7.0mmの人が6.0等星まで見えるとすれば、
望遠鏡の極限等級Mは、つぎの式で計算できます。
M=5logφ+1.774(等)・・・・(2・24)
φの単位はmm、logは常用対数です。
以上は実視極限等級ですが、写真の場合は感光材料の種類、露出時間、
ピントの良否などにも関係するので、実測してみるほかはありません。
ただし、その星像は円形で、黒さが均一でなければなりません。
オムスビ形やコンマ形の小さな像は、星像にはかぞえません。
------- 引用ここまで -----------
P-49には、
表2.1 望遠鏡の有効径と性能の一覧表
が記載されています。
また、望遠鏡の光学的な性能は、ほとんどすべて口径によって
定まりますから、望遠鏡の大きさは口径で表示します。
たとえば30cm望遠鏡といえば、口径(有効径)30cmの望遠鏡の
ことです。
と書いてあります。
では、65cmF12と10cmF78の望遠鏡は同じ性能なのでしょうか?
<65cm望遠鏡>
分解能:0.178"角
実視極限等級:15.84等星
集光力:8622倍
<10cm望遠鏡>
分解能:1.160"角
実視極限等級:11.77等星
集光力:204倍
両者間には、5段プラスの露出倍数(43.1648倍)もの差があります。
65cmF12で600secを適正露光とすれば、10cmF78では7h10mもの時間を
要する計算です。
10cmF78の望遠鏡があったとすれば、理論的には1カット7h10m露光
すれば、65cmF12で600sec露光した時と同じ極限等級を得られる
というのが星爺さんのおっしゃられていることです。
また、
このM51は何センチの望遠鏡で撮影したのですか? ではなく、
このM51は何mm望遠レンズで撮影したのですか?
と聞くようになることが必然だと言うことです。
確かにカメラの世界では、このF22は何ミリ望遠で撮りましたか?
のような聞き方をしますね。
しかし望遠鏡の世界では、このM51は何センチの望遠鏡で撮りましたか?
と聞きます。
論点は、
焦点距離が同じ場合、適正露光であれば極限等級は同じであり、
得られる結果は同じである・・・
と言う点です。
星爺さんのコメントに、
>星や銀河自体のフォトン数が重要なのは当然です。
>銀外自体とは=単位面積ということですね。
>星は点像なので口径が大きいと短時間露出でも良く
>写りますが、飽和まで露出する(=適正露出)場合は
>口径が小さい(=Fが暗い)とバックグラウンドが暗い
>ので飽和までの露出時間を長くでき、結果として
>最微光星は焦点距離が同じなら同じになります。
>露出が不足した場合は面積体は良く写らないで星ばかり
>写ります。こうした写りの状態を見て
>「大口径は良く写る」と感じやすいのでしょうかね?
>例の公式は、相反則不規のないデジタルになればより
>算数になるので、結果はより正直で理論と現実の乖離は
>フィルムよりも少なくなります。
>これらの概略がどういうことかというと、
>①口径が大きいほど良く写って
>②露出が長いほど良く写って
>③焦点距離が長いほど良く写ります。
>すなわち、望遠鏡の大型化は永遠のテーマです。
>が、①②③は相関関係にあるということです。
とあります。
ハイ、「大口径は良く写る」と感じます。
それは、65cm鏡の場合8622倍もの集光力があり、
7800mmという超々望遠レンズでもF12という現実的な明るさ
を得られるからです。
また、最近の画像処理技術の進歩により、
日本のシーイングでも、前出のM51程度の画像はアッサリ撮影できて
しまうというブレイクスルーもあります。
”日本のシーイングでは1”角以下は期待できない”
”日本のシーイングでは30cm以上の口径は無意味”
本当でしょうか? 様々な画像復元処理法、
ラッキーイメジングやスペックル干渉法によって、
もはやそのような常識は崩れました。
やはり、望遠鏡は口径が大切です。
口径が大きければ、結果的に焦点距離が伸びて限界等級も上がり、
現実的なF値に収まって、実用性が確保できるのです。
焦点距離が同じ場合、適正露光であれば極限等級は同じであり、
得られる結果は同じである・・・
これは正しい理論かもしれませんが、10cmの分解能は1.160"角です。
6cmでは1.933"角しかありません。
大口径、長焦点、明るいF、微細撮像素子、補償光学系、
様々な画像復元処理を使えるならば、口径こそ望遠鏡の性能指標
という考え方は間違っていないと思います。
























お手数とは思いますが、片方を消してください。>☆男さん
長々と議論してしまいましたが、調べる中で色々と勉強になりました。
また基本的な部分を勉強し直してみます。
皆さんありがとうございました。
後半をお送りします。
私はここ数年で天文を始めた(正確には30年ぶり位の再開)ので小惑星の話は存じませんが、小口径シュミットカメラの成果ということであれば焦点距離が短いぶん写野が広いことがアドバンテージになったのでしょうか。
シュミットカメラは憧れでしたが、今はかえって手に入れにくくなりましたね。自分も使ってみたいとは思っていましたが、機会はなさそうです。
結局言いたいことは、焦点距離が限界等級に及ぼす影響は大きいと思いますが支配的ではなく、露出時間や口径も寄与するということです。
北杜の犬さん、
回折限界は、エアリーディスクを調べて見るといいかと思います。
この大きさは、半径 r=1.22λFです。
2r=1.22Fの式は、0.5umの波長で計算したものでしょう。
回折もなかなか面白い現象ですよね!
>なので露光時間が長いほど、口径が大きいほどS/Nに寄与するわけです。
全く当然です。同感です!
これに撮影の能率(露出時間を短くする)を加味すればFの明るいシュミットカメラが能率が良
いので、どんどん大きくり世界中の主な天文台には大型のシュミットカメラがあります。
フィルムよりも解像力の高いデジタル時代になって、シュミットカメラの性能向上が課題になり、
世界中の大きなシュミットカメラの補正板がアクロマート色消しになりました。単レンズ補正板
なのは木曽観測所のシュミットカメラくらいです。
私がシュミットカメラを使うのをやめたのは、初心者のために、
・デジタル時代は相反則不規がないので長時間露出が可能。
・それならばFの暗い望遠鏡でも使える(露出時間は長いが)。
・極限等級も分解能も焦点距離に依存するので小口径望遠鏡で良い。
-----以上を実践して示す(前のコメントのM106がその例)ことが急務だ。
と不遜ながら考えたことと、小型のシュミットカメラでもデジタル機器にはアクロマート補正板
が必要になって、これの製作が難しくなったからです。
フォトンの量については光の量ですから、今まで説明させていただいた理屈と同様にFや口径の
分解能に伴った撮像素子の解像度が基本で、星像に投じられるフォトンの量が決まります。
適した言葉がなかったので、「適正露出」とか「飽和まで露出」を用いましたが、これがいけな
かったですかね? 「Fの明るさに応じた露出」とすればよいでしょうか?
同じ焦点距離のF4とF8の望遠鏡を使ったとして、F8はF4の4倍の露出で「適正露出」になり
ます。したがって、星像に投じられるフォトンの量はF4もF8もは同じになるので、S/Nも同
じになるため極限等級も同じになります。
星爺さん、
一応、適正露出は理解しているつもりで、その先の議論をしていたつもりなのですが...。
昨今のデジタル天体写真で「適正露出」で多数枚撮影し、それらを積算するのが主流になっていて、この積算によって適正露出の枠を超えて露出時間を増やすことができているのはご存じのとおりかと思います。
つまり一枚の写真中で露出不足の天体でも、積算により信号強度が上がってS/Nが改善します。結果、限界等級も上がるでしょう。
フォトンカウンティングの話を、どの程度考えられているかわからないので、念のため例を挙げておきます。
--------------------------------------
ざっくり0等星からの1秒間、1m^2に到達するフォトン数を10^10個程度とすると、光子数は+5等級で1/100になるので以下のようになります。
0等級 10~10フォトン/(秒・m^2)
5等級 10^8 フォトン/(秒・m^2)
10等級 10^6 フォトン/(秒・m^2)
15等級.10~4 フォトン/(秒・m^2)
20等級 10^2 フォトン/(秒・m^2)
25等級 1 フォトン/(秒・m^2)
C-14の開口を0.09m^2、光学系の伝達率を0.9と仮定すると、20等級で 8.1フォトン/秒、25等級では0.081フォトン/秒程度が到達します。因みに話に出ている23等であれば0.52フォトン/秒になります。
さらに光子を電子に変換する効率(QE)、対象像は複数ピクセルにまたがるので、限界等級辺りではまさに数十個レベルのフォトンカウンティングの世界になるわけです。
なので露光時間が長いほど、口径が大きいほどS/Nに寄与するわけです。
難しい物理ではありません。
それに伴いほとんどが拡大縮小(コピー機の拡大縮小をイメージで)計算で
きる世界です(波動光学という分野もありますが)。
なので、たいていの概算は暗算で済んでしまいます。
口径の理論分解能は、例えば口径10cmの1.16″を覚え口径が変わったら暗算。
口径の(角度の)理論分解能が見えるまで強拡大しない星野写真は、基準が
撮像素子の解像力になるので、それよりも小さな星像は無意味です。
すなわち、星像「F×1.22(μm)」が解像力より小さい必要はありません。
・眼視の高倍率には使えない やや悪い望遠鏡でも実用になります。
・F15以上くらいから撮像素子の解像力より星像の方が大きくなります。
でも、なんだかんだ言っても星像の元は点像なので事情が違いますが、それ
でも結果はそんなに違わないというのが「極限等級は焦点距離で決まる」と
いう結果で、例の計算式です。
解像力も焦点距離で決まります。が、これは長い望遠レンズの方が被写体が
大きく写って細部まで見るからで一般写真と同じですね。
十数年の撮像素子の性能が低かった頃の作品ですが下記にUPします。
未発表のもので、☆男さんの2018/3/22のブログと同じM106です。
Celestron C14に自作4枚玉レデューサーでF7です。
https://drive.google.com/file/d/1kf8qkz4TzgpzHsqOkBY7b4HABF6AeuH3/view?usp=sharing
回折限界=直焦点の原寸像の大きさ=d線の場合「F×1.22」(単位はμm)
という式は面白いですね。回折限界の大きさを15μmに固定した場合、F数も固定されますが、するとこれよりも長いF数よりもこの固定されたF数の方が暗い星が写ることになります。大気圏内では夜天光や都市の明かりの影響がありますが、宇宙空間ならバックグランドノイズが圧倒的に低いでしょうから短い=明るいF数で暗い星まで写りますね!地上での撮像とは逆です。
貴殿ブログからお体の状態を存じ上げております。どうぞご自愛下さい。
☆男様
有意義なブログを立ち上げて頂きありがとうございました。大変勉強になりました。
再読していただければ説明している箇所が見つかると思います。
これも非常に基本的なことですが、これもつまるところFと同じです。
星像が同じ大きさであった場合(例えば15μm)、Fが暗ければそれに応じて、
・星像も暗くなるけど
・バックグラウンドも暗くなる
----つまり暗い分だけ長時間露出をかけられるので、露出しただけ星像の光が蓄積
されてバックグラウンドが同程度になれば極限等級は同じになります。
このことを「適正露出」とか「飽和するまで」とか表現したのですが、余計に誤解
を招いたか? あまり難しく考えないでくださいね。
Fの暗い光学系では「露出時間がかかるので面倒くさい」です。
でも、露出時間以外は、ピント合せや光軸など楽になることが多いんですよ。
小口径でも焦点距離が同じなら、極限等級も像面の分解能も同じなので、どんどん
使うべきです。
それでは、焦点距離だけで極限等級が決まるという、星爺様の当初の理屈が成り立たなくなりますが...。
何回か同様なことを書いているように、撮像素子の解像力が根本になります。
一般的な撮像素子で1画素5μmで解像力が3×3画素の9画素分の15μmになるとする
と星像は15μmより小さくは写りなりません。15μmより大きければそのまま写ります。
・65cmF12 回折限界=14.64μm
・10cmF78 回折限界=95.16μm
これがそのまま写ります。F12は無駄のない星像ですね。
ですから、F15くらいがざっくりと暗さの上限かな? とこれも以前に書きました。
10cmF78は大きくボケて薄れて写るので極限等級は大幅に下がります。
ボケて写った単位面積あたりの光量はFと同様の概念で暗算できますから簡単。
星像直径で6倍ほど薄れていますね。それが何等星の差になるかは、1等星の差は
2.56倍ので、こちらも暗算レベルです。
回折限界=直焦点の原寸像の大きさ=d線の場合「F×1.22」(単位はμm?)とするならば、
65cmF12 回折限界=14.64
10cmF78 回折限界=95.16
となって、明らかに65cmF12のほうが星像が小さく、同じ明るさの星なら単位面積あたりの光量が大きいわけですから、10cmF78よりも65cmF12の方が暗い星まで写るのでは?単位をナノメートルとすれば撮像素子の大きさより小さくできますが、考えづらいので。
信じて挑戦してくれた人達がたくさんの小惑星を発見したことはご存じだと思います。発見の最小口径は12cm反射でした(笑)
小口径でも発見できる理屈は、ここでお話している内容と同じです。そのうえで小惑星は日々運動で流れて薄れて写ってしまう(固定撮影のようなもの)ので、流れの写らない焦点距離の短い小さな望遠鏡は有利なのです。
露出を短くして小惑星の流れを写らないように、焦点距離を長くして極限等級を向上させるように、25cm~30cm F2.6のシュミットカメラを自作して熱心な天文ファンに提供しました。何千個も発見した人います。二十代の頃の良い思い出です(笑)
シュミットカメラは像面が弯曲(通常の望遠鏡とは逆の凸弯曲)していますが、フィルムの場合はかえって好都合で平坦化レンズ無しでフィルムを凸状にピンッと張ってピントが非常に安定しました。
撮像素子は平坦化レンズが必要ですが設計は簡単です。老眼鏡のレンズを代用したこともあります。
最近話題のRASAという口径28cm F2.2シュミットは、補正板を正規の位置よりうんと近くに配しているので、像面弯曲に伴って強烈なコマ収差と若干の非点収差が発生します。これを補正レンズで解消しています。高い光学設計技術と思います。
シュミットカセグレンの副鏡を外してカメラを取付けるハイパーなんとかというのもありますね。補正板のパワーが10%ほど不足なので上記に加えて負の球面収差も発生します。それらを全部補正するのですから、さらに高い技術です。日本は遅れていて残念に思います。
普遍的なとっても簡単な基本の理屈をお話しているだけですが「大口径は有利という先入観(?)は、こんなに激しいものなのか? と改めて思います。
別のアプローチからお話します。一般写真を想像してください。
Fが同じなら露出時間は同じ----これは理解できますよね?
Fが明るいと口径が大きいから解像度が上がる----わけないですよね?
Fに応じた適正露出をすれば----得られる写真は同じですよね?
Fとはレンズで集められた光が「ある大きさに集光する」口径比だから、Fが同じなら撮像面の光は同じ明るさになります。
実は星でも同じことで「ある大きさに集光する」のです。ある大きさは撮像素子の解像度で決まります。なので例の計算式でも星像直径を代入します。要するにFの概念と全く同じなわけです。
撮像素子の解像力は通常のカメラなら15μmと仮定すれば良いと思います。当然ながらもっと詳細な撮像素子なら解像力が上がって詳細に写り極限等級も向上します。
ただし、シーイングで星が膨れると「ある大きさに集光する」星像が広範囲になってボケて解像力が下がり同時に光が薄れて極限等級は落ちます。
考え方はそのスタンスが良いと思います。
経験則だとすると、「基本の理屈」とは言えないと思うのです。
星爺さん、
「写真の極限等級は焦点距離に依存する」で一点教えてください。
「あるF値で、極限等級に達するまでの時間」です。
※以前のコメントでは適正露出と記載されていたと記憶してます。
ところでシュミットカメラですが、これはフィルム用ですか?
像面を湾曲(球面に?)させせ撮像しないと良像は得られませんよね?
その場合はデジタル化は難しいとは思いますが、興味あります。
アマチュアのための望遠鏡光学
とは言え、数式がある以上は定量的に追求したいですね。
シッポのlog・dのdをどう理解するかで結果が変わります。
すばるはプロ機、我々はアマ機使いです。
アマの望遠鏡光学ではこの程度で良いのだ!
と言うなら、現在のアマには通用しないでしょう。
大望遠鏡レベルのプロ機ではもっとシビアであり、
そうそう簡略化した式では表せませんが、
我々アマチュアが扱う望遠鏡では、この式で考えて
問題はありません。と言った感じが落としどころで
しょうか?
露光を1分以下にしたい私としては、
口径を大きくして、Fを小さくして、コマコレで悩んで、
写ったど~~!って喜んでいるのが現状です。
65cmF12は7800mmmもの超々望遠レンズですから、
結果的に凄いのが撮れたと思っても間違いではありませんよね?
これが32.5cmF24だったら、現実的な時間内、機械精度の
問題もあって使う気にはなれません。
よって、望遠鏡が大口径化するのは必然だと思います。
デジタルだと15μmと言うのも今ひとつ理解できません。
F×1.22でF8なら9.76μmであり、2.4μm画素のカメラなら
4×4画素も使えて画像処理がやりやすいし、もちろん
十分に解像していると思うのですが。
大学の応用光学の授業で習っただけのズブの素人です。しかも機械系です(笑)。
ですから、工学部出身者はレンズの本質がフーリエ変換器ということは知っているのが当たり前だとずっと考えていたのですが違うのですね。これには少し驚きました。
星爺様
”直焦点の原寸像の大きさはd線の場合「F×1.22」”ということで、星像の大きさの式は分かりました(ただし、チェックのために導出過程には興味があります)が、星像の明るさはどうでしょう?積分範囲が大きくなる以上、口径が大きい方が情報量が増す気がするんですが。
どなたか、光学の専門の方のご教授を頂きたいところです。
私はアマチュアの望遠鏡の一般論をお話しているのであって、専門家の機材では異なることはあると思いますよ。基本はまったく同じなのですけれど。
申し上げたいのは、こうした基本の理屈を理解していないと、撮影用望遠鏡の選択を間違えてしまいそうなことです。
例えば、25cm F4のニュートン反射があったとします。ユーザーは惑星撮影の望遠鏡とごっちゃにして「星野写真も大口径が必要だ!」だから「25cmの口径は譲れない!」と、F4に対応するコマコレの良いのが必要。光軸調整が大変。ピント合せがとても難しい。とか、なんだかんだと苦労していたとします(これはこれで楽しいが)。
その25cm反射を15cm(F6.6)に絞ったら----あら不思議! 露出時間は2倍半ほどかかるが、コマ収差は1/3近くに減って一見わからない。像面弯曲は同じだが焦点深度が深いので周辺像もまあまあ。斜鏡の割合が大きくなって周辺減光も解消。ピンと合せはルーズでOK。そのうえ撮れた写真は極限等級も星雲などの解像度も変わらない。
こうなると漫画みたいですよね? 最初から15cmでも良いですし。
『天文ガイド』が中学生を読者と定めて、難しそうな理屈の記事を敬遠していたためと思いますが(私の責任でもある)、最近は著者や指導的立場の人でも基本のわかっていない人がいて、これは困った、とちょっと焦ってコメントもたくさん書いてしまいました。お目汚し失礼しました
件の計算式のすばる望遠鏡への適用ですが、
星像を0.7秒角(f=16400mmの場合、星像直径で55.66um)として以下のように計算しました。
mL = 1.38 + 5 * log(16400) - 2.5 * log(16400 * sin(0.7/3600))
= 約25.6
星爺さん、
下記URLの"Public Data Release 1"に実限界等級とターゲットの限界等級の記載があります。F2という明るい光学系でも露出時間をかけると限界等級が上がることが判ります。
https://hsc-release.mtk.nao.ac.jp/doc/
また件の式と上記データと比較すると、式の性格が見えてきます。
特に星像の直径dは多数のパラメーターから決まるものと考えられるので、実測ベースの式と予測され、理論ベースの式からは相当簡略化されているのでしょう。
もっともアマチュアレベルの機材であれば、ある程度はマッチするという考えもあるのは理解しています。
この辺りをご理解頂ければ、件の式を基に「写真の極限等級は焦点距離で決まるんですよ」とは言えないのではないでしょうか?
北杜の犬さん、
レンズのフーリエ変換! 専門家でしょうか?
レーザーなどのコヒーレント光を通すと面白いですよね!?
学生時代を思い出してしまいました。でも今は全然わかりません(汗)
大口径が有利と考えがちな原因は、回折限界の分解能が必要な惑星や二重星の高倍率観測の経験から来るものだと思います。
回折限界は口径に比例して良くなるわけですが、直焦点像も当然比例して大きくなるので、つまりFが同じなら直焦点の原寸像は口径や焦点距離にかかわらず同じ大きさです。これは重要なポイントかも?
直焦点の原寸像の大きさはd線の場合「F×1.22」になります。
Fが明るいとシャープな直焦点像を結びます。が、しかし、直焦にいくらシャープな像を結んでも、撮像素子の解像力よりシャープには写りません。撮像素子の解像力は15μmとするのが妥当なところですから(諸説あり)、直焦点に15μm以下の非常にシャープな星像が投影されても、星像は15μm以下にななりません。ここも重要なポイントかも?
フィルム時代は相反則不規でFが明るくないと星野は写らなかったので、その経験が大口径礼賛になっているのかも。ここも重要なポイントですかね?
相反則不規のないデジタルカメラなら、Fが暗くても露出時間を増やせば写ります。最近はFの暗い光学系を積極的に星野に使うことを啓蒙しています。でも、口径が大きくないとダメだと思う人は多いみたいです。
30年前は自作のシュミットカメラばかり使っていました。デジタルになってFの暗い光学系を使わないと“損”だと思っていますが、撮影の能率を考えるとFの明るいのは良いですね!
拙宅に25cm F2.2と30cm F2.6 シュミットのボロボロなのがありますが、整備してお使いになりますか?
おお、そう言えば最近公開されていましたね!
まだ見に行っていませんでした。粉銀河マニアにはたまらない情報箱です。
早速ブックマークして読んでます。
えーっと、
>因みに件の計算式(星像を0.7秒角と仮定)で25.6等となりました。
>g線でWltraDeepが27.4等なので結構乖離がありますね。
私が計算したら22.84等になっちゃいました・・・アレ?
ひえ~、レンズがフーリエ変換器とは考えたこともありませんでした。
皆さん素晴らしい頭脳をお持ちのようで・・・
音響光学などの授業で少しカジッタことはありますが、あの、FFTってやつですよね。
工学の世界と理学の世界を混ぜて追及しないと分からない問題かもしれません。
学術論文などは読む機会がないのですが、すばる望遠鏡などでも観測結果を優先
しているみたいですね。論文に書く場合にも、理論モデルで数値が変化するような
書き方はせず、観測結果に基づいて定量的な記述をするとか。
mL=1.38+5log f-2.5log d
という公式を見て、多分に観測結果を反映した経験則とか、実測値などと見抜ける
頭脳は凄いですね。
縮小光学系で撮ると明るさが凝縮され、フーリエ変換が効率よく・・・積分され・・
う~ん、付いて行けない(ノД`)・゜・。
何度も同じようなことをお聞きしてスミマセン。
ご丁寧に教えて頂き感謝を致します。
デジタル時代の現実的なF値が15付近と言うのは、全くその通りだと感じます。
6cmF20だと星像が大きくなる件もナルホドです。
DSO狙いでは、如何に恒星像を小さく表現できるかと言うことも重要だと
感じております。すばる望遠鏡などの大型機では、本当に恒星像が小さく美しい。
その上で、DSO天体がうじゃうじゃ写っている。
35.5cmF11のC-14は個人的に深銀河撮影を行ったり、超新星観測をやるには丁度良い
大きさだと思い始めました。F78とかF20の話しをしていたら、F11がもの凄く明るく
思えて来ました(^^♪
すばる望遠鏡で良い資料を見つけました。
https://prc.nao.ac.jp/citizen-science/hscv/hscdata.html
(このサイト先日公開されたばかりですがなかなか楽しいです)
HSCの主焦点(f=16.4m)だと、"観測波長と限界等級"の記載があります。
Wide/Deep/UltraDeepで露出時間の違いで限界等級に違いがあるので、すばるのF値(2.0)をもってしても現実的な露出時間(というには長いですが)では限界等級の飽和はないということがわかると思います。
因みに件の計算式(星像を0.7秒角と仮定)で25.6等となりました。
g線でWltraDeepが27.4等なので結構乖離がありますね。
HSCビュワー! お勧めです!!!
http://hscmap.mtk.nao.ac.jp/hscMap2/
式の掲載ありがとうございます。
mL=1.38+5log f-2.5log d
fは焦点距離
dは星像の直径
式を拝見するにどうも経験則のようですね。dは実測値なのでしょう。
繰り返しになりますが、レンズ(鏡も含め)はフーリエ変換器です。フーリエ変換は-∞から+∞まで積分しますが、有効な範囲は当然、レンズの大きさである直径です。積分範囲が変われば当然、フーリエ変換後の関数、つまり、星像の直径や明るさに影響します。口径が変わっても解が一つにしかならないなら口径に依存しないことになりますが、果たしてそうなのでしょうか?
光を捉えるまでの状態が分かればあとは撮像素子の問題になるので、是非とも像の直径、明るさと口径の解析的な関係式を知りたいものです。
計算式を拝見してある程度納得。
途中の計算式が判らないので推測ですが、理論値からの導出ではなくて実測ベースの式でしょうか。この式で注目すべきはd(半値全幅で単位はmm?)で、これがかなり効いています。またdは口径なども影響するので、最微等級が焦点距離で決まるとは言えないでしょう。
また考えていただきたいのは最微光星の適正露出とはなんぞや? ということです。最微光星は識別できる際ですから露出不足ですが、これを適正露出にもっていくとすると、その過程でさらに暗い最微光星が検出できます。
ところが最微等級付近では時間当たりのフォトン数が極端に少なくなるので、SignalがNoiseに埋もれやすくなります。そうすると長焦点ではSignalを狭い範囲(画素や感光材粒子)に押し込めることができるので有利(支配的と言えるかまでは疑問ですが)になるのでしょう。
6cmの分解能は1.933"角、20cmの分解能は0.580"角になりますね。
角度の分解能が撮像素子上に投影されますが、こちらは「実寸の分解能」と言いましょう。焦点距離にかかわらず F×1.22の大きさに投影されるので、6cm F20の実寸の分解能は24.4μmで20cm F6の実寸の分解能は7.32μmです。極限等級も像の分解能も撮像素子(フィルム)の解像力と投影される星像直径で決まります。
フィルム時代なら解像力は30μmと仮定されたので、その時代なら6cm F20と20cm F6は双方とも30μm以下で投影される星像のため写る星像の大きさは30μmです。絞りボケ(6cm F20に注目)がフィルムの解像力より大きくないからです。なので飽和まで露出をしたら全く同様の写りになります。Fが暗いと撮影の能率は著しく悪いですけれど…。
デジタルの撮像素子の解像度をフィルムの2倍の15μmと仮定すると、6cm F20は撮像素子の解像力よりも大きな24.4μmの星像を投影して「ややピンボケ」に写ります。20cm F6は7.32μmの星像を投影しますが、撮像素子が解像しないので15μmに写ります。したがって極限等級は20cm F6が0.8等星ほど上回ります。星雲など面積体の分解能は言わずもがなですね。
デジタル時代はF20では少しボケて写るので苦しいです。前出のINOUEさんの作例、
http://photozou.jp/photo/show/177665/238175956
は、このことがよくわかり少し眠い感じですね。INOUEさんは承知の上でF20で撮っています。
使用する撮像素子の解像力によって変わりますが、私はざっくりと「F15くらいがデジタル時代の暗いFの上限かな?」と思っています。
※当然ながら、これらのお話は光学系の出来やシーイングは考えに入れない場合です。
mL は magnitude Limit で宜しいでしょうか?
一般写真での”回折ボケ”は知っていますし、10cmF78など有り得ない例を出して、
余計にメンドクサイ話になって恐縮です。m(__)m
星野写真と眼視の高倍率や惑星写真の分解能を同列で論じる人が多いことは確か
ですね。私も今回のM51画像に木星を貼り付けてみれば、大した分解能では
無いことがわかる筈です。。。とコメントしています。
要するに、
ものには限度と言うものがあり、DSO狙いで4000mmの焦点距離が欲しければ、
Fが明るいに越したことは無い。1mF4プライムと書いたのはソコです。
現実的な40cmF10カセグレンよりも短時間(撮影に使える時間は有限ですから)で
結果を得られます。短時間で適正露出を得たいならば、当然にFが明るい方が良い。
なので、一般的には大口径の方が良く写る(早く適正露出まで持って行ける)と
言う訳です。
1カット10分でも長いと感じる現在では、尚さらにそうでしょう。
40cmF10でも、1mF4でも、適正露光ならば同じ結果になる。
mL=1.38+5log f-2.5log d
はそのような式ということですね。
では大気や外乱が無いとして、6cmF20と20cmF6は同じでしょうか?
6cmの分解能は1.933"角、20cmの分解能は0.580"角です。
この式には口径による分解能の違いというファクターが抜けていると思うのですが、
本当にこれが正しいのでしょうか?
「写真の極限等級は焦点距離で決まるんですよ」
「へーっ、そうなんだ~」
で済む話と思って詳しい記事を展開しませんでしたが、大口径ほど暗い星が写ると思っていたり、星野写真と眼視の高倍率や惑星写真の分解能を同列で論じる人が多いことに気がついて、ちょっと焦っています(笑)
眼視の極限等級の計算式は見たママですが、写真ではFが暗いと露出を長くできるので当然ながら計算式は全く異なります。
H先生が改善した計算式の元原稿があったのでご紹介します。
要約した計算式の結論だけ示します。
mL=1.38+5log f-2.5log d
fは焦点距離
dは星像の直径
望遠鏡の口径や撮像素子の感度は無関係。同じ焦点距離で口径が小さくなると星の光を集めにくくなるがFが暗くなるためバックグランドも暗いので露出を長くできて極限等級は向上する。
星像直径はシーイングで変わりますが適当な数値で良いと思います。
----以上です。
口径が大きいほど光子を集められることは直感的にも肌感覚でわかりますが、分野は変わりますが、境界要素法で熱伝導をシュミレートするときは、領域全体の要素の影響を支配関数で積分していきます。要するに、星像とはレンズの部分部分の効果を積分(寄せ集めたもの)したものと思われますので(なんとなれば、光学系はフーリエ積分器なので)、撮像素子が検出できる星の明るさ/暗さは口径に依存するのではないでしょうか?
星爺様の仰る焦点距離だけに依存する式を教えて頂けませんでしょうか?もしその式が経験即から導出されていれば、撮像素子の発展している現在に対応できているのか問題がありますし、もし波動関数から解析的に導かれているものならば信用できると思います。その際は、我々が常識と捕らえている感覚が実は間違っていることになりますが、物理の世界ではよくあることです。
星野の直焦点写真は撮像素子の解像力が根本なので、通常は「角度の分解能」いわゆる回折限界まで撮像素子は解像しません。撮像素子の解像力と星像のあいまった分解能になります。これをとりあえず「実寸の分解能」と呼びましょうか。
例えば、F4の望遠鏡の「角度の分解能」は、撮像素子上の「実寸の分解能」では4.8μmほどになります。撮像素子の星像の解像力はフィルムだと現実的な数値では30μmくらい、デジカメの撮像素子では2倍シャープな15μmとしましょう。すると、F4の望遠鏡は4.8μmのシャープさは不要で、4倍近く結像の悪いちょっと不良なものでも使えます。
◆65cmF12と10cmF78の望遠鏡は同じ性能なのでしょうか?◆
とあったので引用すると、F12は撮像素子上の実寸の分解能は15μmくらいです。高倍率の眼視に耐える結像性能があれば無駄なくちょうど良いFですね。F78になると撮像素子上の実寸の分解能は95μm(0.095mm)にもなり甚だしいピンボケです。ピンホールカメラに近付いてゆくからです。35mm判ならパソコンディスプレイに投影する星像は1mmほどになってしまいます。眼視なら低倍率アイピースをで口径10cmの適正倍率にすれば良いのですけれど。
このように、あまりにも小口径で長焦点(Fが暗い)にすると星像の集中度が下がるので星は星雲のようにピンボケみたいに写って極限等級は向上しません。焦点距離に見合ったFが必要なのです。
一般写真でもF22くらいまで絞ると明らかにピントが甘くなります。高性能なデジカメだとF16でもわかります。一般写真の世界では絞り過ぎによる「絞りボケ」と言われます。
星野写真では、まぁ、だいたいF10くらいまでが良いのかな? と思います。もちろん少し甘くなるのを承知でF20はアリと思います。
面積体と違って恒星は点像なので少し事情が異なりますが、結局は最微光星の写りは「適正露出」をすれば口径にもFにも無関係で焦点距離のみに依存するというのが例の公式です。キーワードは適正露出で飽和近辺まで露出して性能を引き出すということです。
経験的に大口径が良く写ると感じるのは露出不足の場合でしょう。眼で見る場合は瞬間的な光量を眼で捉えるので口径が大きいほど暗い星が見えます。露出不足だと上記の飽和に達しないので、眼で見る状態に近くなって点像の星は大口径ほど写りやすくなります。