『三角形の二辺の和は一辺に等しい』の意ですが、その証明は次のとおりです。
一辺が1の正三角形を用意し、それぞれの頂点をA、B、Cとします。
辺ABと辺ACのそれぞれの中点から底辺BCの中点に向かって線を引きます。
そうすると、
ABとACの和(1+1)と新たにできた二つの小さい正三角形の底辺以外の和が等しくなります。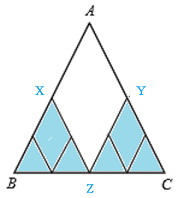
AB、AC、BCの中点をそれぞれ、
X,Y,Zとすると、
AB+AC=BX + XZ + ZY + YC
その後、同じようにそれぞれの新たな小さい正三角形が
今度は4つできます。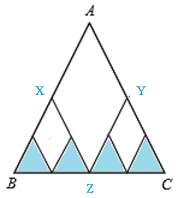
この底辺以外の辺の和とAB+ACの長さが等しくなります。
これを延々に続けると。。。無限の三角形が出来上がり、
三角形ABCの辺BCと同じになります。
つまり、AB+AC=BC
1 + 1 = 1
と なるわけです。
一辺が1の正三角形を用意し、それぞれの頂点をA、B、Cとします。
辺ABと辺ACのそれぞれの中点から底辺BCの中点に向かって線を引きます。
そうすると、
ABとACの和(1+1)と新たにできた二つの小さい正三角形の底辺以外の和が等しくなります。

AB、AC、BCの中点をそれぞれ、
X,Y,Zとすると、
AB+AC=BX + XZ + ZY + YC
その後、同じようにそれぞれの新たな小さい正三角形が
今度は4つできます。

この底辺以外の辺の和とAB+ACの長さが等しくなります。
これを延々に続けると。。。無限の三角形が出来上がり、
三角形ABCの辺BCと同じになります。
つまり、AB+AC=BC
1 + 1 = 1
と なるわけです。
















