”誕生日のパラダクス”〜直感で数学を考えると馬鹿を見る？

サッカーの試合の後

　サッカーの練習試合で､互いのチームは不思議と気が合ったし､ゲーム内容も素晴らしかった。
　その試合で笛を吹いた審判が､互いのチームのフェアで真摯なプレーに痛く感動し､互いのチームを食事に誘った。

　”君たちは紳士中の紳士だ。今日の試合は私が笛を吹いた試合の中でもベストゲームだったよ。今日は私のおごりだ。心おきなく食べて､そして呑んでくれ”

　選手のある一人が呟いた。
　”多分､年代が近いからでしょう。皆まだ20代そこそこだから､不思議とウマが合うんですよ”
　
　実際に､11人×2=22人の年齢を確認すると､20歳が半数以上を占めた。
　年齢を1人1人確認する内に､不思議と誕生日の話になる。

　審判はある事に気がついた。
　”でも､私を含め､同じ誕生日の人が全くいないというのも不思議だな？そんなもんかな”

　選手の一人は叫んだ。
　”ええ？でもそんなもんでしょ。逆に､同じ誕生日の人がいる事自体が奇跡ですよ。ワールドカップで日本がベスト4に入るようなもんでしょ？”

　審判は首を横に振る。
　”それがね､私も含めた23人のうち､2人以上の誕生日が同じである確率は､実を言うと驚かれそうだが､五分五分よりやや大きい位なんだよ”

　選手の一人は叫んだ。
　”エエエーっ！そんなに大きな確率で､同じ誕生日が存在するんですか？”

誕生日のパラダクス

　そのカラクリはこうである。
　ある日が誕生日になる確率を1/365で全く等しいと仮定する。
　しかし実際には､1年の中でも確率の高い日や低い日があり､国によってもバラバラである。それらの要素を考慮に入れても､”半々”の確率は変わらない。やはり驚くような結果になるのだ。
　つまり､数学を直感で考えるとアホを見る。数学は数学の論理で考えるべきなんですよ。

　各選手にとっての確率は､1/365で独立してるものとする。当然の事だが､同じ誕生日の者だけを集めたら､確率は1(=100%)になる。
　さてと､23人が同じ誕生日である確率を求める訳だが､ここでは数学的背理法を使い､23人の誕生日が全て違う確率を求めた方が､ずっとずっと簡単だ。
　確率という計算規則では､1からその確率を順に引いていけば､その逆の確率を得る事が出来ます。
　つまり､ある事が起こらない確率は､1からある出来事が起きる確率を引いた確率ですね。
　これこそが確率の計算原則であり､それには､ピッチに1人1人ずつ入ってくる(誕生日が異なる)確率を掛け合わせればいい。

　先ず1人目の誕生日が他の人と違う確率は､当然ですが､1(=100%)です。2人目が入って来た時､その人の誕生日が1人目と異なる確率は､これも当然ですが､365日から1日を引いて､364/365ですね。
　3人目も同様に､最初の2人とは誕生日が違うので､365日から2日を引いた確率を掛けると､3人の誕生日が同じでない確率は､(364/365)×(363/365)。
　4人目も同様に､最初の3人とは誕生日が違うので､4人の誕生日が同じでない確率は､(364/365)×(363/365)×(362/365)。
　ここまで来れば､あるパターンが見えてきます。つまり､k人が入って来た時､k人の誕生日が全て異なる確率P(k)は､P(k)=(364/365)×(363/365)×(362/365)×･･･×((365−k+1)/365)となります。
　
　ここでは､k=23人ですから､実際に計算すると､23人の誕生日が全て違う確率は､P(23)=0.492703となり､そうでない確率､つまり､少なくとも2人の誕生日が同じ確率は､1−P(23)=1−0.492703=0.507297となります。
　これは､1/2より僅かに大きい。つまり､”ほぼ半々”なんですね。
　つまり､ピッチに23人いれば､同じ誕生日が存在する確率は､そうでない確率よりも高いんです。
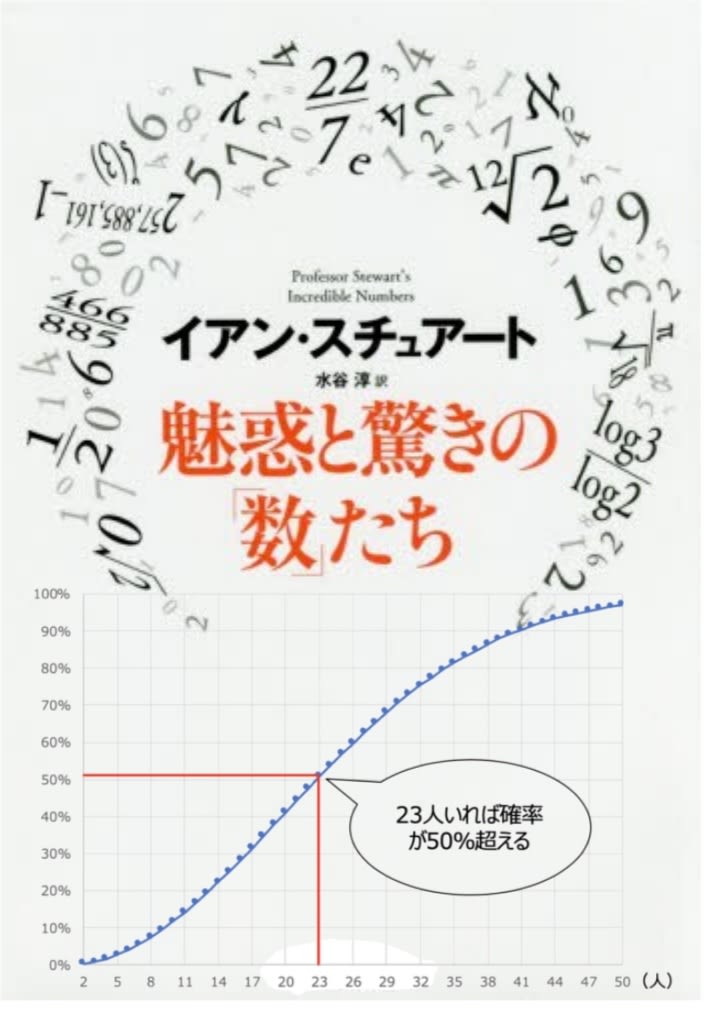
　因みに､k=1から50まででkによって､同じ誕生日である確率”1−P(k)”は､k=23辺りで既に1/2を示してます(イラスト参照)。

　しかし意外なのは､23という数字の小ささですね。脊椎反射系に頼る動物的直感で言えば､”偶然の一致”の確率が半々になるには､もっともっと大きな数が必要だと思えるんですが。
　しかし､この直感は間違ってました。これは1人増える毎に､1より徐々に小さくなる確率が掛け合わされる事で､一致の確率が予想よりも速く小さくなるからです。

　この人数の少なさに驚く理由は､もう一つある。
　”誰か1人が､貴方と同じ誕生日である確率が1/2より大きくなるには何人必要か？”という問題と混同するからでもあろうか。
　この問題の方が少し簡単だ。1人ずつ増やしていき､誰も貴方と同じ誕生日でない確率を計算すればいい。
　つまり､1人増やす毎に貴方の誕生日と違ってる確率は､常に364/365ですね。故に､k人いれば､(364/365)×･･･×(364/365)=(364/365)ᵏとなる。
　この場合､364/365<1より､掛け合わせる程に小さくはなるが､その下がり方は先程の確率よりもずっとゆっくりです。
　実際に､1/2より小さくなるのは､(364/365)²⁵³=0.499523より､k=253となる。
　つまり､この問題で驚くのは､この253という数があまりにも大きい事だろうか。

最後に〜数学のパラダクス

　審判は満足そうに囁く。　
　”今や数学の世界において､難題とされる予想の証明はその大半が､逆説”パラダクス”から攻め落とすとされる､古来ギリシャ時代から受け継がれてきた”背理法”なんだ。
　昨今の現代数学では､この”批判数学”が主流で､数学の巨人ガウスは､<ケチつけるやり方だ>として背理法を嫌ってたとか”

　選手の1人が呟く。
　”つまり､背理法とは相手の背後を突くカウンターアタックみたいなもんだよね。
　でもこの考え方こそが数学的思考で､経験に頼るアナログ的直感とは違う所なんだろうか”

　もう一人の若者もうなずく。
　”この数学的脳こそが今の時代に重要とされるのも肯けるな。でも経験や勘だけでは､今やサッカーでも通用しないのか”

　審判はクビを振る。
　”イイヤ､そうでもないさ。
　動物的直感は必要だよ。閃きって奴だが､それを養うには､数学的洞察力や幾何的観察眼を鍛える必要があるし､それ以外にも色んな経験をする必要がある”

　ある選手は叫んだ。
　”アナログと数学的思考との融合が大切なんだろうか？”
　
　しかし､大半の若者は首を傾げたままだった。
　実際に数学とは神秘で奇怪な学問でもある。いきなり理解しろってのも無理な話ではある。

　以上､数学的思考のパラダクスの話題でした。