”魔法のモノサシ”に見る､多様体とテンソルのお話(更新)〜ナッシュJrの驚異”補足編”

　｢ナッシュJrの驚異(後半)｣では､多様体の”埋め込み”理論について書きました。
　リーマン多様体をユークリッド空間(曲率ゼロの3次元空間)の中へ等長に埋め込んだのが天才ナッシュJrです。が当時､このテーマは未解決問題の1つとされてました。
　この理論の流れとしては､ガウスの曲率→リーマン多様体→ナッシュの埋め込みと､その時代を代表する天才たちの見事な連携をもってして継承されて来ました。

　もし､宇宙に無限に広がる無数の星の分布をリーマン多様体とみなし､ユークリッド空間という曲率ゼロの世界に歪む事なく埋め込めるとしたら？
　つまり､”宇宙の全てを一枚の地図に収める事ができたら・・”これこそがガウスのリーマンの､そしてナッシュの夢でもありました。
　そこで今日は､埋め込み理論には欠かせないリーマン多様体のその基幹を成す計量テンソルについて述べたいと思います。
　というのも､”魔法のモノサシ”と呼ばれるテンソルの本質を知ると知らないとでは､多様体と埋め込み理論を理解する上で､いやもっと大袈裟に言えば､現代数学を理解する上で大きな違いがあるからです(多分)。　　

計量テンソルという魔法のモノサシ

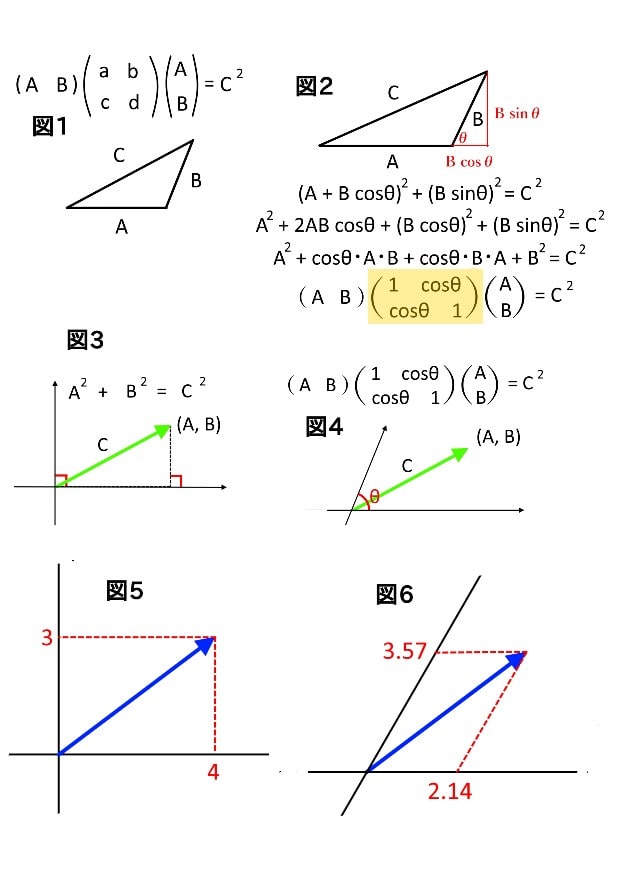
　そこで､”計量テンソル”について､上図(イラスト)を参考にしながら､簡単な例を挙げてわかりやすく進めてきます。
　まず､”ピタゴラスの定理=三平方の定理”(A²+B²=C²ー①)を考えます。これは3辺の長さがA,B,Cの直角三角形が前提ですが､全ての三角形では､4つの係数(a,b,c,d)を使えば､aA²+bAB+cBA+dB²=C²ー②となる事が分っています。これこそが本来のピタゴラスの万能定理とも言えますね。
　因みに､係数(a,b,c,d)を(1行1列,1行2列,2行1列,2行2列)の2×2行列の要素とし､この行列を使って書き直すと､②式は(図1)の様にスッキリとした形となる。一方で､この行列は三角形の辺Cの長さだけではなく､(以下でも述べるが)3辺の長さの関係､即ち”三角形の形を決めてる”とも言える。

　例えば､∠ABの外角をθとすると､(a,b,c,d)=(1,cosθ,cosθ,1)となりますね。これは､(A+Bcosθ)²+(Bcosθ)²=C²を展開し､②式と係数比較すれば明らかです(図2)。
　つまり､ある1つの外角θが判れば､係数a,b,c,dの値が一発で求まる。故に､係数が分かれば､A²+cosθ･A･B+cosθ･B･A+B²=C²の等式がどんな三角形でも成り立つ。更に言えば､ある辺とそれに対応する角度が求まる事で､三角形の形も判る。
　最後でも述べるが､”計量テンソルで距離と角度､つまりベクトルを定義し､多様体上のあらゆる形状を計る事が出来る”とはこういう事である。

　ここで見方を変え､三角形をベクトルに置き換えてみる。つまり､△ABCで(A,B)をベクトル成分と考えれば､辺Cはその大きさとなる(図3)。これは､辺Aと辺Bの長さがベクトルCの成分となってる事が判りますね。
　例えば､XY座標で見れば､X軸とY軸の角度θは∠ABの外角θと一致する。故に､X軸とY軸の角度がθの時､係数a,b,c,dは(a,b,c,d)=(1,cosθ,cosθ,1)となる(図4)。
　つまり､この行列は座標の歪み(傾き)を示し､これを計量テンソルと呼ぶ。例えば､行列=(0,1,1,0)なら直交座標となるし､(1,0.5,0.5,1)ならθ=60度となる。
　そこで､θ=60°の座標で､大きさ5のベクトルを考え､このベクトル成分を座標から読みとれば､(A,B)=(2.14,3.57)がわかる。これをまず①式に当てはめると､2.14²+3.57²≠5²となるが､②式に(a,b,c,d)=(1,0.5,0.5,1)を当てはめると､等式が成立する(図5)。
　この様に計量テンソルさえ判れば､どんな歪んだ(傾きを持つ)座標でもベクトルの成分からその大きさを計算する事ができる。これは､直交座標上の成分(A,B)=(4,3)でも同様で､②式に(a,b,c,d)=(0,1,1,0)を当てはめれば､等式が成立する(図6)。

　以上より､ベクトルの大きさを測るとは､2点間の距離を測る。つまり計量するのと同じで､計量テンソルがわかれば､どんな歪んだ座標でも2点間の距離が正確に計れる。つまり”計量”が可能になる。
　因みに､(2.14,3.57)と(4,3)は角度が違うが故に成分も違うが､実は全く同じベクトルと言える。同様に､(1,0.5,0.5,1)も(0,1,1,0)も(1,cosθ,cosθ,1)としてみれば､全く同じ計量テンソルと言える。
　つまり､ベクトルも計量テンソルも座標変換に応じて自動的にその成分が変換され､②式が常に成立する。故に､テンソルという"座標変換に耐える形式"になってる所が行列とは異なる重要な点だと言えますね。
　以上､｢世界一わかりやすい計量テンソルの話｣から一部抜粋し､計量テンソルの魔法のものさしを大まかに説明しましたが､お解り頂けたでしょうか。

　つまり計量テンソルとは､あらゆる空間(多様体)上の任意の2点間の距離(サイズ)を計る”魔法のモノサシ”といえます。
　このリーマン(が発見した)多様体では空間が伸び縮みし､かつ曲がったりするから､こうしたグニャグニャになった空間の各点にて長さを測る為の”万能のモノサシ”が必要になる。
　計量テンソルは､こうした歪んだ座標変換に耐えうるが故に､距離と角度を定義でき､多様体上のあらゆる形状を計る事が出来るとも言えます。
　因みに､リーマン多様体を数学的に言えば､多様体の各点の近傍が局所的な(曲率ゼロの)ユークリッド空間になってて､全体としては様々な性質をもつ図形を意味する。
　更に､多様体を曲率で分ければ､曲率0のユークリッド幾何学(放物線幾何学)､曲率が負のボヤイ･ロバチェフスキー幾何学(双曲線幾何学)､そして曲率が正のリーマン幾何学(楕円幾何学)と､この3種の幾何学ですが､局所的に見ると殆ど変わらない。我らが住んでる地球も局所的では(曲率0の)ユークリッド的(平面)に見えるが､全体で見ると球面(非ユークリッド)ですよね。
　宇宙は歪んだ空間だと考えられてますが､宇宙全体を見渡すと､想像もつかない様な歪な3次元多様体かもしれないし､意外にも真ん丸かもしれない。でも私達は局所的にしか宇宙を眺める事しか出来ない。
　かつて､ホーエルハーゲン､ブロッケン､インゼルスベルクの3つの山頂からなる巨大な三角測量に基づき､宇宙の謎を解明しようとしたガウスは､真の意味での大天才ですね。

　一方で､”リーマン計量”ですが､(こうした)局所での計量テンソルとも言えます。言い換えれば､”局所での距離の測り方”となる。更に言えば､どんなに歪んだ空間でも局所上での座標はある角度θを持つ座標として定義できる。
　つまり①式は､冒頭で述べたピタゴラスの定理と同様に(dx)²+(dy)²=(ds)²となり､この時のdsは線素(=測地線(最短曲線)を与える素)となる。また､②式はg₁₁(dx)²+g₁₂(dx)(dy)+g₂₁(dy)(dx)+g₂₂(dy)²=(ds)²となり､(g₁₁,g₁₂,g₂₁,g₂₂)は2×2の対称行列(g₁₂=g₂₁)となる。
　故に､2次元平面の直行座標では(0,1,1,0)となり､これは単位行列になってます。
　一般の3次元では [g₁₁ g₁₂ g₁₃]
　　　　　　　　　[g₁₂ g₂₂ g₂₃]
　　　　　　　　　[g₁₃ g₂₃ g₃₃]
の形の3×3行列になるが。更に､n次元でも同様に表現されます。
　これ以上先に進むと､とても難解になるので､ここら辺でヤメにしますが､”ピタゴラスの定理の拡張版”と考えれば､理解しやすいかもです。

リーマン多様体と”井の中の蛙”？？

　最後に､再びリーマン多様体に戻りますが､”井の中の蛙”を例にとって終わりにしたいと思います。

　井の中の蛙は､”井”を知る事ができるのか？
　これは､”井の中の蛙は己をわかる事ができるのか？”という問題でもある。
　己をわかろうとする者は思想に向かう。実際､己をわかろうとする思考の括りが”思想”である。
　そして､自分を”井の中の蛙”に見立てる者は､”井”を知ろうとする思想､つまり､方法論に惹かれる事になる。
　井の中の蛙が”井”を知る為には､空間を内から手探りする他にはない。つまり､これしか無いという意味で､これが方法論となる。

　数学で､この方法論を明示的に主張したものに”リーマン多様体”がある。
　つまり､これは”手探り”の数学でもある。
　”手探り”とは､計量(テンソル)という”記憶”に留めながら､”手探り”の点をシフトしていく。
　そして､空間を構造化するこの作業は､空間を”多様体”に構造化する。しかもこれは､点ごとに”記憶”(計量)を設けるタイプの多様体。
　つまりこれこそが､”リーマン多様体”である。
　こうして井の中の蛙は､”リーマン多様体”を通じて､”井”を知る事となる。

　つまり､己を知るという事は､自分を囲い込む世界を多様体に置き換え､多様体内の各点ごとの記憶(計量)を整理する事で己を手探りに考察するとなろうか。
　一方で､こうした考察する力というのは､己を知る際にも大きな威力を発揮し､これから先の生き方をも示唆してくれる様にも思える。