蘇る天才アーベルのアイデア”その5”〜1824年の論文と解の不可能性(中盤)

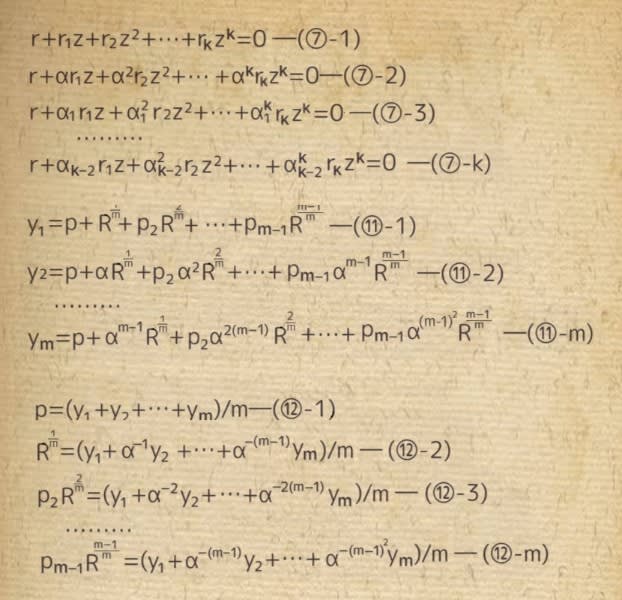
　前回｢その4｣では､アーベルの不可能の証明の第1段階を紹介しましたが､一気に進みすぎたので､今回はその補足として､1つ1つ解説しながら振り返りたいと思います。
　前回とダブる所が多々あるとは思いますが､悪しからずです。

　アーベルの証明には､”解を添加する”という言葉が最初に登場する。
　これは四則演算で閉じた体をFとし､それに新しい要素γを追加した時､Fの元とγの間の四則で閉じた体F₁に拡張する事を”Fにγを添加する”とアーベルは呼んだ。つまり､F₁→F₂→…と膨らみ､Fₖの所で限界が来るとアーベルは予想したのだ。
　結果から言えば､そのkは5となるが､それこそが代数的非可解性の証明の帰着である。

STEP1

　まず証明の第1段階では､一般の5次方程式をy⁵−ay⁴+by³−cy²+dy−e=0―①と書き､これが代数的に可解だったと仮定し､”その解yが係数a,b,c,d,eとそれを含む多重のべき根からなる代数式により表現できる”とアーベルは仮定し､議論を進めていく。
　この時､y=p+p₁･ᵐ√R+p₂･ᵐ√R²+⋯+pₘ₋₁･ᵐ√Rᵐ⁻¹―②と書ける事は”明らかだ”として､m(素数)､R,p,p₁,p₂,…は②の右辺と類似した代数式となる。つまり､”解yは元の5次方程式①の係数a,b,c,d,eのみから出発し､べき根を幾重にも”添加”し､順次得られる代数式(拡張された意味での有理式)の最終段階になる”と､アーベルは結論付けた。
　これもネタバレになるが､②式のmが5になる事の矛盾､つまり､y=p+p₁･⁵√R+p₂･⁵√R²+⋯+p₄･⁵√R⁴の矛盾を導けば､｢不可能の証明｣は成されるのである。

　従って､｢不可能の証明｣の肝は､最初にアーベルが主張した､元の5次方程式①の解が多重べき根(ᵐ√R,ᵐ√R²,⋯,ᵐ√Rᵐ⁻¹)を添加して得られるシンプルな多項式②で表される事にあると言える。
　アーベルが言う様に､ここが理解できれば後の議論はスムーズに展開する訳だが､訳者の山下純一氏が指摘する様に､これだけでは非常に判り難い。故に､アーベルも2年後の論文では､詳しく説明してはいるが､それでも判り難い所がある。

　そこで､山下氏の注釈が入る。
　まず5次方程式の係数a,b,c,d,eの有理式全体をΩ0とおき､Ω0の元(R0,R0’,R0’’,…)の素数の多重べき根(ᵐ⁰√(R0),ᵐ'⁰√(R0’),ᵐ''⁰√(R0’’),…)を添加して得られる(拡張した)有理式全体をΩ1とする。この時､Ω0→Ω1→Ω2→…と次々に拡張し､”代数的可解”の仮定から､最後にはΩkで限界が来る。
　一方で､元の方程式の解yはΩの元であり､最後のΩkの元(Rk,Rk’,Rk’’,…)の多重べき根(ᵐᵏ√(Rk),ᵐ'ᵏ√(Rk’),ᵐ''ᵏ√(Rk’’),…)を添加して得られる有理式全体の元として､解yが表現できる。
　そこでアーベルは､この有理式全体でRkをR､mkをmとおけば､解yがΩ’=Ωk(ᵐ'ᵏ√(Rk’),ᵐ''ᵏ√(Rk’’),…)の元を係数とするᵐ√Rの有理式となると主張した。
　これは､一般には非常に多重化したべき根を含む複雑な代数式(有理式)となる。が更にアーベルは､解yがᵐ√Rの有理式から､②式の様なべき根(ᵐ√R,ᵐ√R²,⋯,ᵐ√Rᵐ⁻¹)の添加による多項式へと簡略化できる事を言いたかったのだ。
　今､これをアーベルの不可能の証明の第1ステップの1番目の結論とする。

STEP2

　この厳密の証明は次回｢その6｣で述べるとして､前回｢その4｣の補足から話を進めたい。
　元の5次方程式①からその解yをべき根(ᵐ√R,ᵐ√R²,⋯,ᵐ√Rᵐ⁻¹)の簡単な多項式②に展開したアーベルだが､””ᵐ√Rはa,b,…,p,p₁,p₂,…の有理式で表せない”と仮定し､”RをR/p₁ᵐで置き換える事でp₁=1とできる”とした。但し､アーベルはp₁≠0とみなしたが､p₁=0の時の議論も必要となる。が､その時も同じ形に持ち込める事が示せる。
　故に､②式は､y=p+ᵐ√R+p₂･ᵐ√R²+⋯+pₘ₋₁･ᵐ√Rᵐ⁻¹―③と書き直せる。
　ここで､①式に③のyを代入して整理すれば､P=q+q₁･ᵐ√R+q₂･ᵐ√R²+⋯+qₘ₋₁･ᵐ√Rᵐ⁻¹―④を得る。但し､但し､q,q₁,q₂,…は､a,b,c,d,e,p,p₂,…及びRの多項式を表す量(文字)とする。

　一方でアーベルは､P=0として④の方程式が成立する為には､”q=0,q₁=0,q₂=0,…,qₘ₋₁=0となる必要がある”とした。
　そこで､ᵐ√R=zとして④に代入すれば､zᵐ−R=0とq+q₁･z+q₂･z²+⋯+qₘ₋₁･zᵐ⁻¹=0―⑤の2つの方程式を得る。
　ここで､q,q₁,q₂,…の全てが0に等しくないと仮定すれば､上の2つの方程式は共通解を持つ必要がある。つまり､これら共通解をk個の解とするk次方程式にて､R,q,q₁,q₂,…,qₘ₋₁の有理式を係数とするものが存在する。
　いま､このk次方程式をr+r₁z+r₂z²+⋯+rₖzᵏ=0―⑥とすると､この方程式の全ての解がzᵐ−R=0の解にもなる事から､これらの解はαᵤzと書ける。但し､αᵤは円周等分方程式であるzᵐ−1=0の解を示す。この時､⑥のzにαᵤzを代入する事で､(⑦-1)~(⑦-k)のk個の連立方程式を得る。が､ここも少し判り難い。
　そこで､山下氏は[原注]として､⑥のzにαᵤ₋₂･zを代入してu番目の式(⑦-u)を得る訳だが､u=1,2,…,kとし､α₋₁=1,α₀=αとする事で､理解がズムーずになる。また､kは⑤式の共通解の個数となる事も判る。
　更に山下氏は､⑤の2つの方程式の左辺にて､｢ユークリッドの互助法｣を行えば､最後に2式の最大公約式が出現し､この”最大公約式こそが⑥式の左辺となる”と説明するが､私にはよく理解できなかった。

　これらK個の方程式から､zを量r,r₁,r₂,⋯,rₖの有理式で表せる。一方で､r,r₁,r₂,⋯,rₖはa,b,c,d,e,R,p,p₂,…の有理式なので､zもまたこれらの有理式となる。が､これは先の仮定に反する。故に､q=0,q₁=0,q₂=0,…,qₘ₋₁=0―⑧となる必要がある。
　これが､不可能の証明の第1ステップの2番目の結論だが､アーベルの議論は少し飛躍がある。が､ここでも山下氏は､[原注]を入れて丁寧に説明してくれる。
　上のk個のk次方程式から､zをr,r₁,r₂,⋯,rₖ,α,α₁,…,αₖ₋₂の有理式で表す事が出来るのは､k個の未知数z,z²,z³,⋯,zᵏからなるk個の1次方程式が作る連立方程式と考える事で理解できる。つまり､k個の未知数を決定する為のk個の1次方程式と見れば､簡単に解ける。即ち､zのべき乗を別々の未知数として考えればいいだけである。
　一方で､最初に､”z=ᵐ√Rがr,r₁,⋯,rₖ,α,α₁,…,αₖ₋₂の有理式ではない”とアーベルが仮定した事を思い出せば､⑧となる事が必要だと判る。

STEP3

　最後に､証明の第1ステップの3番目に入る。
　そこで仮に､q=0,q₁=0,q₂=0,…,qₘ₋₁=0―⑧が成立するとすれば､y=p+ᵐ√R+p₂･ᵐ√R²+⋯+pₘ₋₁･ᵐ√Rᵐ⁻¹―③のᵐ√Rを､ᵐ√R,α･ᵐ√R,α²･ᵐ√R,α³･ᵐ√R,…,αᵐ⁻¹･ᵐ√R―⑨で置き換えて得られるm個のyの値が､元の方程式①を満たすのは明らかである。
　但し､αはαᵐ⁻¹+αᵐ⁻²+…+α+1=0―⑩を満たす”1の虚のm乗根”とする。
　ここでもアーベルは､”明らか”を立て続けに連発するが､αを”1の虚のm乗根”とする時､1,α,α²,α³,…,αᵐ⁻¹が1のm乗根の全体になる事に注意する。
　また､”明らか”となるのは､任意のt∈0,1,2,…,m-1にて､Ω(α)の元:p+(αᵗ･ᵐ√R)+p₂(αᵗ･ᵐ√R)²+⋯+pₘ₋₁(αᵗ･ᵐ√R)ᵐ⁻¹を元の5次方程式①のyに代入すると､④式と同じ形のΩ(α)の元:q+(αᵗ･ᵐ√R)+q₂(αᵗ･ᵐ√R)²+⋯+qₘ₋₁(αᵗ･ᵐ√R)ᵐ⁻¹が得られる為である。ここで､先の⑧の仮定(q=0,q₁=0,…,qₘ₋₁=0)により､これは0となる。故に､④式が①を満たすのは”明らか”となる。

　一方でアーベルは､これらのyは全て異なる事も判るとし､仮にそうでないとすると､方程式P=0と同じ形の方程式が得られるが､STEP2で見た様に､この方程式からは矛盾した結果が得られる。つまり､”mは5より大きくなる事はない”と主張する。
　従って､(⑪-1)~(⑪-m)の様に､y₁,y₂,…,yₘに関するm個の連立方程式を作ると､元の5次方程式①の解をy₁,y₂,y₃,y₄,y₅とおく事が出来るとした。
　アーベルは更に､これらm個の連立方程式から､(⑫-1)~(⑫-m)のm個の方程式を”簡単に得られる”と言う。
　確かに､⑪のm個の方程式を順に足せば､(⑫-1)を得る。また､(⑪-1)~(⑪-m)をそれぞれ1,α⁻¹,α⁻²,α⁻³,…,α⁻⁽ᵐ⁻¹⁾倍して加えると､(⑫-2)が得られ､同様に､(⑪-1)~(⑪-m)をそれぞれ1,α⁻ᵗ,α⁻²ᵗ,α⁻³ᵗ,…,α⁻⁽ᵐ⁻¹⁾ᵗ倍して加えれば､(⑫-(t+1))が得られる。

　ここでアーベルは､”これより､p,p₂,…,pₘ₋₁,R,ᵐ√Rは元の5次方程式の解の有理式となる事が判る”と結論づけた。
　そこで､例えば､Rについて考える。
　いま､R=S+ⁿ√v+S₂･ⁿ√v²+…+Sₙ₋₁･ⁿ√vⁿ⁻¹―⑬とする。これを上のSTEP2でやった様に､yの時と同じ方法で処理すれば､ⁿ√v,v,S,S₂,…がRの異なる値全体の有理式となり､Rの異なる値は全てy₁,y₂,…の有理式となるので､ⁿ√v,v,S,S₂,…もまた､y₁,y₂,…の有理式となる。
　この論法を更に推し進める事で､(③式の様に)yを表す為に必要な全てのべき根ᵐ√R,ᵐ√R²,…,ᵐ√Rᵐ⁻¹が､最初の方程式①の解y₁,y₂,…の有理式となる事が示せる。

　アーベルは”これが判れば､証明を完了する事はそこまで難しくはない”として､証明の第1段階を終える訳だが､これ以降の第2段階では､元の5次方程式の5個の”解の置換”こそが肝となる。　
　因みに､⑦と⑪と⑫の連立方程式は敢えて書かなかったんですが､上図を参照して下さい。